강의 동영상 Lecture 5: Neural Networks
슬라이드 및 이미지 참고 slides

Feature Transform

선형분류는 매우 간단하고 이해하기 쉽지만, geometric viewpoint나 visual viewpoint에서 볼 수 있듯이 한계가 있다.

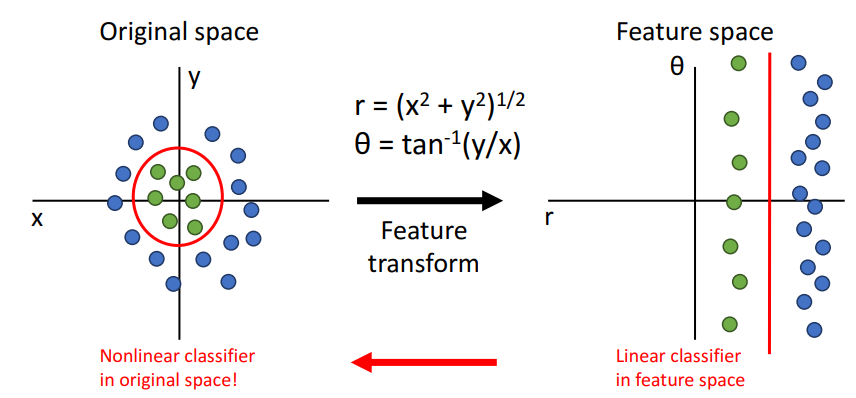
그래서 feature transform을 통해 분류에 더 적합하게 변환한다.

Color Histogram

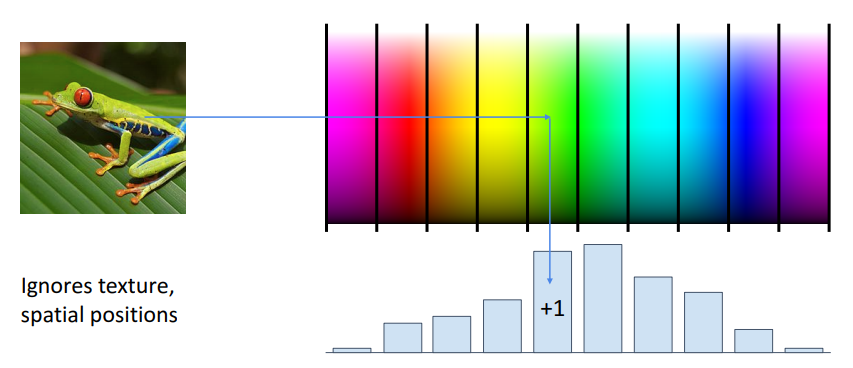
대표적인 예시가 컬러 히스토그램인데, 이미지에 대한 공간정보, 질감, 위치 등을 다 제외하고 단순히 이미지의 색상을 가지고 히스토그램을 만들어 분석한 것이다. 이 방식을 사용하면 이미지 속의 객체의 각도나 위치 등이 달라지는 문제를 피할 수 있다.

Histogram of Oriented Gradients

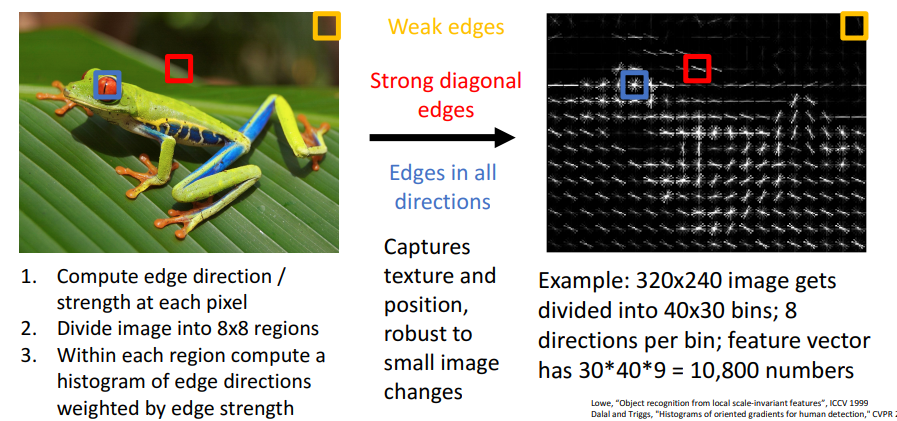
컬러히스토그램 말고도 Hog 또한 feature transform의 분야 중 하나이다. 이 방식은 이미지에서 local edge만 남기고, edge를 이용해서 이미지를 분석한다. 위 이미지를 보면 눈 주위의 영역(파란색박스)을 보면 상당히 강한 edge가 있고, 노란색박스영역을 보면 매우 흐릿한 배경이기 때문에 edge 정보가 거의 없다는 것을 알 수 있다. 이 방식은 2000년대 중후반까지는 object detection에서 많이 사용되었다.

color histogram, HoG 모두 어떤 feature를 어떻게 추출할 것인가 등 구현에 있어 많은 노력이 필요하였다. 그래서 Bag of Words라는 Date-Driven이라는 방식이 새롭게 나왔다.

Bag of Words: Date-Driven

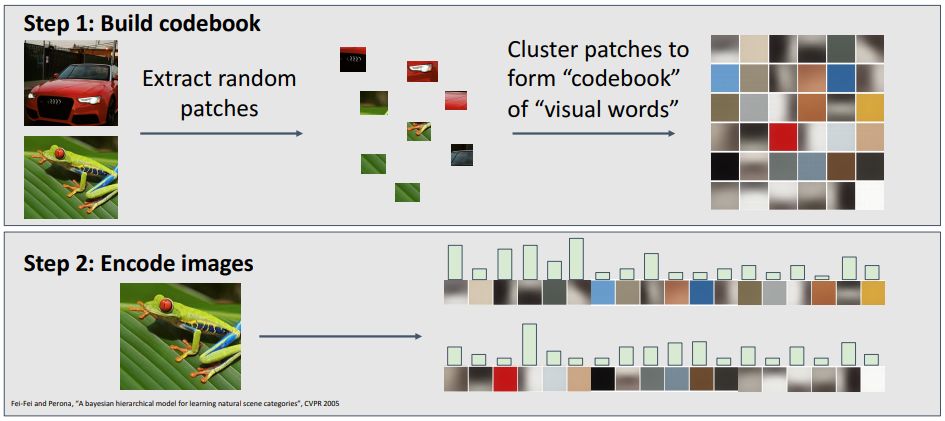
다양한 스케일과 크기의 patch들을 무작위로 추출한 후, 각 patch들을 클러스터링하여 이미지에 어떤 종류의 특징이 나타나는지 나타낼 수 있는 visual word set인 code book을 얻을 수 있다. 그렇게 학습된 code book을 사용하여 입력된 이미지에 대해 visual word가 얼마나 많이 나타나는지를 히스토그램으로 표현하여 이미지를 분석한다.

Image Features

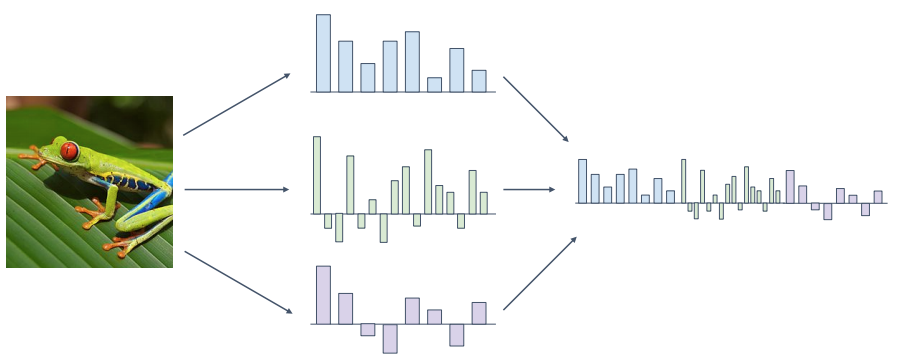
이미지에서 컬러히스토그램이나 HoG 등의 방식으로 여러개의 feature vector를 만든 후 이를 통합하여 사용하는 방식도 있다. 이 방식으로 2011년의 ImageNet challenge우승자는 이 방식을 채택하여 우승하기도 하였다.

Image Features vs Neural Networks

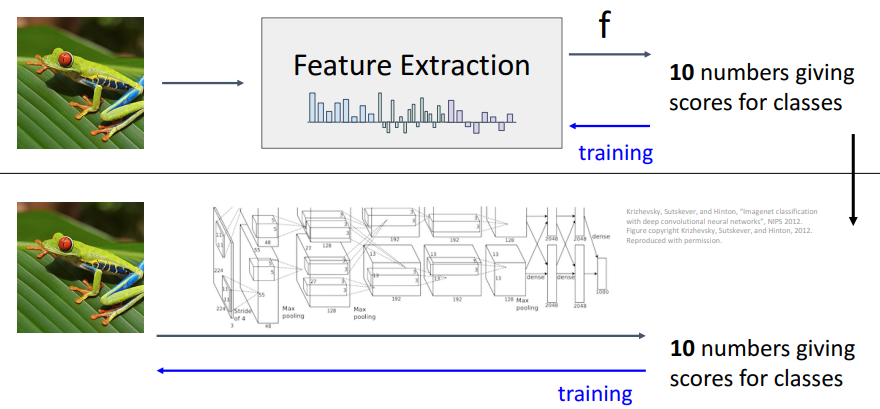
지금까지 언급한 방식들 모두 사람이 모든 과정에 개입했어야 했다. 하지만 Neural Network는 feature representation조차 스스로 학습해나가는 end-to-end방식의 모델이 가능해졌다.

Neural Networks

Neural Network는 linear classifier를 적층해서 구성하며, 대부분의 신경망 모델을 표현할 때, bias항은 관습적으로 생략한다고 한다.

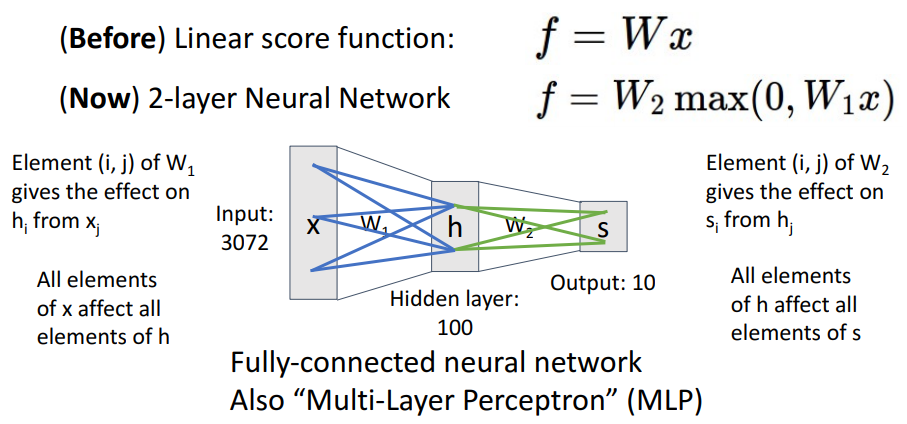
신경망 모델에서는 이전 레이어의 요소가 다음 레이어의 요소에 영향을 미치는 것을 알 수 있다. 이렇게 모두 연결되어 있는 특성 때문에 2-layer Neural Network는 fully-connected network 또는 MLP(Multi-Layered Perceptron)라고도 불린다.

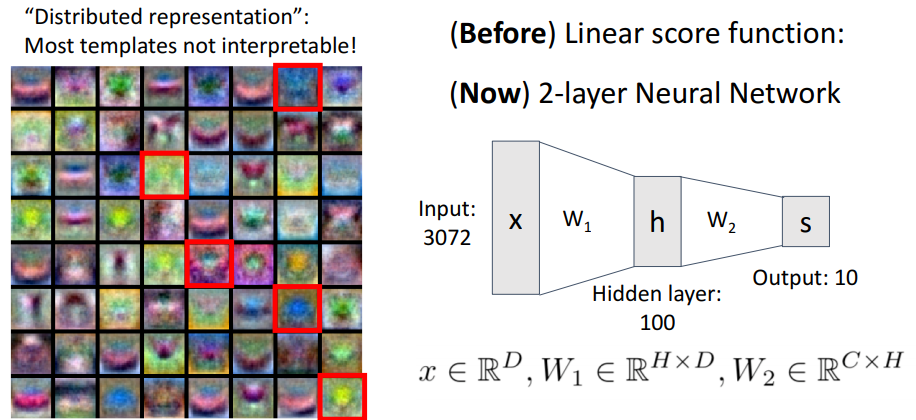
카테고리당 1개의 템플릿만을 만들어 내는 것이 아닌 첫번째에서 각각의 weight마다 템플릿을 만들어내고, 두번째 레이어에서는 이전에 만든 템플릿을 재조합해서 class score를 만들어낸다. 즉 여러개의 템플릿의 조합으로 class를 표현한다고 해서 Distributed Representation(분산 표현)이라고 부르기도 한다.

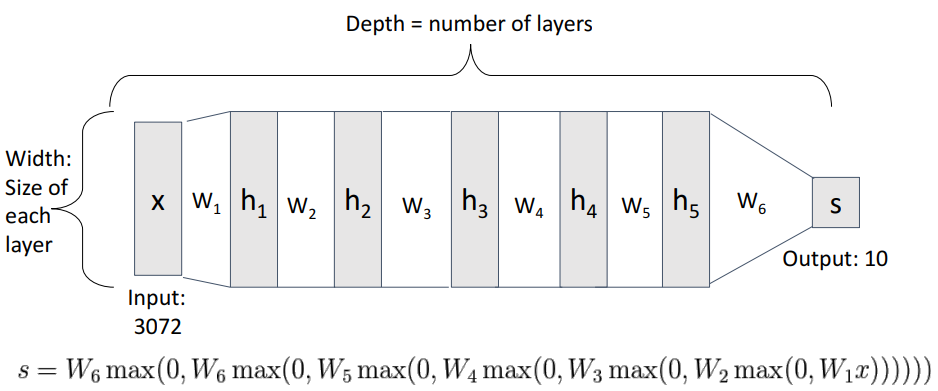
신경망 모델에서 depth는 layer 수를 뜻하며, width는 각 layer의 크기를 말한다.
그리고 s를 만들어낼 때 사용하는 max는 activation function인 'relu'를 나타내는데,

activation function

신경망 모델에서 activation function을 적용하지 않으면 어떻게 될까? 위 수식의 max에서 답을 알 수 있다. 만약 max가 없다면 식은 $f=W_{2}W_{1}x$ 이렇게 표현될 것이다. 이는 그저 또 하나의 선형함수가 된다. 즉 지금까지 다뤄왔던 것들과 다를게 없게 되는 것이다. 이러한 max를 activation function(활성함수)이라 부르고 여기에는 다양한 종류의 함수들이 존재한다.

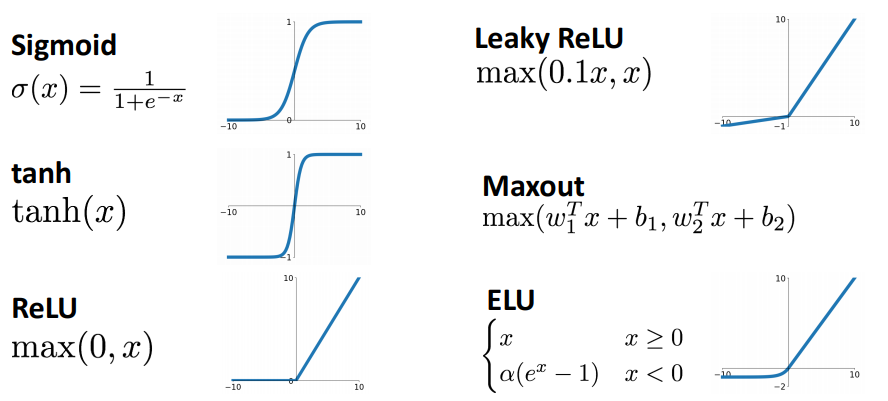
현재는 대부분의 문제에서 relu가 좋은 선택이 된다.

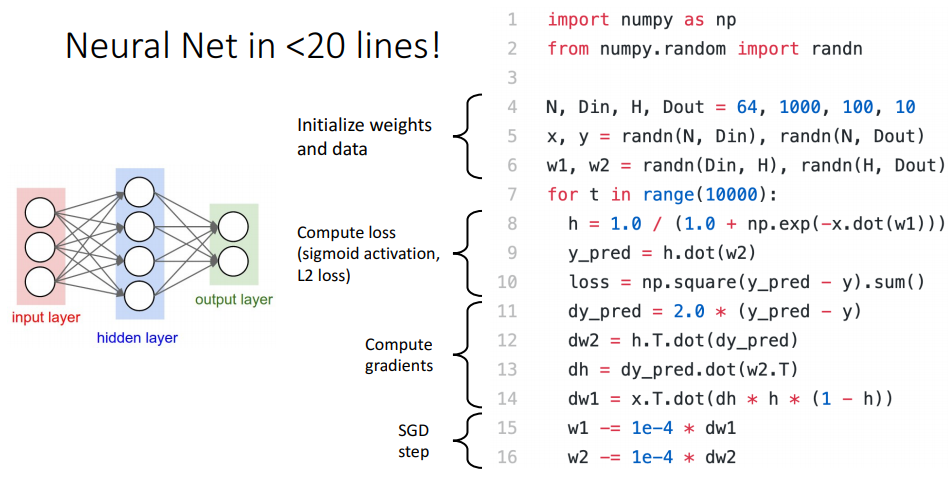
python code로 나타내면 위와 같다.

Neuron

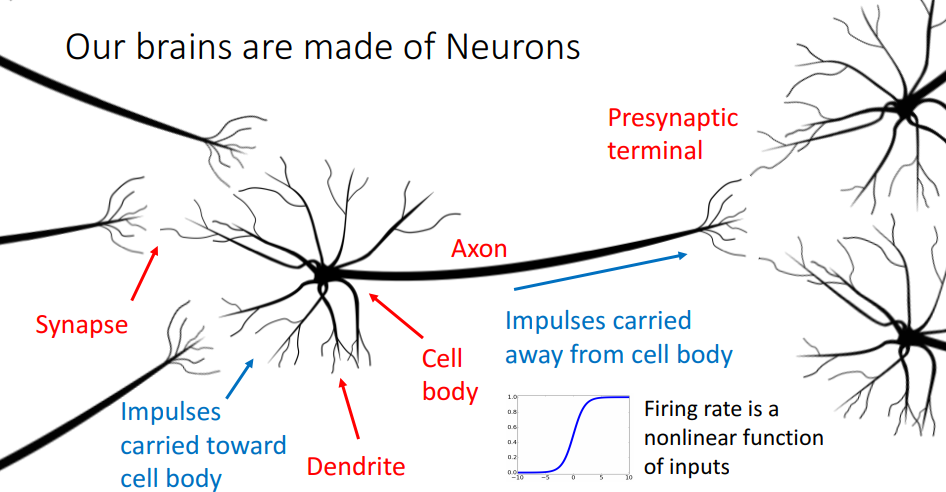
각가의 신경세포는 축삭돌기(axon)라고 불리는 긴 단자를 가지고 있는데 이 축삭돌기를 통해 다른 세포들과 연결되어 전기자극을 보내며 거대한 네트워크를 구성하게 된다.

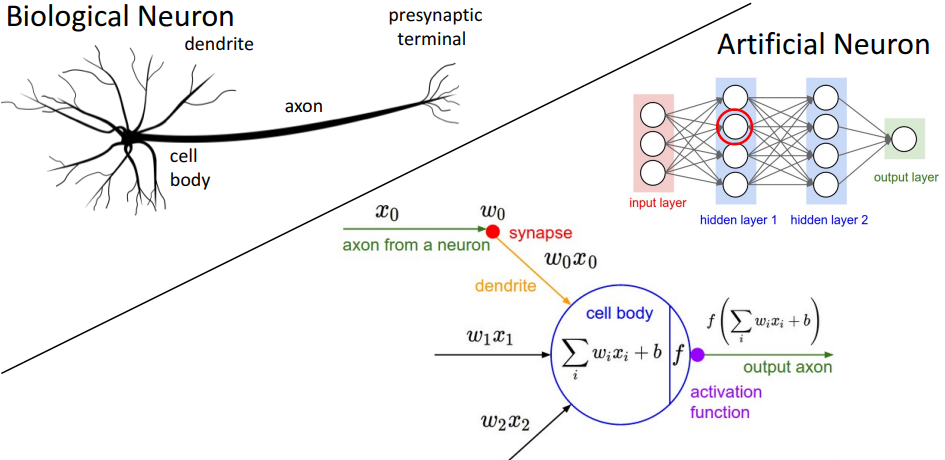
생물학적인 신경세포에서 착안하여, 인공뉴런 또한 비슷한 형태를 띄고 있다. 각 가중치들에 의해 계산된 값을 활성함수를 통과시켜 다음으로 넘기는 방식이다.

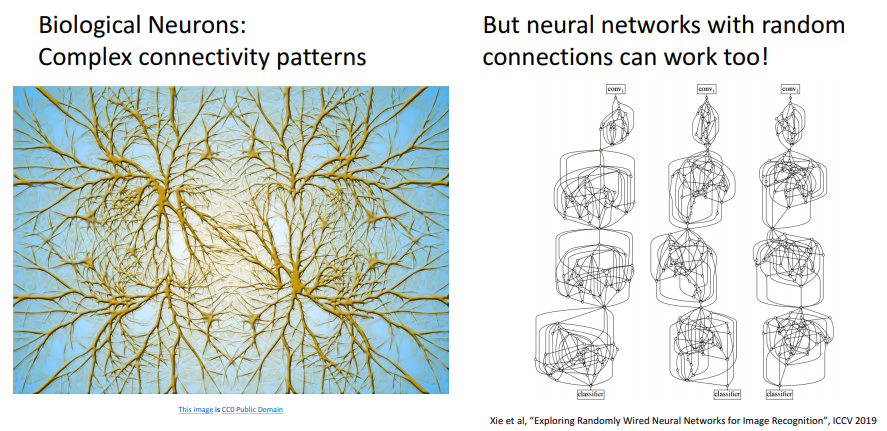
생물학적 뉴런이 복잡한 패턴을 가지고 연산을 하는 데, 랜덤으로 연결된 인공신경망도 효과가 있었다. 또한, 실제 뉴런과 인공뉴런과는 많은 차이가 존재한다.

• Dentride(수상돌기)는 복잡한 비선형 계산을 수행할 수 있다.
• synapse는 하나의 weight가 아닌 복잡한 비선형 동적 시스템이다.
• activation function을 통해 얻은 rate code가 적합하지 않을 수 있다.

그러므로 실제 뉴런과 neural network는 많은 차이가 존재하기 때문에, 실제 뉴런을 단순ㄴ화해서 생각하는 것이지 완벽히 묘사하는 것은 아니다.

Space Warping

입력공간을 뒤틀어 x1과 x2를 가진 입력공간을 가지고 다른 특징 공간으로 변형시키는 것이다. 그리고 우리가 선형변환을 가지고 있는 경우, 우리의 2차원 숨겨진 유닛의 2차원에 대해 h1과 h2를 좌표화한다. 기존의 feature transform 방식은 linear transform이라서 여전히 선형적으로 분리가 가능해 보이지 않는다. 하지만 relu를 통해 space warping해보면 region space가 위와 같이 나타나게 되고, 위 데이터 포인트를 보면 non-linear하게 배치된 데이터도 적절히 분리할 수 있게 된다.

hidden layer

hidden layer를 증가시킨다면 그만큼 더 많은 line을 그어 구분하게 된다. 이는 feature space상에서 훨씬 더 복잡한 묘사를 통해 선형적으로 분리가 가능해질 것이며, 이것은 input space에서 훨씬 더 복잡한 비선형 결정 경계로서 표현될 것이다.

하지만 hidden layer를 증가시켜서 다 분리해낸다면 overfitting의 문제를 생각해볼 수 있다. 그렇다고 해서 hidden layer를 줄이는 것으로 문제를 해결하는 것보다, 위 그림에서 L2를 사용한 것처럼 reqularizer로 처리해야 한다.

Universal Approximation

하나의 hidden layer를 가진 신경망 모델은 $f:R^{N}→R^{M}$ 형태의 함수로 근사하여 표현이 가능한데, 이것을 Universal Approximation이라고 한다.

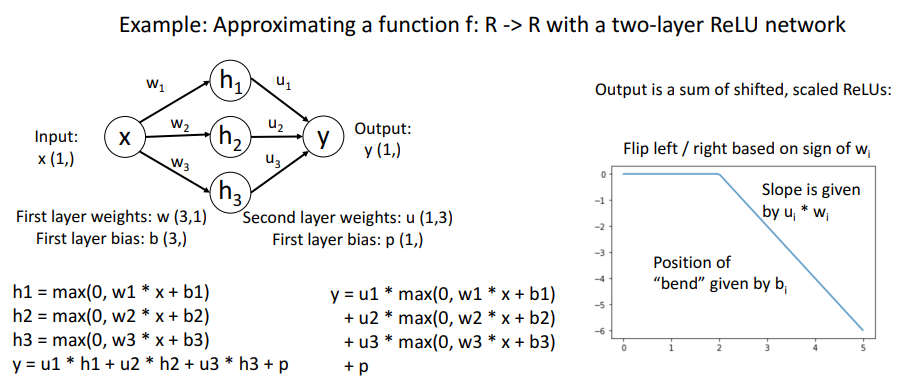
위는 2-layer ReLU network의 형태를 표현한 것이다.
좌측 하단의 y는 hidden layer value의 linear combination형태로 나타낼 수 있다.
또 다른 형태로 y를 나타내자면, 3개의 다른 terms들로 분해될 수 있고, 각각의 terms들이 shift된 relu의 합이다.

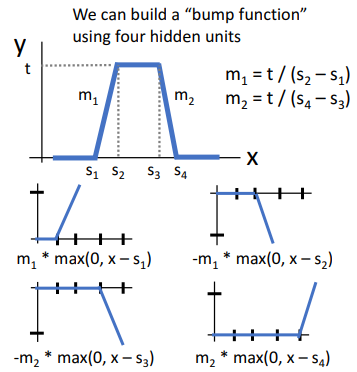
임의로 shift되고 scale된 4개의 relu를 모아서 위와 같은 bump function을 만들 수 있는데, 이 bump function을 이용하면 어떤 함수든 근사할 수 있으며, 그래서 2-layer neural network가 Universal Approximation이 가능하다고 하는 것이다.

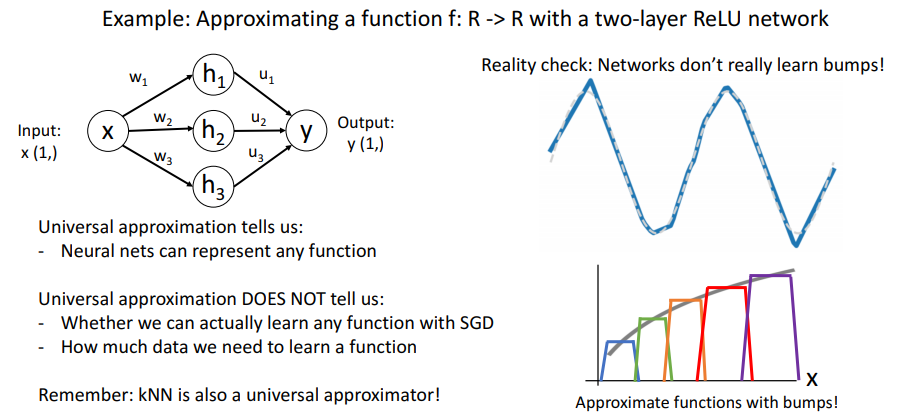
하지만 Neural Network로 Universal Approximzation이 가능하다고 해서 Neural Network가 Bump Function 자체를 학습하는 것이라고 볼 수는 없다. 또한 Universal Approximation은 Neural Network가 어떤 함수든지 표현이 가능하다는 사실만 알려줄 뿐, SGD를 사용했을 때도 어떤 함수든지 표현이 가능하다는 사실을 알려주는 것도 아니고, 학습에 데이터가 얼마나 필요하다는 사실도 알려주지 않는다.
그래서 단순히 Universal Approximation이 가능하다고 해서 Neural Network가 최고의 모델이라는 주장을 해서는 안된다. 낮은 성능을 보여주는 KNN 또한 Universal Approximation이 가능하다.

Universal Approximation 실험 참고

Convex Function

어떤 함수에서 임의의 두 점을 잇는 선분을 그었을 때, 항상 두 점 사의에 위치한 점들이 모두 선분 아래에 위치한다면 그 함수를 Convex Function이라고 한다. 즉 위의 부등호 조건을 만족한다면 말이다.

위 조건을 만족시키지 못하는 cos(x)는 convex function이 아니다.

고차원 공간에서의 Convex Function은 bowl shape을 그리는 함수를 지칭하며, Convex Function은 기울기를 따라 내려간다면 간단히 global minimum에 도달할 수 있다. 그래서 Convex Function에서는 초기화에 따른 영향도 덜하다.

Linear 모델에서는 항상 convex 함수가 Global Minimum에 도달하는 것이 이론적으로 보장되어 있지만, Neural Network에서는 그러한 이론적 뒷받침이 존재하지 않는다. 그래서 일부 경우에는 Linear 모델이 더 선호되기도 한다.

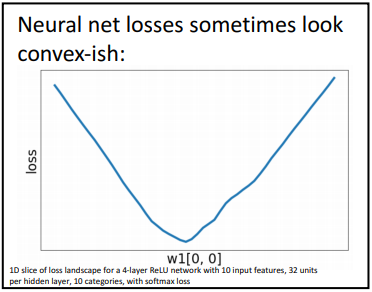
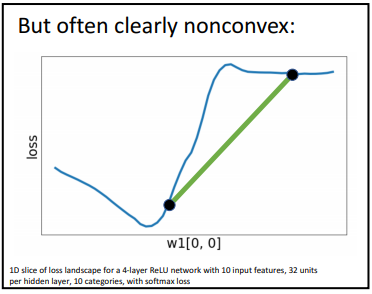
Neural Network에서는 Convex Function임을 확인하고 싶을 때, 고차원의 loss에서 Weight Vector W에서 1개의 원소에 해당하는 slice를 떠서 확인하는데, slice가 Convex를 이룰 때도 있지만, 아닐 때도 있다.

그래서 대부분의 Neural Network에서는 nonconvex를 이루는 데이터에 대해서도 optimization 방안이 필요하다.

Summary

1. linear classifier가 feature transform을 통해 non-linear decision boundary를 linear하게 구분하는 방법
2. inear classifier와 2-layer neural network를 비교하여 살펴봄으로써 왜 neural network가 powerful한가.
3. space warping, universal appriximation, non-convex을 통해 neaural network system이 어떠한 특성을 갖는지 살펴보았다.