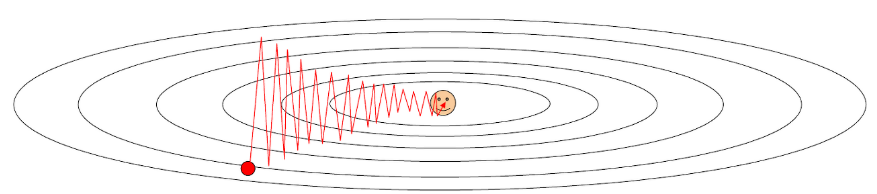
Optimization
사전적 의미 : 최적화, 가장 효과적인 상태
사전적 의미처럼 optimization은 최적화를 시키는 것으로, loss가 0인 지점을 찾아나가는 것이다.
Random Search
임의로 가중치 W를 선택하여 이 가중치에 대한 loss를 계산하는 것.
- 실제로는 사용되지 않는다.
Numerical Gradient
- Follow the slope
- 다차원에서 gradient는 편미분(partial derivatives)값을 갖는 벡터

-
- 현재 W에 대해 loss를 계산한다.
- W의 각 차원에서 h만큼 움직여서 그때 loss를 계산한다.
- 현재 loss와 h만큼 움직인 loss의 차이를 구하여 h로 나눠서 gradient를 구한다.
- 위 방법을 W의 모든 차원에 대해서 반복한다.
- h가 아주 작은 값이라는 가정하에 이 gradient를 추정한 것
- 각 차원에 대해 반복하다보니 계산이 오래 걸려 실제로 사용하진 않는다.
- approximate(근사치인), slow, easy to write
def eval_numerical_gradient(f, x):
fx = f(x)
grad = np.zeros(x.shape) # x차원만큼 gradient를 담기위해 0으로 초기화
h = 0.00001 # 한발자국 움직일 h의 크기를 정해준다.
# np.nditer를 이용해 iterater객체를 만듬
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not il.finished:
ix = it.multi_index # 현재 index를 ix에 저장
old_value = x[ix] # 현재 x값을 old_value에 저장
x[ix] = old_value + h # x[ix]에 x축에서 h만큼 이동한 값을 저장
fxh = f(x) # x+h일 때, 함수값을 구해서 fxh에 저장
x[ix] = old_value # 앞서 old_value에 저장했던 기존x좌표를 보관
grad[ix] = (fxh-fx)/h # grad배열이 현재 index에 구한 gradient값을 저장
it.iternext() # 다음 차원으로 넘어가면서 이를 반복.
return grad # grad라는 배열을 통해 각 차원에 대한 gradient를 구할 수 있다.np.nditer 참고
https://numpy.org/doc/stable/reference/arrays.nditer.html#arrays-nditer
https://numpy.org/doc/stable/reference/generated/numpy.nditer.html
Analytical
- 해석적, 미분
- loss function을 W에 대해서 미분한 값을 구하고자 한다.
- exact(정확한), fast, error-prone(에러가 발생하기 쉬운)
- Analytic Gradient를 개발했을때에는 실제 모델에 적용하기 전에 Numeric Gradient를 사용해 제대로 구현되었는지 확인하는 Gradient Check라는 것을 해야한다.
Gradient Descent 경사하강법
- weight gradient가 증가하는 반대방향으로 움직여서 최소값을 찾아간다.
Vanilla Gradient Descent
gradient의 반대방향으로 파라미터를 업데이트하는 것
w = initialize_weights() # W(weight)를 초기화, 어떻게 초기화하냐에 따라 결과나 과정이 달라짐
for t in range(num_steps):
dw = compute_gradient(loss_fn, data, w) #
w -= learning_rate * dw- dw : gradient를 계산한 결과값
- num_steps : Gradient를 활용해 더 나은 W를 찾아나가는 step을 몇 번이나 수행할지. step 횟수와 학습 소요 시간은 비례
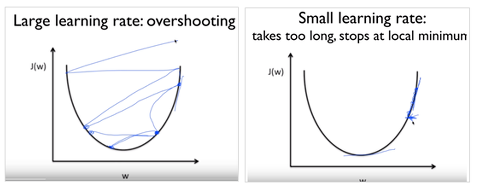
- learning_rate : 한 번의 step에서 이동할 거리. Learning rate가 높으면 최적의 W까지 더 적은 횟수의 step으로 도달 가능하지만 최적의 W를 지나쳐버리는 overshoot 문제가 생길 수 있고, 반대로 learning rate가 낮으면 정교하지만 더 오래 걸린다.
- 앞에 -가 붙는 것은 만약 음의 기울기(\모양)값이면 기울기가 0인 지점(오른쪽 그래프에서 x축이 가장 낮은 지점)으로 가려면 +방향으로 가야하고, 양의 기울기(/모양)이면 기울기가 0인 지점으로 가려면 - 방향으로 가야하기 때문에, 즉 반대 방향으로 가기에 -를 붙여준다.
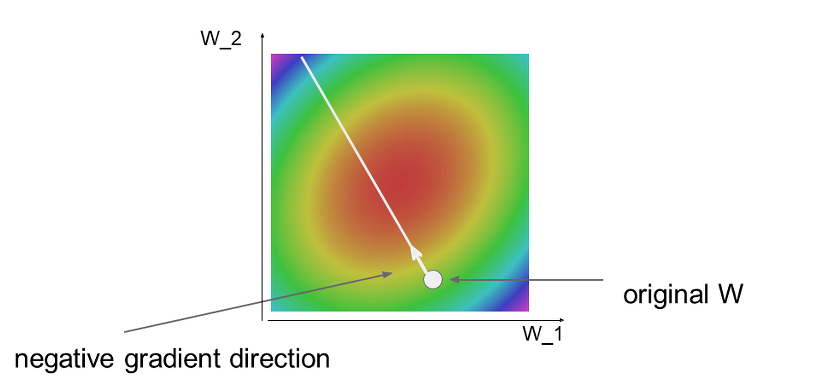
- 그래서 우리는 임의의 w위치에서 가운데인 빨간색 지점으로 가는 것, 즉 기울기가 0에 가까운 지점으로 가는 것이 목표이다.
Stochastic Gradient Descent(SGD)
- 이전에는 N을 한번에 다 올려서 계산했기 때문에 W가 업데이트 될 때마다 처음부터 끝까지 계산을 해야했다. 만약 N이 수천만개라면 매우 느리다. 그래서 SGD를 많이 사용한다.
- SGD는 minibatch를 이용하여 데이터 갯수를 잘라서 사용하는 것이다.
- 전체 학습 데이터를 사용하는 것이 아닌 일부분을 사용하여 gradient를 계산한다.
- 일반적인 Minibatch 사이즈는 32, 64, 128, 256, 512 처럼 2의 승수의 학습데이터를 사용한다.
- 보통 이 사이즈는 gpu의 메모리에 맞게 설정하는 것이 일반적이다.
- SGD에서는 표본 데이터를 가지고 Gradient와 Loss를 구하기에 표본 데이터의 분포가 전체 데이터의 분포와 최대한 유사하도록 표본을 선정해야 한다.
w = initialize_weights()
for t in range(num_steps):
minibatch = sample_data(data, batch_size)
dw = compute_gradient(loss_fn, minibatch, w)
w -= learning_rate * dw- batch size : minibatch의 크기, GPU의 메모리 크기가 허용하는 한, 최대한 크게 잡는 것이 좋다.
- Data sampling : 데이터를 어떻게 선정할 것이냐
Problems with SGD
What if loss changes quickly in one direction and slowly in another?
loss가 한 방향으로 빠르게 변하고 다른 방향으로 천천히 변하면 어떻게 될까?
What does gradient descent do?
경사 하강은 어떤 작용을 합니까?
얕은 치수를 따라 매우 느린 진행, 가파른 방향을 따라 조금씩 움직인다.
Gradient Descent가 지그재그를 그리며 진행되어 더 많은 step이 소요된다는 점이다. 이 때문에 SGD는 Full Batch보다 Overshoot문제에도 더 취약하다.
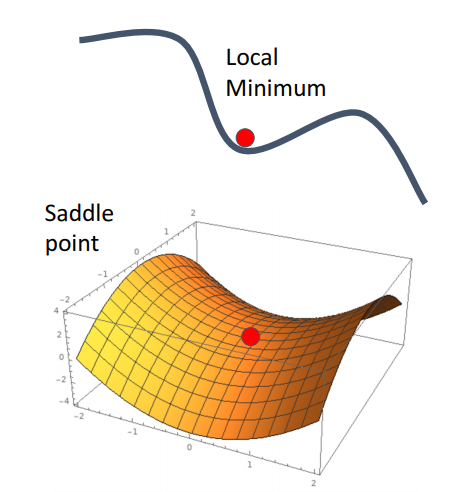
What if the loss function has a local minimum or saddle point?
loss 함수에 국소 최소점 또는 안장 포인트가 있는 경우 어떻게 됩니까?
경사가 0이고, 경사 하강이 고착된다.
Local Minimum에 빠질 위험이 높으며 고차원의 데이터에서는 gradient가 0인 saddle point에 위치해서 학습이 크게 지연될 수 있다.
SGD는 애초에 일부 데이터로만 학습을 진행하기에 Loss Function에서의 W의 궤적이 항상 Loss의 기울기를 따르는 것이 아니라 거꾸로 돌아가기도 하는 등의 노이즈가 끼는 경우가 많다.
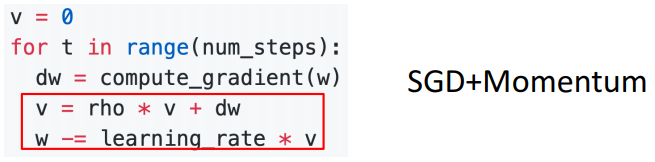
SGD + Momentum
gradient가 오직 속도(velocity)에만 직접적으로 영향을 주고 속도가 위치값(position)에 영향을 줄 것을 제안하고 있다.
- : 얼마나 momentum(가속도)을 줄 것인지에 대한 momentum term으로서, 보통 0.9 정도의 값을 사용
- : 위치
- : 속도 벡터
- 과거에 얼마나 이동했는지에 대한 이동 항 v를 기억하고, 새로운 이동항을 구할 경우 과거에 이동했던 정도에 관성항만큼 곱해준 후 Gradient을 이용한 이동 step 항을 더해준다.
- 자주 이동하는 방향에 관성이 걸리게 되고, 진동을 하더라도 중앙으로 가는 방향에 힘을 얻기 때문에 SGD에 비해 상대적으로 빠르게 이동할 수 있다.
# SGD
for t in range(num_steps):
dw = compute_gradient(loss_fn, data, w) #
w -= learning_rate * dw
# SGD + Momentum
v = 0
for t in range(num_steps):
dw = compute_gradient(w)
v = rho * v + dw
w -= learning_rate * v
# rho : friction 혹은 decay rate라고 부른다.1. SGD + Momentum
v = 0
for t in range(num_steps):
dw = compute_gradient(w)
v = rho * v - learning_rate * dw
w += v2. SGD + Momentum
v = 0
for t in range(num_steps):
dw = compute_gradient(w)
v = rho * v + dw
w -= learning_rate * vSGD+Momentum이 서로 다른 방식으로 공식화된 것을 볼 수 있지만, 동일한 x 시퀀스를 제공한다.
Nesterov Momentum

- 왼쪽은 SGD+Momentum으로 현재 지점의 기울기를 속도와 결합하여 가중치를 업데이트한다.
- 오른쪽은 Nesterov Momentum으로 현재 위치에서 gradient를 계산하는 것이 아니라, 속도를 이용하여 업데이트될 때까지 기다린 후 "예견된" 위치에서 gradient를 계산하고 속도와 혼합하여 실제 업데이트 방향을 얻는다.
- Momentum방식의 경우 관성에 의해 훨씬 더 멀리 갈 수 있다는 단점이 있는 반면, NAG 방식의 경우 일단 Momentum으로 이동을 반 정도 한 후 어떤 방식으로 이동해야할 지를 결정한다. 따라서 Momentum 방식의 빠른 이동에 대한 이점은 누리면서도, 멈춰야 할 적절한 시점에서 제동을 거는 데에 훨씬 용이하다고 생각할 수 있을 것이다.
v = 0
for t in range(num_steps):
dw = compute_gradient(w)
old_v = v
v = rho * v - learning_rate * dw
w -= rho * old_v - (1 + rho) * vAdaGrad
- Adaptive Gradient
- 변수들을 update할 때 각각의 변수마다 step size를 다르게 설정해서 이동하는 방식
- 지금까지 많이 변화하지 않은 변수들은 step size를 크게 하고, 지금까지 많이 변화했던 변수들은 step size를 작게 한다.
grad_squared = 0
for t in range(num_steps):
dw = compute_gradient(w)
grad_squared += dw * dw
w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)- 문제 : 학습을 계속 진행하면 step size가 너무 줄어든다. G 에는 계속 제곱한 값을 넣어주기 때문에 G의 값들은 계속해서 증가하기 때문에, 학습이 오래 진행될 경우 step size가 너무 작아져서 결국 거의 움직이지 않게 된다. 이를 보완하여 고친 알고리즘이 RMSProp과 AdaDelta이다.
What happens with AdaGrad?
Progress along “steep” directions is damped;
progress along “flat” directions is accelerated
RMSProp
- Leak Adagrad
- AdaGrad의 gradient의 제곱값을 더해나가면서 구한 부분을 합이 아니라 지수 평균으로 바꾸어서 대체.
- 이럴 경우 AdaGrad처럼 가 무한정 커지지는 않으면서, 최근 변화량의 변수간 상대적은 크기 차이는 유지할 수 있다.
- RMSProp에서 step size는 점점 줄어들기에 SGD + Momentum에 비해 overshoot이 훨씬 덜 한 것을 볼 수 있다.
# AdaGrad
grad_squared = 0
for t in range(num_steps):
dw = compute_gradient(w)
grad_squared += dw * dw
w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)
# RMSProp
grad_squared = 0
for t in range(num_steps):
dw = compute_gradient(w)
grad_squared = decay_rate * grad_squared + (1 - decay_rate) * dw * dw
w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)Adam
- RMSProp + Momentum
- Momentum 방식과 유사하게 지금까지 계산해온 기울기의 지수평균을 저장하며, RMSProp과 유사하게 기울기의 제곱값의 지수평균을 저장한다.
moment1 = 0
moment2 = 0
for t in range(num_steps):
dw = compute_gradient(w)
moment1 = beta1 * moment1 + (1-beta1) * dw
moment2 = beta2 * moment2 + (1-beta2) * dw
w -= learning_rate * moment1 / (moment2.sqrt() + 1e-7)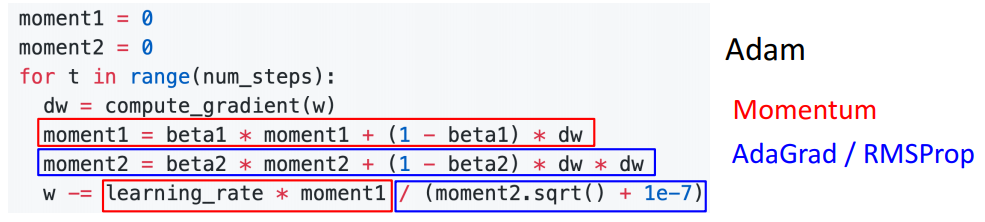

What happens at t=0? (Assume beta2 = 0.999)

참고 강의
https://www.youtube.com/watch?v=f3gMzIt_d-A&feature=youtu.be
참고 사이트
https://kmiiiaa.tistory.com/14?category=907348
https://github.com/aikorea/cs231n/blob/master/optimization-1.md
http://aikorea.org/cs231n/neural-networks-3/
https://kmiiiaa.tistory.com/14
https://fabj.tistory.com/49
내 기준에 이해하기 쉬웠던 블로그 1 🌟🌟
내 기준에 이해하기 쉬웠던 블로그 2 🌟🌟🌟