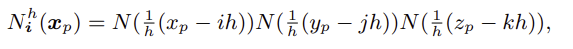Intro

개요

그래픽스 랩실 연구 주제를 눈과 상호작용하는 사람 동작의 생성을 하게 되었고, 그 시작으로 Disney의 '겨울왕국'에 사용된 눈 시뮬레이션 기술에 대한 논문을 읽고 분석하게 됨.

논문 제목 및 주제

제목: A material point method for snow simulation (Siggraph 2013)
주제: 실제와 같은 눈 시뮬레이션을 위한 구성 모델과 시뮬레이션 기술 제시

---

Abstract

눈이 가지는 특수성 때문에 기존의 고체,액체 기술은 눈에 대하여 설득력 있는 결과를 생성하는 것이 어려움. graphics community가 눈의 Accumulation, Rendering을 고민해 왔지만 아직 눈 역학 애니메이션은 완전히 해결되지 않음.

이 논문은 hybrid Eulerian/Lagrangian Material Point Method와 탄성-소성(elasto-plastic) 구성 model을 활용하는 새로운 눈 시뮬레이션 방법을 제시한다.

이 방법은 연속체 기반이며, 이 방법의 hybrid 특성은 regular Cartesian grid를 사용하여 자체 충돌 및 깨짐을 자동화 할 수 있게 한다. 또한, 이 방법은 Lagrangian particle의 수와 무관한 조절을 가지는 grid-based semi-implicit 통합 방식을 유도할 수 있다.

---

1. Introduction

보통 눈의 효과를 얻기 위해 사용되는 solver들은 종종 한 종류의 눈으로 처리된다. 그러므로, 한 가지 눈 solver에서 어려운 눈 동작을 처리하는 특수한 solver가 필요하다.
※ sovler: 시뮬레이션 소프트웨어 내부의 수식 계산을 담당하는 부분

눈은 계속해서 다양한 위상 효과를 가져서 때로는 고체로, 때로는 유체로 작동한다. 따라서 discrete coupling 대신, 한 영역에서 물질의 연속체를 동시에 처리해야 한다.

이 논문에서는 이를 위해 다음과 같은 두 가지 내용을 제시한다.

1) Develop a semi-implicit MPM

2) New snow constitutive model

---

2. Overview

이 논문에서는 엔지니어링 응용을 위해 고안된 이론과 모델을 기반으로 하여 현상학적 관찰을 기반으로 경험적 모델을 도출하는데 집중하였다.

2.1 MPM overview

• Material Point Method (MPM)은 복잡한 눈 화면에서 발생하는 광범위한 물질의 stiffness(강성), collsion(충돌), topological change(위상 변화)를 처리하기 위한 방법이다. [Sulsky et al.1995]

• MPM 방법은 Lagrangian 물질 입자를 Eulerian Cartesian grid와 결합한다. 이때, Lagrangian mesh 연결이 필요하지 않다.

• SPH과 같이 nondissipative Lagrangian 입자를 통해 질량을 추적함으로써 순수한 Eulerian 방법 보다 성능이 뛰어나다.

• PLC/FLIP solver와 마찬가지로 MPM은 background Eulerian grid를 사용하여 자체 충돌 및 깨짐을 처리한다. (동작중 많은 위상변화를 일일히 명시할 수 없으므로)

Lagrange vs Euler

---

Lagrange description : 입자 하나하나에 초점을 맞추어 각강의 입자를 따라가면서 그 입자의 물리량을 나타내는 방법

Euler description : 공간상에서 고정되어 있는 각 지점을 통과하는 물체의 물리량을 표현하는 방법

Lagrangian particle

---

Lagrangian particle는 입자가 유체의 요소인 것처럼 움직일 때의 입자를 말함. 이 입자 사이에는 연결이 없으므로 복잡성에 관계없이 자유롭게 이동하고 유체처럼 흘러가는 역학에 의해 움직인다.

Eulerian Cartesian grid

???

2.2 4가지 주요 속성에 대한 다양한 방식 비교

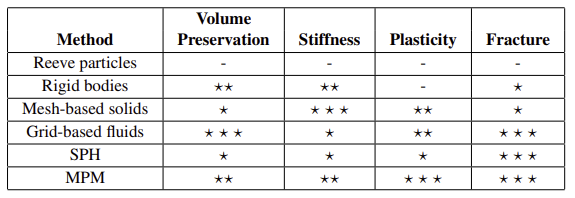
• 부피보존 : 눈은 액체와 달리 압축가능하지만 부피 보존이 중요하다.

• 단단함 : MPM은 deformation gradient가 덜 정확하기 때문에 mesh-based 탄성만큼 이를 수행할 수 없지만, deformation gradient가 분산되지 않고 위치와 동기화된 상태를 유지하므로 grid-based 탄성보다는 효과적이다.

• 가소성 : MPM은 grid-based fluid보다 angular momentum(각 운동량)을 전환하는 일을 잘한다. 또, mesh-based FEM 방법은 극단적인 변형이 있는 경우 다시 mesh가 필요하지만, MPM은 mesh 되지 않은 입자만 추적하면 된다.

• MPM은 가소성과 깨짐에 있어서 이점이 있지만 탄성 정확도는 그만큼 낮아진다.

※ 탄성 - 돌아가려는 성질, 소성 - 그대로 유지하려는 성질

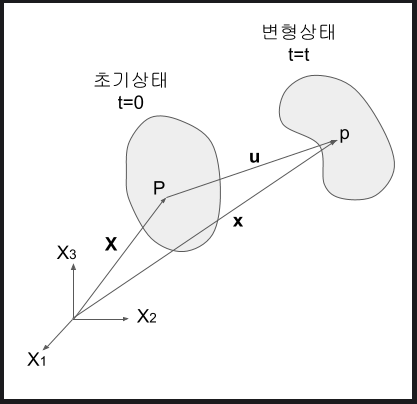
deformation gradient

---

X를 물체의 초기 위치, x를 물체의 변형 후 위치라고 할 때, x좌표는 mapping 함수 f에 의해서 x=f(t,X)로 표현 가능하다.

변형 후 위치가 초기 위치의 함수이기 때문에 미분이 가능하다. 이 여기서의 이 도함수 F를 deformation gradient라고 한다. (F = $\frac{∂x}{∂X}$)

이 F는 행렬로 표현 가능하고, 원래 위치 x에 이 F를 곱하면 변형된 위치 X가 나온다.

---

3. Material point method (MPM)

변형 전 위치 $X$와 변형 후 위치 $x$에 대하여 다음과 같은 mapping 함수를 구할 수 있고, deformation gradient F는 다음과 같다.

$x = φ(X)$, $F = \frac{∂φ}{∂X}$

또한, 이 mapping 함수 $φ(X)$는 질량 보존, 운동량 보존, 탄성-소성 구성 관계에 따라 변한다.

질량 보존 : $\frac{Dρ}{Dt} = 0$

운동량 보존 : $ρ · \frac{Dv}{Dt} = ∇ · σ + ρg$

탄성-소성 구성 관계 : $σ = \frac{1}{J} · \frac{∂Ψ}{∂F_E} · F_E^T$

---

σ - Cauchy stress(응력) : 물체 내부의 단위 면적당 힘
Ψ - 탄성-소성 potential energy 밀도
$F_E$ - $F$의 탄성 부분
$J = det(F)$

3.1 MPM

• MPM 방법의 기본 아이디어는 각 입자별로 질량, 운동량, deformation gradient를 추적하는 것이다. 이러한 많은 양의 입자에서 Lagrangian 연결 방법은 $\frac{Dρ}{Dt}$과 $ρ · \frac{Dv}{Dt}$의 이산화를 쉽게 해준다.

• 하지만, Lagrangian 입자들은 입자간 연결이 없으므로(거의없나? 아에 없나?) 응력 기간 힘 평가에 필요한 도함수 계산이 복잡해진다.
  => regular background Eulerian grid를 통해 이 문제를 해결.

• 이 regular background Eulerian grid에 대한 보간 함수는 weak form을 사용하여, 표준 FEM 방식으로 $∇ · σ$ 항을 이산화하는데 사용됨. [Steffen et al. 2008]에서 처럼 grid 기반 함수로 1차원 입방 B-spline 이항 곱을 사용한다.(??)

interpolation functions (보간 함수)

i = (i,j,k) : grid index
$x_p$ = ($x_p, y_p, z_p$) : evaluation position(평가 위치)
h : grid spacing (grid의 간격)

$w_{ip}$ = $N_i^h$ ($x_p$)

• 이러한 보간 함수들은 Eulerian grid의 node에서 힘을 계산하므로, grid node에서 속도를 update할 수 있도록 먼저 입자에서 grid로 질량과 운동량을 옮겨주어야 한다.

• update된 속도는 FLIP 또는 PIC 방식의 입자로 다시 back하여 옮겨진다.
  (이 과정은 위의 $w_{ip}$ 가중치를 사용하여 수행됨.)

• 각 grid의 값을 얻는 것은 그 grid의 위치 (i, j, k)에 대하여 주위 모든 particle을 고려하여 식에 대입하는 것이다(?.맞는지 모름, 고민 더 필요)

3.2 Full method(outline of full update procedure)

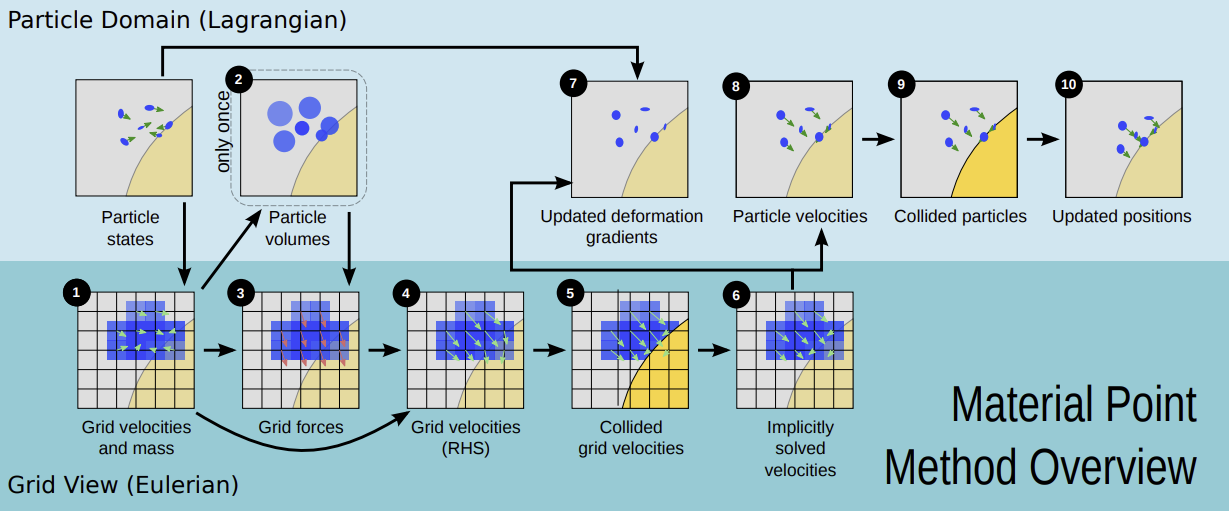
• <1> Rasterize particle data to the grid

  각 입자의 무게,속도를 grid로 전달.
  (속도는 운동량 보존을 위해 normalize된 가중치를 곱한다)

  $m_i^n$ = $∑_pm_pw^n_i$$_p$

  $v^n_i$ = $∑_pv^n_pm_pw^n_i$$_p$ / $m^n_i$

• <2> Compute particle volumes and densities

  • 첫번째 timestep에서만 한 번, 힘을 이산화하기 위해 입자 하나하나의 부피 개념이 필요함. (연속체 단위로 생각하기 때문에 한 입자의 부피를 구해 그 부피에 작용하는 것을 그 입자안의 모든 물질의 작용이라고 이산화하기 위함인가??)
  • 한 cell의 밀도를 $m^0_i / h^3$ 으로 구할 수 있는데, 이는 결국 1번에서 얻은 무게에 의해 다음과 같고, 그로인한 p의 부피도 다음과 같이 구할 수 있다.

    $ρ^0_p$ = $∑_pm_i^0w^0_i$$_p$ / $h^3$

    $V^0_p = m_p / ρ^0_p$

• <3> Compute grid forces

  방정식 1에 의해 각 grid의 힘을 구한다. 이때 xˆ$_i$ = x$_i$.

• <4> Update velocities on grid

  1번에서 구한 기존의 grid 속도v를 방정식 3을 사용하여 $v^*_i$로 update한다.

• <5> Grid-based body collisions

  $v^*_i$에 대해서 충돌을 고려한다. ( 충돌 과정은 뒤에 자세히 설명 )

• <6> get $v_i$n+1

  semi-implicit 적분을 위해 방정식 2에서 linear system을 품.
  explicit 시간 적분일 경우에는 간단히 $v_i$n+1 = $v^*_i$로 둠.

• <7> Update deformation gradient

  각 입자에 대해 deformation gradient를 update 한다.

  $F_p^{n+1}$ = ( I + ∆t ∇$v_p^{n+1}$) · $F_p^n$

  ---

  ∇$v_p^{n+1}$ = $∑_iv_i^{n+1}$ · (∇$w^n_{ip}$)$^T$

  ( 탄성-소성 부분의 deformation gradient F update에 대해서는 뒤에 자세히 설명)

• <8> Update particle velocities

  한 단계가 지난 n+1 에서의 입자 속도 $v_p^{n+1}$는 다음과 같다.

  $v_p^{n+1}$ = (1 - α) · $v_{PICp}^{n+1}$ + α · $v_{FLIPp}^{n+1}$

  ---

  $v_{PICp}^{n+1}$ = $∑_iv_i^{n+1}$ · $w^n_{ip}$

  $v_{FLIPp}^{n+1}$ = $v^n_p$ + $∑_i(v_i^{n+1} - v_i^n)$ · $w^n_{ip}$

  ※ 보통 α = 0.95

• <9> Particle-based body collisions

  $v^{n+1}_p$에 대해서 충돌을 고려한다. ( 충돌 과정은 뒤에 자세히 설명 )

• <10> Update particle positions

  최종적으로 다음의 식을 이용해 각 입자의 position을 update한다.

  $x^{n+1}_p = x^n_p + ∆tv^{n+1}_p$

---

4. Constitutive model

눈의 움직임은 눈이 물과 얼음의 성질 (고체&액체)을 동시에 가지고 있고, 이 각각의 성질이 움직임에 많은 영향을 끼치기 때문에 복잡하다. 이러한 눈의 움직임은 많은 외부 환경에 의해 드라마틱하게 바뀐다. (온도,습기,밀도,눈 나이 등)

이 논문에서는 [Meschke et al. 1996]의 방법을 사용하여 눈 구성 모델을 구성하였다. 여기에서 일반적인 그래픽스 모델과 결합된 초탄성에 대한 유한 변형률 곱셈 소성(??)의 단순화된 처리가 시각적 사실을 표현하기에 충분하다는 것을 얻음.

이 접근 방식은 경화 행동의 단순화와 소성 산출 기준을 정의할 때, 주 stress(응력)보다 주 stretch를 사용한다. 이때 경화 행동의 초탄성 에너지 밀도에서 Lame 매개변수의 수정만 필요로 한다. (stress-based 소성은 물리적 정확도가 높고, stretch-based 소성은 user가 시뮬레이션의 시각적 동작의 이점이 있다.)

multiplicative plasticity 이론에서는 흔히, deformation gradient F를 탄성 부분($F_E$)과 소성 부분($F_P$)로 나눈다. ($F = F_EF_P$)

구성모델은 탄성-소성 에너지밀도 함수의 관점에서 다음과 같이 정의 된다.

$Ψ(F_E,F_P) = µ(F_P)||F_E - R_E||^2_F$ + $\frac{λ(F_P)}{2}·(J_E -1)^2$

---

$µ(F_P) = µ_0 e^{ξ(1-J_P)}$

$λ(F_P) = λ_0 e^{ξ(1-J_P)}$

$J_E$ = det $F_E$ , $J_P$ = det $F_P$

$F_E = R_ES_E$

$λ_0, µ_0$ : 초기 Lame 계수 ($F_P$의 함수)

ξ = 무차원 소성 경화 매개변수

deformation gradient의 특이값들을 사용하여, 탄성과 소성인 변형 부분을 정의한다.
임계 응압 $θ_c$와 stretch $θ_s$를 소성 변형(부서짐)을 시작하는 임계값으로 정의함.
=> $F_E$를 [1 - $θ_c$, 1 + $θ_s$]의 범위로 제한한다.

변형이 임계 임계값을 초과하면 소성 변형이 시작된다. 이 변형은 $µ(F_P), λ(F_P)$에 영향을 미쳐서, 압축시 더 강하고, 신축시 약해져서 사실적인 눈 현상을 얻을 수 있게 한다.

• $θ_c$와 $θ_s$은 재료가 부서지기 시작하는 시점을 결정한다.
  $θ_c$와 $θ_s$가 작을수록 건조하고 가루같은 눈, 클수록 젖고 덩어리진 눈

• 경화계수 ξ는 물질이 소성이 되면 얼마나 빨리 부서지는지 결정한다.
  ξ가 클수록 얼음눈(취성), 작을수록 진흙눈(연성).

---

5. Main Logic

5.1. Stress-based forces and linearization

총 탄성 위치 에너지는 에너지 밀도 Ψ로 표현될 수 있다.
stress-based 힘의 MPM 공간 이산화는 Eulerian grid node 물질 위치에서 탄성 에너지의 이산 근사치를 미분하는 것과 같다. 이때, 실제로 Eulerian grid를 변경하지 않으므로, grid 위치의 변화는 grid node 속도에 의해 결정된다.

$xˆ_i = x_i + ∆tv_i$

$Φ(xˆ) = \displaystyle\sum_{p} V^0_p·Ψ(Fˆ_{Ep}(xˆ) , F^n_{Pp})$

$Fˆ_{Ep}(xˆ) = (I + \displaystyle\sum_{i}(xˆ_i - x_i)(∇w^n_{ip})^T)·F^n_{Ep}$

[Sulsky et al. 1995]에 따름

---

$x_i$ : grid node i의 position
$xˆ_i$ : 변경된 grid의 position
xˆ: 모든 grid node $xˆ_i$의 vector
$Φ(xˆ)$ : 총 탄성 potential에 대한 MPM 근사값
$V^0_p$ : 처음에 입자 p에 의해 차지되었던 물질의 부피
$F^n_{Pp}$ : 시간 $t^n$에서 입자 p의 F의 소성 부분
$Fˆ_{Ep}$ : xˆ의 탄성 부분

stress-based MPM 공간 이산화는 $Φ(xˆ)$을 xˆ으로 미분한 것과 같고 이는 다음과 같다.
$f_i(xˆ)$ : grid node i에서 탄성 응력에 의한 힘

$-f_i(xˆ) = \frac{∂Φ}{∂xˆ_i}(xˆ) = \displaystyle\sum_{p} V^0_p · \frac{∂Ψ}{∂F_E}(Fˆ_{Ep}(xˆ),F^n_{Pp}) · (F^n_{Ep})^T · ∇w^n_ip$

방정식1

$f_i(xˆ) = -\displaystyle\sum_{p}V^n_p · σ_p · ∇w^n_ip$

---

$σ_p$ : Cauchy stress
$σ_p = \frac{1}{J^n_p}·\frac{∂Ψ}{∂F_E}·(Fˆ_{Ep}(xˆ),F^n_{Pp})·(F^n_{Ep})^T$
$V^n_p = J^n_pV^0_p$ : 시간 $t^n$에서 입자 p의 부피

xˆ에 대한 potential의 Hessian 행렬을 사용하여 update의 탄성부분에 대한 암시적 단계를 수행할 수 있음. (??)

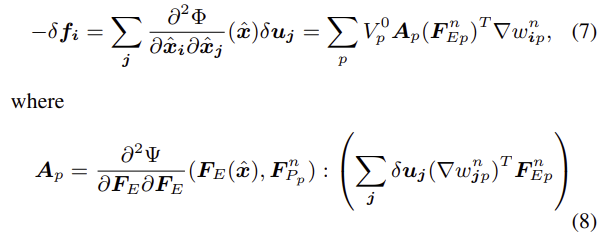
Semi-implicit update

방정식2

$\displaystyle\sum_{j} (Iδ_{ij} + β∆t^2m^{-1}_i \frac{∂^2Φ^n}{∂xˆ_i∂xˆ_j})·v_j^{n+1} = v^*_i$

방정식3

$v^*_i = v^n_i + ∆tm^{-1}_i f^n_i$

※ β는 다음 중에서 고름 { explicit: 0 , trapezoidal: 1/2 , backward Euler: 1 }

---

5.2. Deformation gradient update

$Fˆ_{Ep}^{n+1} = ( I + ∆t ∇v_p^{n+1}) · F_{Ep}^n$ 이고,

$Fˆ_{Ep}^{n+1} = F^n_{Pp}$ 이여서 초기의 모든 변화는 변화구배의 탄성 부분에만 기여한다.

즉, $F^{n+1}_p = (I + ∆t ∇v_p^{n+1}) · F_{Ep}^n · F_{Pp}^n = Fˆ^{n+1}_{Ep}·Fˆ^{n+1}_{Pp}$

그다음, 임계 변형값을 초과하는 $Fˆ^{n+1}_{Ep}$의 부분을 찾아서 이것들을 $Fˆ^{n+1}_{Pp}$에 넣는다.

다음 특이값 분해(?)를 계산
$Fˆ^{n+1}_{Ep} = U_p \displaystyle\sum^{ˆ}$$_p V_p^T$

이 특이값을 허용된 범위로 고정
$∑_p$ = clamp($\displaystyle\sum^{ˆ}$ $_p, [1- θ_c,1+θ_s])$

∴ $F^{n+1}_{Ep} = U_p ∑_p V_p^T$

∴ $F^{n+1}_{Pp} = V_p ∑_p^{-1} U_p^T F^{n+1}_p$

※ $F^{n+1}_p= F^{n+1}_{Ep} · F^{n+1}_{Pp}$를 만족함

특이값 분해?

---

5.3. Body Collisions

• 각 time step마다 충돌 body에 대한 충돌을 두 번 처리한다.

  1) 힘이 grid 속도에 적용된 직후 grid 속도 $v^*_i$에 처리
  semi-implicit integration의 case에서, 이 처리는 linear system의 right hand side에 기여하고, 충돌하는 grid node에 해당하는 자유도는 solve 중에 투영된다.
  2) 입자 속도 $v^{n+1}_p$에 위치를 update하기 직전에 한 번 더 충돌을 적용.
  보간으로 인한 입자 속도와 grid 속도 간의 사소한 불일치를 해결하기 위함.

• 두 충돌에서 충돌 processing은 같은 방식으로 이루어지며, 충돌은 비탄성이다.

• 물체는 level set으로 표현되어 충돌 탐지를 쉽게 만듦 ( 충돌 탐지: (φ ≤ 0)).

• 각 충돌마다 local 법선 $n(n = ∇φ)$과 물체 속도 $v_{co}$가 계산됨.

• 입자/grid 속도 $v$는 충돌 물체의 reference frame으로 전환됨.
  이때, $v_n = v_{ref}·n >= 0$ 이면 body가 분리된다는 뜻이고, 충돌이 적용되지 않음.

• ||$v_t$|| <= -$µv_n$ 이면 sticking impulse가 필요하고, $v'_{ref} = 0$으로 둔다.
  만약 아니면, 동적 마찰을 적용해야 한다. $v'_{ref} = v_t + \frac{µv_nv_t}{ ||v_t||}$
  • $v_t = v_{ref} - nv_n$: 상대 속도의 접선 부분
  • µ : 마찰 계수
  • ※ 여기서 '은 충돌이 적용되었음을 나타냄

• 마지막으로 충돌한 상대 속도를 reference frame에서 다시 world 좌표로 돌린다.

  $v' = v'_{ref} + v_{co}$

• 이 논문에서 충돌은 크게 두 종류

  • 1) 강체(rigid): 고정 level set과 잠제적으로 시간에 따라 변하는 강체 변환을 저장. 이 변환은 어느 point에서나 $φ, n, v_{co}$를 계산할 수 있게함.

  • 2) 변형(deforming): level set key frames을 load하고, 보간한다.
    $φ(x, t +γ∆t) = (1−γ)φ(x−γ∆tv_{co}, t)+γφ(x+(1−γ)∆tv_{co}, t+∆t)$
    ∵ $v_{co} = (1−γ)v(x, t)+γv(x, t+∆t)$

• 끈적한 충돌(sticky collision): 눈이 수직 또는 아래로 매달려 있는 표면에 달라붙는 현상을 위해 사용. 이 경우 정상 상대 속도가 0(수직) 또는 양수(중력으로 인한 under-hanging,분리)이기 때문에 Coulomb 마찰은 적절하지 않음.
  이러한 표면에 대한 충돌은 $v'_{rel}=0$으로 하여 매달려 표면에 달라붙는 효과를 보인다.

---

5.4 Rendering

discrete Cartesian grid는 물질 point의 상대적인 밀도를 측정하여 느슨한 눈과 꽉 채워진 눈 사이의 시각적 변화를 보여주는 방법을 제공하였다. 이를 통해 purely point-based 방법에 비해 rendering 이점을 제공.

얼음 결정의 Mie 산란 이론을 근사하는 Henyey Greaanstein 위상 함수를 사용, 부피 산란 방정식을 풀기 위해 체적(volumetric) 경로 추적기를 사용.

일반적으로 전방 산란, 소멸 계수 σt, 산란 albedo σs/σt를 얻기 위해 mean-cosine을 사용.
(σs : 산란 계수)

---

6. Experiments