MPM Method (Rasterize particle data to the grid)

남하욱·2022년 8월 22일

Snow Simulation

목록 보기

2/4

summury

MPM snow simulation의 첫 번째 단계인 Rasterize particle data to the grid를 수행하기 위한 개념과, 코드 내용 설명

개념

MPM 방법은 질량, 운동량, 변형구배를 추적하기 위해 particle을 사용한다.
이때, 각 particle은 position, 속도, 질량, 변형구배를 가지고 있음.
이러한 많은 양의 입자에서 Lagrangian 연결 방법은 Dρ/Dt와 ρ⋅Dv/Dt의 이산화를 쉽게 해준다. (질량 보존 법칙과, 운동량 보존 법칙을 위한 값들)
하지만, Lagrangian 입자들은 입자간 연결이 없으므로 응력 기반 힘 평가에 필요한 도함수 계산이 복잡해진다.
=> regular background Eulerian grid를 통해 이 문제를 해결
이 regular background Eulerian grid에 대한 보간 함수( $w_{ip}$ )는 weak form을 사용하여, 표준 FEM 방식으로 ∇⋅σ 항을 이산화하는데 사용됨. [Steffen et al. 2008]에서 처럼 grid 기반 함수로 1차원 cubic B-spline 이항 곱을 사용한다
각 node의 값을 얻는 것은 각 particle이 포함된 모든 node의 위치 (i, j, k)에 대하여 그 particle의 값과 $w_{ip}$ 을 사용하여 값을 구하고 그 모든 값을 node값에 더하는 것이다.
MPM의 시작단계에서 입자는 질량과 운동량을 grid node로 전환한다.
그리드 해석 후, 속도는 advection 단계를 수행하기 위해 입자로 다시 전송.
이 두 과정은 모두 보간 함수가 필요함.
※ advection(이류) : 공기나 해수 등에 의해 수증기, 염분 등의 물질이나 압력, 온도, 밀도, 운동량 등 유체가 가진 물리량이 운반되는 과정.

In Code

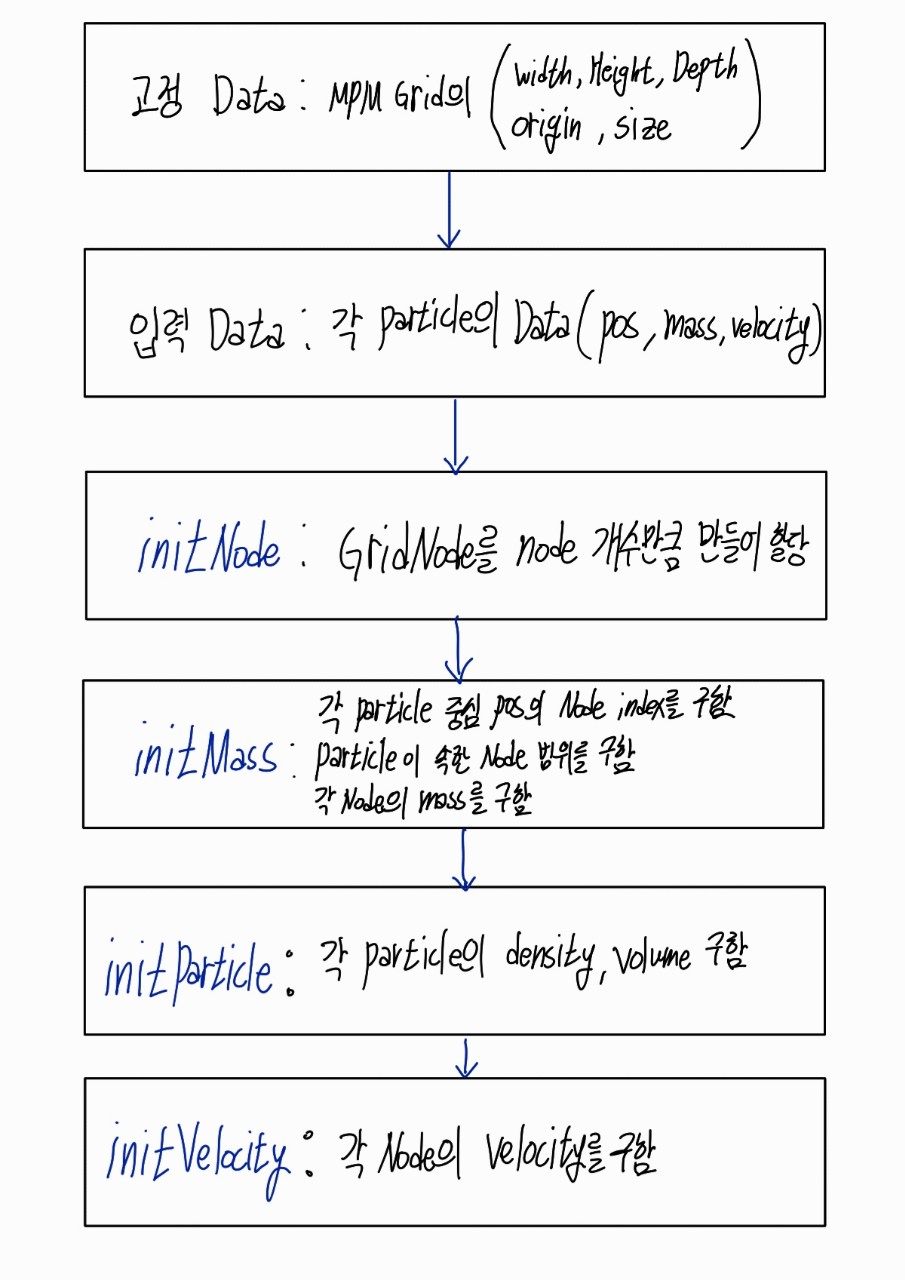
1. MPM Grid를 만듦 (in render.py)

mainGrid를 전역변수로 생성
이때, origin, size, gridWidth, gridHeight, gridDepth 값을 인자로 넣음.

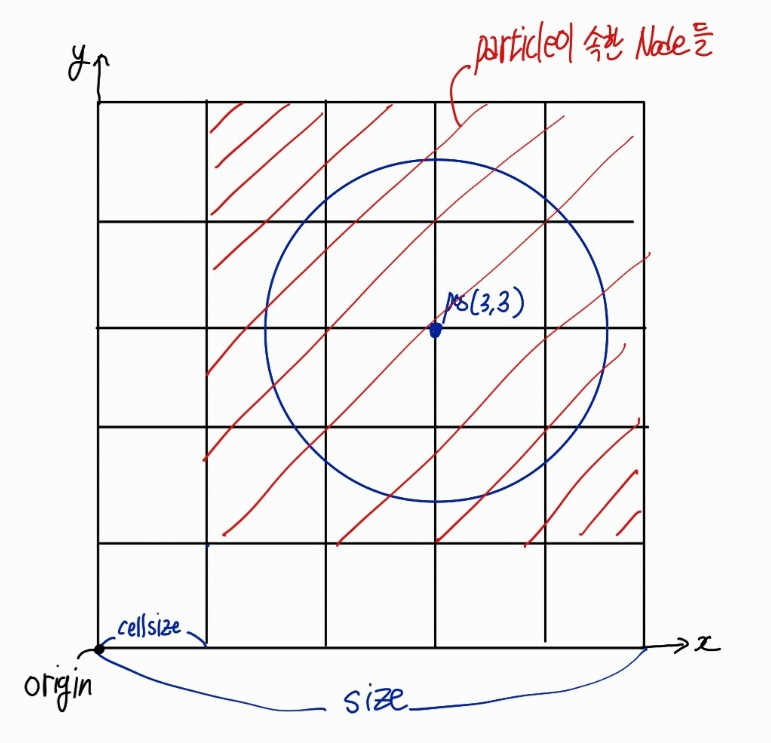
origin: grid의 시작지점

size : grid의 좌표상 (x,y,z) 크기

gridWidth, gridHeight, gridDepth : grid의 각 방향별 node의 개수

cellsize : grid의 각 방향별 한 node cell의 좌표상 길이 ( size를 각 gridW,H,D로 나눠서 구함, 논문에서 h에 해당)

invCellsize : 1/cellsize (논문에서 1/h에 해당, 자주쓰이는데 그때마다 계산하는 것 보다 미리 계산해놓으려는 의미)

bound : grid의 좌표상 x,y,z 시작과 끝을 나타내는 6개의 수

2. initGrid()를 통해 각종 init함수 호출(in render.py)

ParticleArray : particle객체들이 저장된 배열 (일단은 예시로 임의로 설정한 값을 가지는 paticle을 만들어 넣어줌)

2.1. initNode : 입력받은 gridW,H,D를 이용하여 좌표상의 값을 가지는 GridNode객체를 만들어 mainGrid의 nodes배열에 넣음. (nodeCount만큼의 GridNode 객체가 nodes배열에 넣어짐)

2.2. initParticle : 만든 ParticleArray를 인자로 넣어 mainGrid의 particles에 넣어줌. initMass()를 호출. 그 후, 각 particle들의 density와 volume을 계산하여 저장. 이때, volume의 반지름은 2에 근사됨.

2.3. initMass :

gridPos: 그 particle이 위치한 node의 index, 각 particle의 좌표상 위치 pPos와 grid의 시작 위치 origin과의 차이를 cellsize로 나눈 값.
(gridPos - 2 & gridPos +3)를 통해 particle이 속한 node의 시작,끝 index를 구함. (+3인 이유는 index에 그대로 값을 쓰면 포함되지 않는 범위가 되므로, 미리 +1을 더 하여 계산해 놓은 것, 실제로는 +2까지의 범위가 실제 bound)
이 particle이 속한 node를 모두 돌며, 이 particle의 질량에 가중치( $w_{ip}$ )를 곱한값을 모두 더하여 각 node의 질량을 구함.