
개념
타잔 알고리즘은 깊이 우선 탐색 알고리즘(DFS)을 활용해 SCC를 찾는 알고리즘입니다.
알고리즘 순서
- 방문하지 않은 정점에 대해 방문 순서에 따라 각 정점에 고유한 id를 매기고,
d[i] = ++id // 정점에 고유 id 할당- 정점을 스택에 삽입합니다.
stack.add(i) // 스택에 자신을 삽입- 이후 해당 정점과 연결된 모든 정점을 비교해 부모 정점을 찾고
var parent = d[i]
for (next in graph[i]) {
// 아직 방문하지 않은 정점이면, 탐색을 진행하고 부모 갱신
if (d[next] == 0) parent = min(parent, dfs(next))
// 방문은 했으나 SCC로 성립되지 않은 점이라면
else if (!finished[next]) parent = min(parent, d[next])
}- 그 정점이 자신이면 스택에서 자기 자신을 찾을 때까지 빼 SCC를 구해줍니다
// 자신과 자식 정점들이 갈 수 있는 가장 높은 정점이 자신일 경우. 즉 부모노드가 자기 자신인 경우
if (parent == d[i]) {
val scc = ArrayDeque<Int>()
// 스택에서 자기 자신을 찾을 때까지 SCC에 추가
while (true) {
val t = stack.removeLast()
scc.add(t)
finished[t] = true
if (t == i) break
}
sccList.add(scc)
}예시
아래의 예시를 통해 자세히 알아보겠습니다.
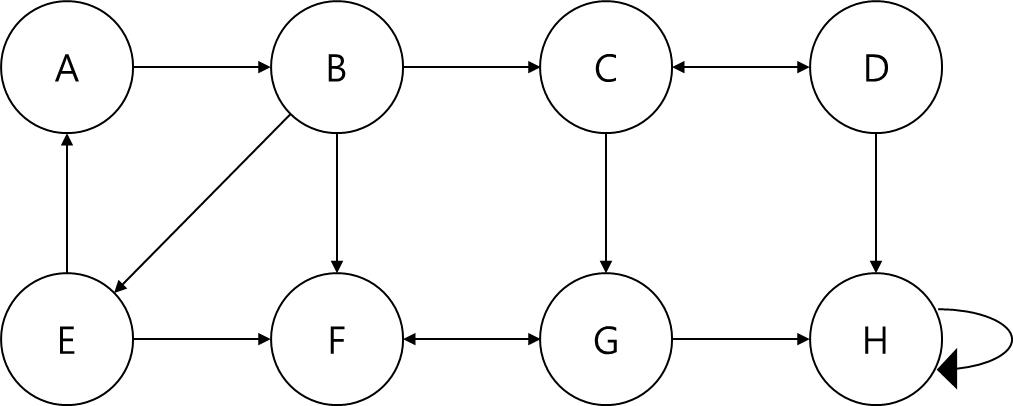
정점 A부터 탐색을 진행하겠습니다.
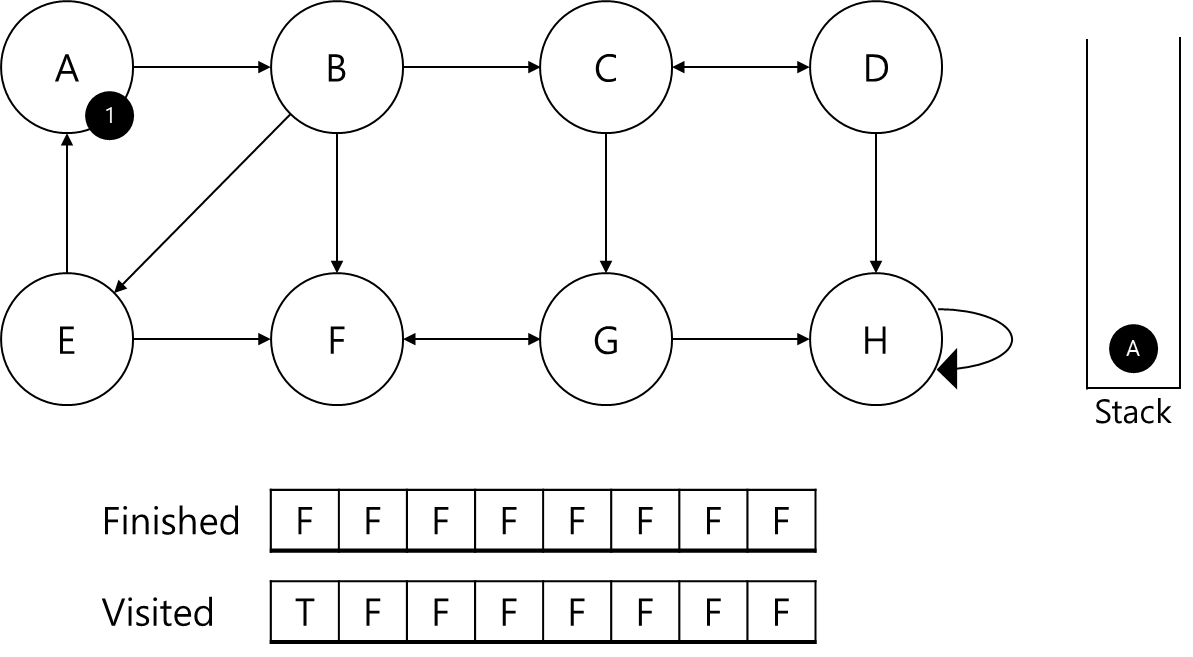
(finished 배열은 SCC 판별이 끝났는지, visited 배열은 해당 정점을 방문했는지를 저장하는 배열입니다.)
첫 번째로 방문했기 때문에 A에 1번 id를 부여하고 스택에 삽입해주겠습니다.
A와 연결된 B가 탐색이 되지 않아 A가 부모 노드인지 판별할 수 없네요.
B를 탐색해주겠습니다.

B에 2번 id를 부여하고, 스택에 추가해주겠습니다.
마찬가지로 B와 연결된 C, E, F에 대한 정보가 없어 B가 부모 정점인지 판별할 수 없네요.
C를 탐색해주겠습니다.

마찬가지로 C에 3번 id를 부여해주고, 스택에 추가해주었습니다.
C와 연결된 D와 G에 대한 정보가 없어 D를 탐색해주겠습니다.

D에 4번 id를 부여해주고 스택에 추가해주었습니다.
D와 연결된 H의 정보가 없으니 H를 탐색해주겠습니다.

H에 id 5번을 부여하고 스택에 추가해주었습니다.
H의 경우 부모 정점이 본인이다 보니 스택에서 본인이 나올 때까지 빼서 SCC 저장 배열에 저장하고 SCC 판별 배열인 finished 배열을 갱신해주겠습니다.
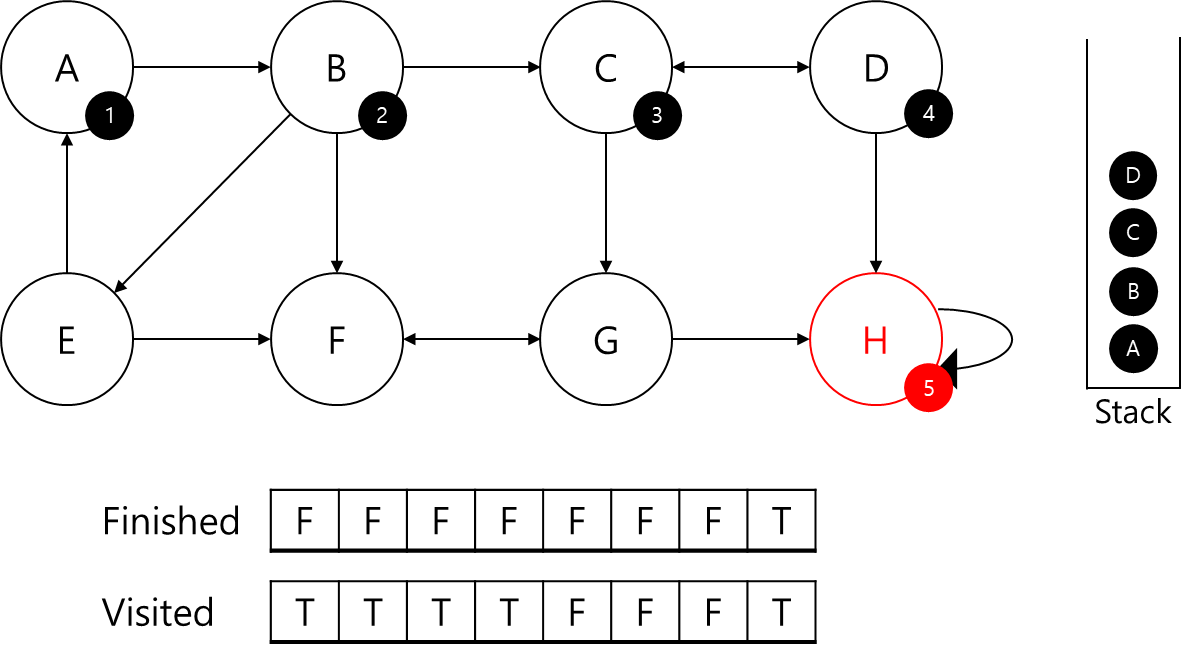
이제 부모 정점인 D로 이동하겠습니다.
D의 경우 연결된 C와 H의 부모 정점이 본인이 아니기 때문에, (4 != min(3, 5)) 본인의 부모인 C를 반환해주고 정점 C로 이동하겠습니다.
C에서는 D의 정보가 있지만 G의 정보가 없습니다. 따라서 G를 방문해서 C가 부모 정점인지 아닌지 알아보겠습니다.
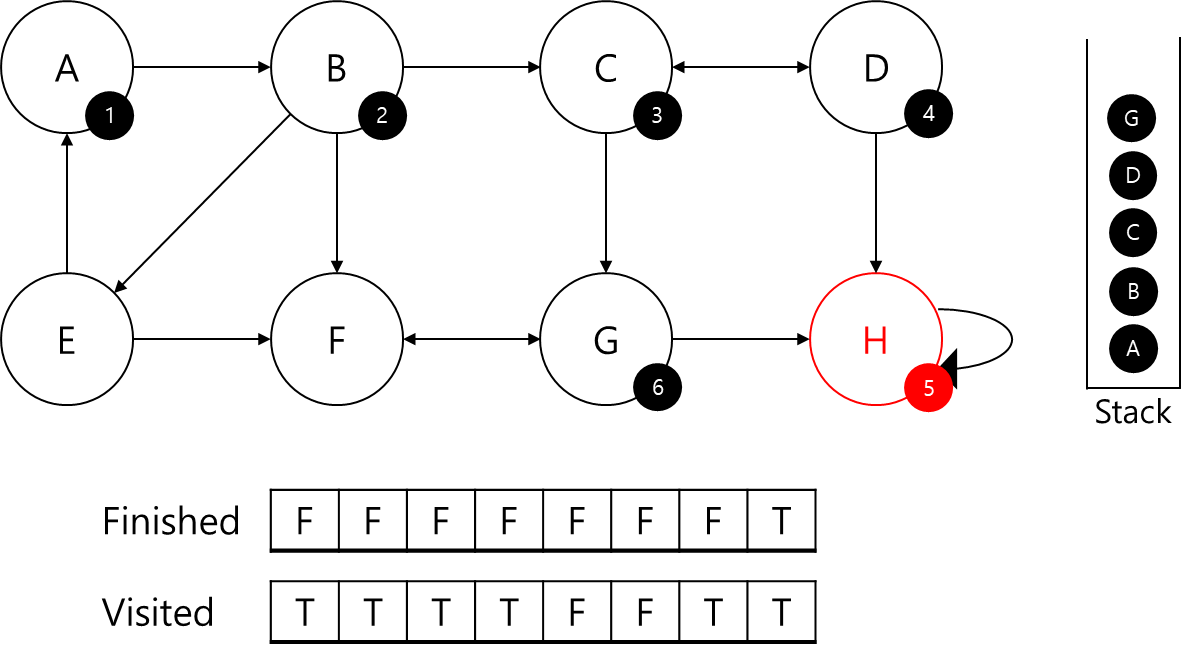
G에 ID 6을 부여해주고, 스택에 G를 넣어줍니다.
G는 F에 대한 정보가 없으므로 F를 탐색해줍니다.
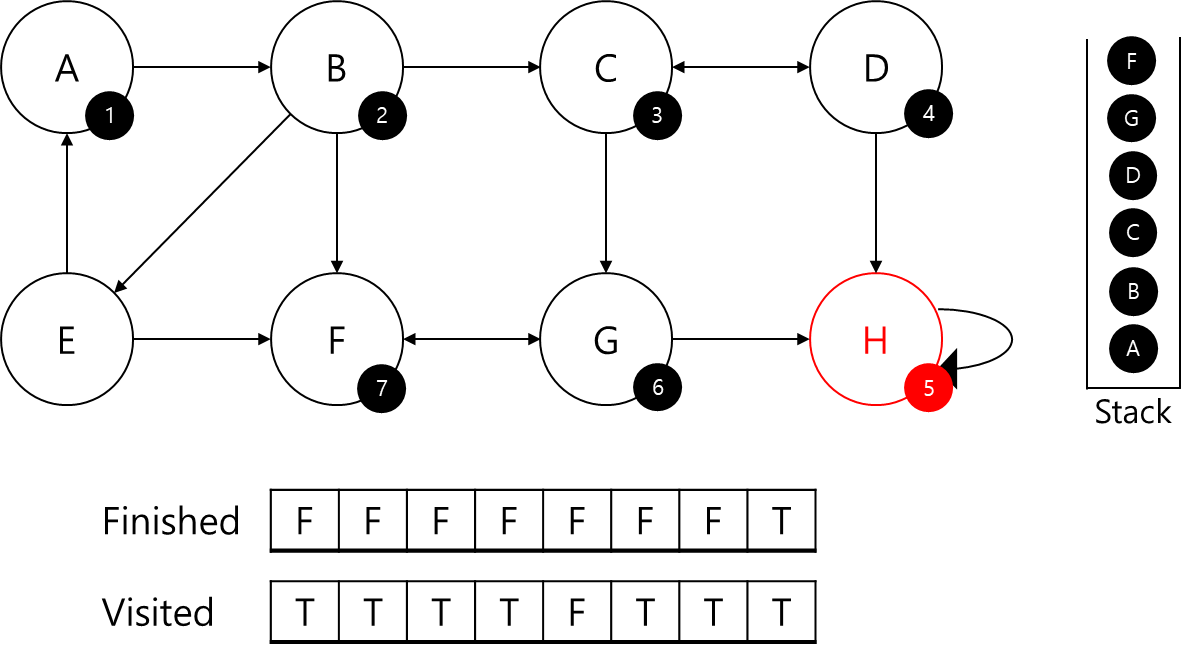
F에 7번 ID를 부여해주고 스택에 추가해줬습니다.
F의 경우 본인과 연결된 G에 대한 정보가 있는데, 본인의 부모이기 때문에 본인의 부모 정점인 F를 반환하고 G로 다시 이동하겠습니다.
이제 G에서는 F와 H의 정보가 있다 보니 본인이 부모 정점인지 아닌지 알 수 있습니다.
F의 부모는 본인이고, H는 이미 SCC이기 때문에 G는 부모 정점입니다.
Stack에서 본인이 나올 때까지 빼서 SCC에 추가하고 finished 배열을 갱신해주겠습니다.
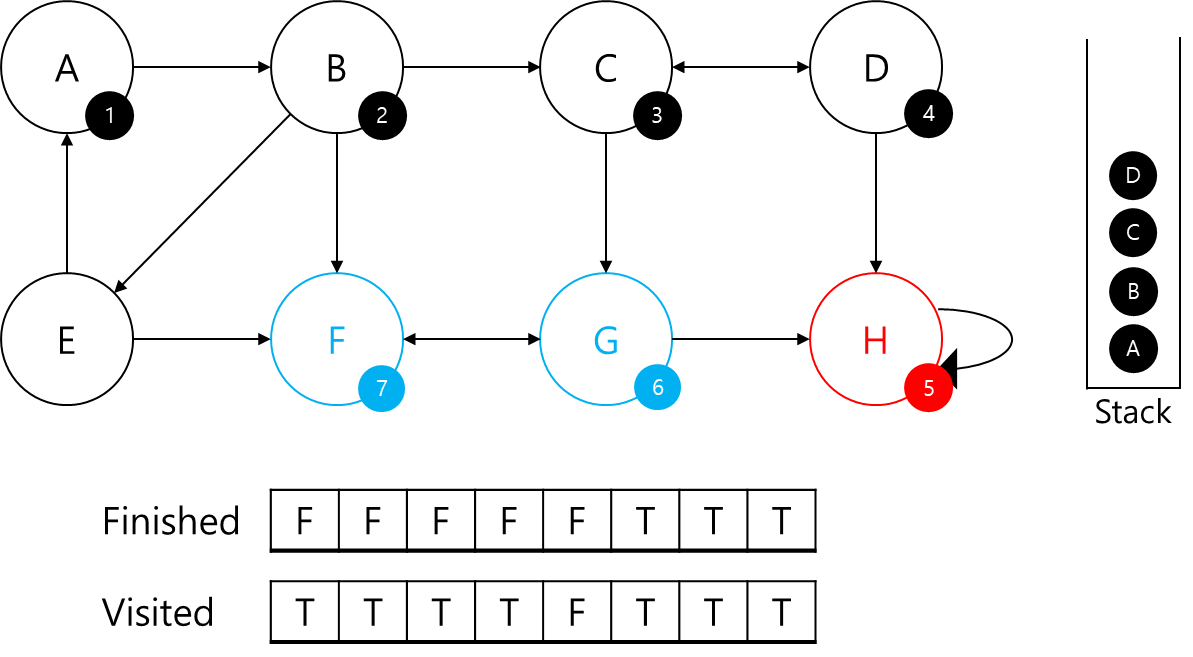
이제 C로 돌아가 보겠습니다.
C의 경우 D의 부모임을 알고, G는 이미 SCC로 판별났기 때문에 C는 부모 정점입니다.
따라서 C가 나올 때까지 Stack에서 빼서 SCC에 추가하고 finished 배열을 갱신해주겠습니다.
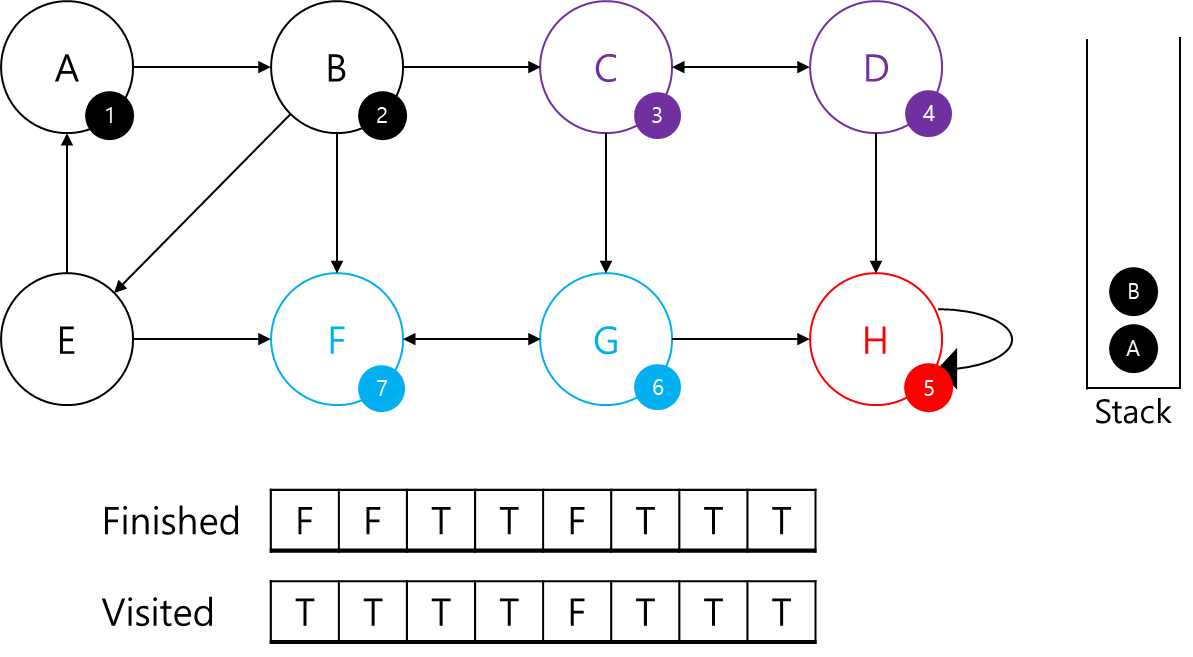
자 이제 B를 보겠습니다.
B의 경우 C를 탐색했으나, E와 F를 탐색하지 못했습니다.
E를 탐색해주겠습니다.
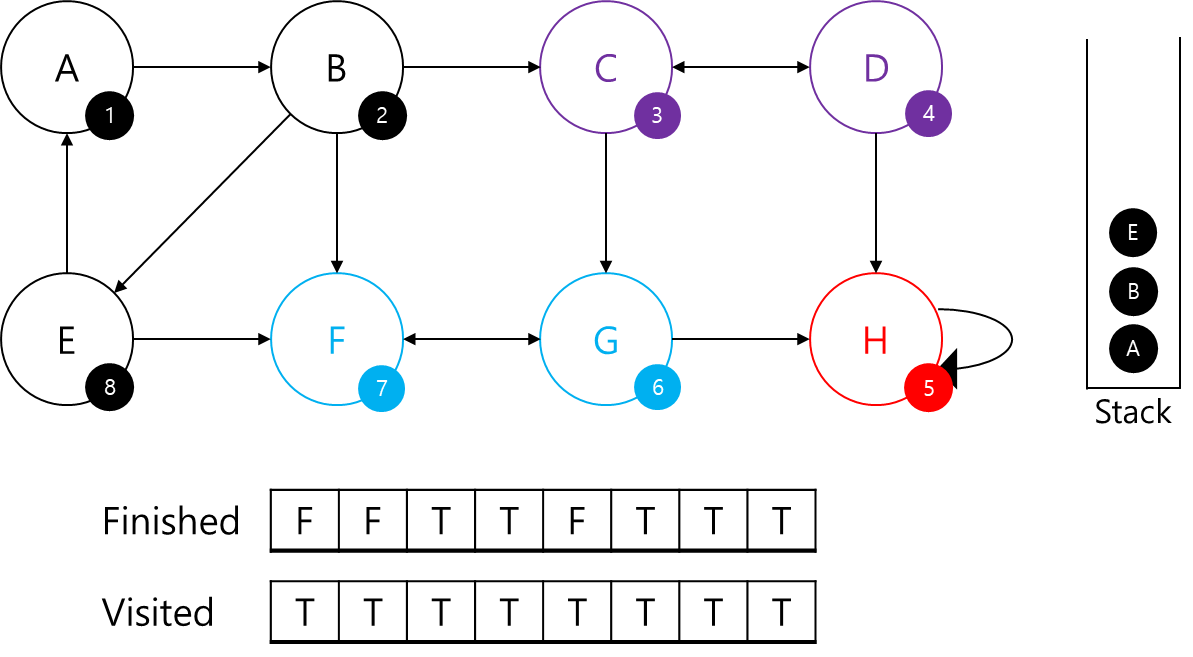
E에 8번 id를 부여해주고, 스택에 추가해주었습니다.
이제 E에 대해 탐색을 해보겠습니다.
E와 연결된 A는 E보다 먼저 방문했고, F는 SCC임이 판별났기 때문에 정점 E는 본인이 부모 정점이 아닙니다.
따라서 본인의 부모 정점인 A를 반환합니다.
이제 B에서 본인이 부모 정점임을 확인해봅니다.
C와 F는 SCC고, E에서 반환받은 부모 정점은 본인이 아니기 때문에 본인의 부모 정점인 A를 반환합니다.
A와 연결된 B에서 본인이 부모 정점임을 알게 되었네요.
stack에서 본인이 나올 때까지 빼서 SCC에 추가하고 finished 배열을 갱신해주겠습니다.
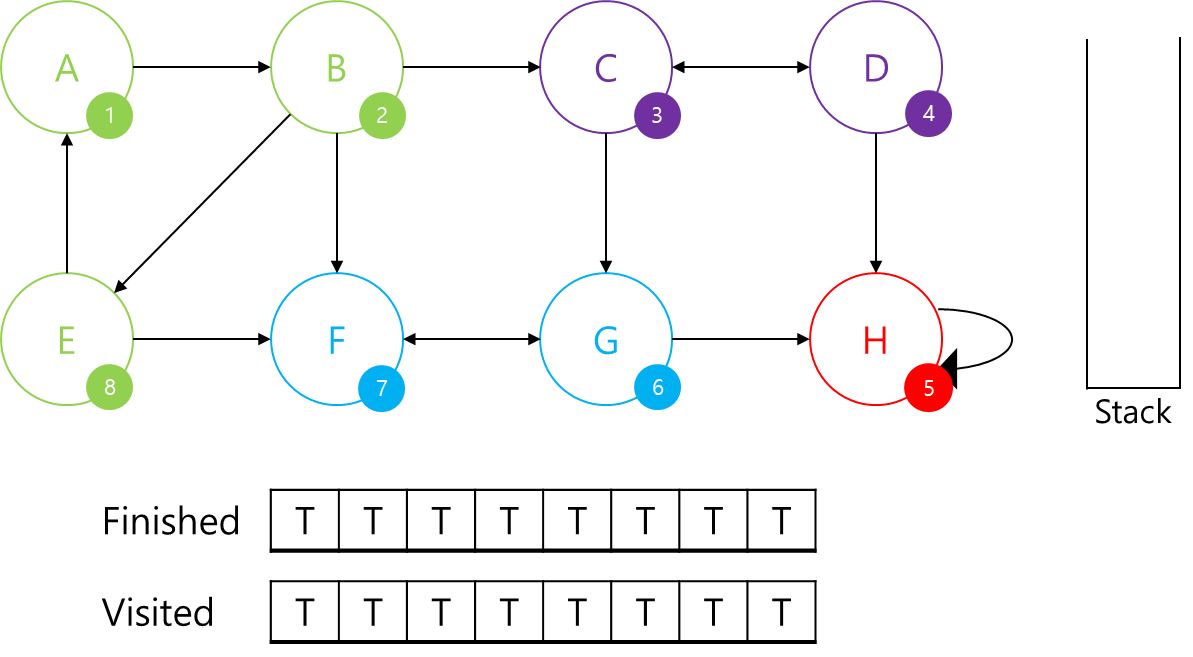
이렇게 모든 그래프를 탐색하고 SCC를 찾아보았습니다.
마치며
타잔 알고리즘은 코사라주 알고리즘과 같은 O(V + E)의 시간 복잡도를 가졌습니다.
타잔 알고리즘은 코사라주 알고리즘에 비해 구현이 어렵다는 단점이 있으나, DFS 1번으로 SCC를 구할 수 있다는 장점이 있습니다. (코사라주 알고리즘은 2번)
감사합니다.
참고
