[알고리즘] DFS(깊이 우선 탐색)-재귀, 스택(Stack)

DFS란?

대표적인 그래프 탐색 알고리즘이다. DFS는 깊이 우선 탐색(Depth First Search)이라는 알고리즘이며, 정점의 자식을 먼저 탐색하는 방식이다.

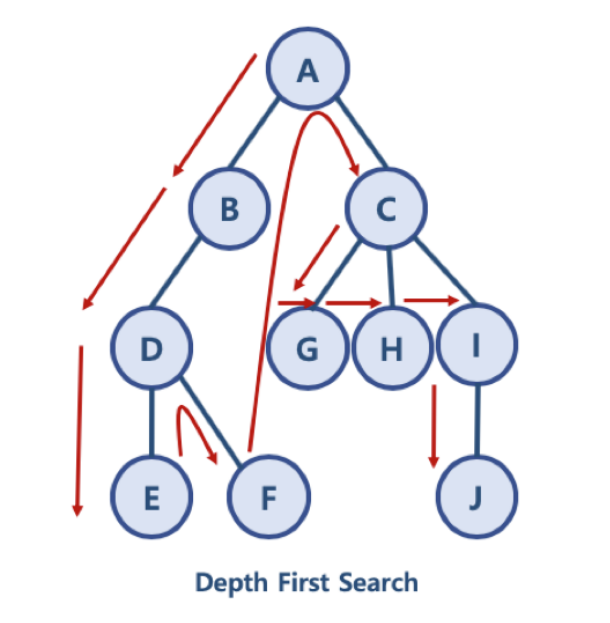
위의 그래프를 DFS 방식으로 순회하면 A - B -D - E - F - C - G - H - I - J 순으로 돌게 된다.

그래프(Graph)란?

그래프(Graph)란 요소들이 서로 복잡하게 연결되어 있는 관계를 표현하는 자료구조이다. 그래프는 정점(vertex)과 간선(edge)들의 집합으로 구성된다.

1. 인접 행렬을 이용한 그래프 구현

그래프의 정점을 2차원 배열로 만든 것이다. 정점의 개수가 N개라면 N*N 형태의 2차원 배열로 나태낸다. 행과 열은 정점을 의미하고 각 원소들은 정점 간의 간선의 유무(또는 가중치)를 나타낸다.

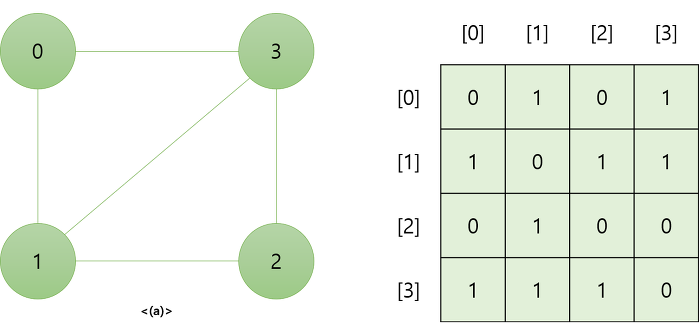
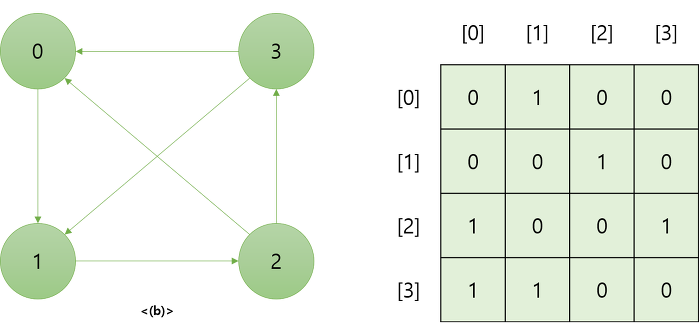
• 단점
  • 간선의 수와 무관하게 항상 N^2 크기의 2차원 배열이 필요하므로 메모리 공간이 낭비된다.
  • 인접 행렬 전체를 확인할 때 O(n²)의 시간이 소요된다.

2. 인접 리스트를 이용한 그래프 구현

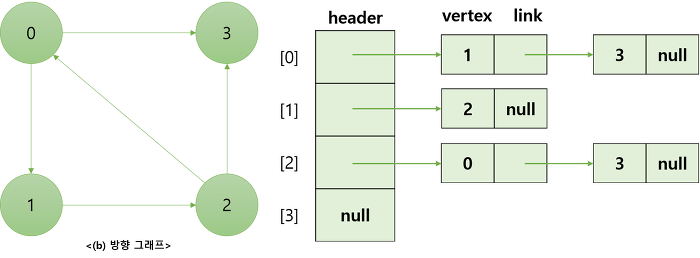
그래프의 각 정점에 인접한 정점들을 연결리스트(Linked List)로 표현하는 방법이다. 즉 정점의 개수만큼 인접 리스트가 존재하며, 각각의 인접 리스트에는 인접한 정점 정보가 저장되는 것이다. 그래프는 각 인접 리스트에 대한 헤드포인터를 배열로 갖는다.

무방향 그래프의 경우 간선이 추가되면 각각의 정점의 인접 리스트에 반대편 정점의 노드를 추가해야 한다.

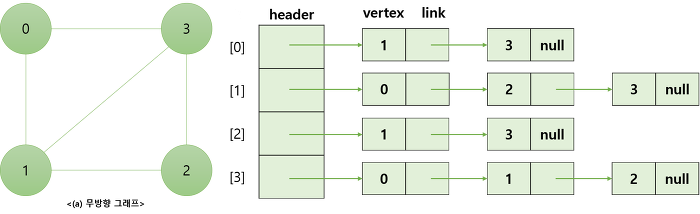
• 장점
  • 존재하는 간선만 관리하면 되므로 메모리 사용 측면에서 인접 행렬보다 효율적이다.
  • 모든 인접 리스트를 탐색할 때 O(n+e)의 시간이 소요된다.
• 단점
  • 두 정점을 연결하는 간선을 조회하거나 정점의 차수를 알기 위해서는 정점의 인접 리스트를 탐색해야 하므로 정점의 차수만큼의 시간이 필요하다. O(degree(v))
  • 구현이 비교적 어렵다.

이미지 출처 : https://kingpodo.tistory.com/46

💡DFS의 구현

1. 재귀 함수로 구현

# 0,0 -> 3,3까지 가는 길이 존재하는지 안하는지를 출력

arr=[[0,0,0,0],
     [1,0,1,0],
     [1,0,1,0],
     [0,0,0,0]]  # 0=>길 and 1=>벽
visit=[[0]*4 for _ in range(4)]   # 중복 방지
flag=0 # 도착시 1로 바꿀 예정

def dfs(y,x):
    global flag
    if y==3 and x==3:
        flag=1
        return

    directy=[-1,1,0,0]
    directx=[0,0,-1,1]
    for i in range(4):
         dy=y+directy[i]
         dx=x+directx[i]
         if dy<0 or dx<0 or dy>3 or dx>3: continue  # 배열 범위 벗어나면 안됨
         if visit[dy][dx]==1: continue              # 이미 방문했던 곳이면 안됨
         if arr[dy][dx]==1: continue                # 벽이면 못감
         visit[dy][dx]=1
         dfs(dy,dx)

visit[0][0]=1
dfs(0,0)    # y,x 좌표값
if flag==1:
    print("갈수있습니다.")
else:
    print("도착할수 없습니다.")

# 0,0 -> 1,3 좌표까지 최소 이동 횟수 출력

arr=[[0,0,0,0,1],
     [1,0,1,0,1],
     [1,0,1,0,1],
     [0,0,0,0,0]]
visit=[[0] * 5 for _ in range(4)]

Min=int(21e8)
def dfs(y,x,level):

    global Min
    if y==1 and x==3:
        if level<Min:# 최소레벨 갱신
            Min=level
        return
    directy=[-1,1,0,0]
    directx=[0,0,-1,1]

    for i in range(4):
        dy=y+directy[i]
        dx=x+directx[i]

        if dy<0 or dx<0 or dy>3 or dx>4: continue
        if arr[dy][dx]==1: continue
        if visit[dy][dx]==1: continue

        visit[dy][dx]=1
        dfs(dy,dx,level+1)
        visit[dy][dx]=0

visit[0][0]=1
dfs(0,0,0)  # y,x level-> 이동횟수

print(Min)

2. Stack으로 구현

from collections import deque # deque 패키지 불러오기

def dfs2(graph, start_node):

    visited = []
    need_visited = deque()
    
    #시작 노드 설정해주기
    need_visited.append(start_node)
    
    # 방문이 필요한 리스트가 아직 존재한다면
    while need_visited:
        # 시작 노드를 지정하고
        node = need_visited.pop()
 
        #만약 방문한 리스트에 없다면
        if node not in visited:
 
            # 방문 리스트에 노드를 추가
            visited.append(node)
            # 인접 노드들을 방문 예정 리스트에 추가
            need_visited.extend(graph[node])
                
    return visited

def dfs(start_node):
    stack = [start_node]
    used = []

    while stack:
        node = stack.pop()
        if node not in used:
            used.append(node)
            for i in range(len(arr[node])-1, -1, -1):
                if arr[node][i] == 1:
                    stack.append(i)
    print(used)

arr = [
    [0, 1, 1, 0, 0, 0],
    [0, 0, 0, 1, 1, 0],
    [0, 0, 0, 0, 0, 1],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0]
]

dfs(0)

🎈 stack을 구현할 때 list로 구현하는 것 보다 deque로 구현하는 것이 훨씬 성능면에서 좋다!

DFS 심화 문제

• 프로그래머스 - 여행경로