[알고리즘] 이진 탐색 트리(Binary Search Tree)

이진 탐색 트리(Binary Search Tree)이란?

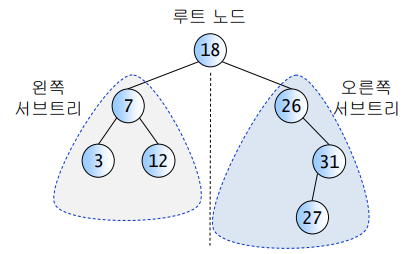
이진 탐색 트리란 다음과 같은 속성을 만족하는 이진 트리 자료구조이다.

• 각 노드에 중복되지 않는 값이 있다.
• 한 노드의 왼쪽 서브 트리는 해당 노드의 값보다 작은 값들을 가진 노드들로 이루어져 있다.
• 한 노드의 오른쪽 서브 트리는 해당 노드의 값보다 큰 값들을 가진 노드들로 이루어져 있다.
• 좌우 서브 트리도 모두 이진 탐색 트리여야 한다.

이진 탐색 트리(BST)의 등장 배경

이진 탐색 : 탐색 시간복잡도 O(logN), 삽입이나 삭제 불가능
연결 리스트 : 탐색 시간복잡도 O(N), 삽입이나 삭제 시 O(1) 소요

이 둘의 장점을 챙긴 자료구조가 이진 탐색 트리이다. 탐색 시 O(logN)의 시간복잡도를 가지며, 자료의 삽입과 삭제도 가능한 자료구조이다.

💡이진 탐색 트리(BST)의 시간 복잡도

빅오 표기법을 기준으로, 만약 타겟 노드가 가장 깊은 레벨에 있다고 하면 높이(h)만큼의 노드를 탐색해야한다.

모든 노드가 빈 자리 없이 채워져 있는 이진 탐색 트리를 포화 이진 탐색 트리라고 하는데, 이렇게 트리가 구성되어있는 경우가 가장 최적의 상황이다. 이 때 노드의 개수를 n이라고 하면

이렇게 되므로 시간복잡도는 O(logn)이 된다.

💡이진 탐색 트리(BST)의 구현

이진 탐색 트리는 간단하게는 1차원 배열로도 표현할 수 있다.

현재 노드의 값과 비교했을 때 삽입되어야 하는 값이 더 작으면 현재 노드의 index에 2를 곱한 곳으로 이동하여 다시 삽입을 시도한다. 더 크면 현재 노드의 index에 2를 곱하여 1을 더한 곳으로 이동하여 시도한다.

BST=[0]*20 # 충분히 길어야할 것
lst=[4,2,9,7,15,1,3] # 트리에 하나씩 삽입될 값들

# tree에 값을 삽입하는 매서드
def insert(target):
    now = 1 # 루트 노드는 0이 아니라 1부터 저장 (index)
    while True:
        if BST[now] == 0:
            BST[now] = target
            return
        if BST[now] < target: now = now*2+1 # target이 현재 노드 값보다 클 때
        else: now = now*2                   # target이 현재 노드 값보다 작을 때

# bst에 특정 값의 존재 여부를 판단하는 매서드
def search(target):
    now = 1
    while True:
        if now >= len(BST): return False  # 배열범위 벗어날 경우
        if BST[now] == 0: return False # 찾고자 하는 값이 없을경우
        if BST[now] == target: return True # 찾았을 경우

        if BST[now] < target: now = now*2+1
        else: now = now*2

# 리스트의 값들을 tree에 저장
for i in range(len(lst)):
    insert(lst[i])

n=int(input())   # 숫자 하나 입력받고
answer=search(n)    # 입력받은 숫자가 존재하는지 search하는 함수
if answer: print("존재")
else: print("존재하지 않음")

BST 심화 구현

BST는 클래스를 정의하여 구현할 수도 있다. 아래 링크를 참고하면 좋다.

[자료구조/Data Structure] 파이썬으로 이진 탐색 트리(Binary Search Tree) 자료구조 알아보기