[알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)

크루스칼 알고리즘(Kruskal Algorithm)이란?

최소 신장 트리를 찾는 데 사용되는 알고리즘 중 하나이다.

1. 신장 트리(Spanning Tree)란?

하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다. 예를 들어 아래와 같은 그래프 G가 있을 때, 이 그래프에서 가능한 신장 트리는 하단의 3가지 그래프이다.

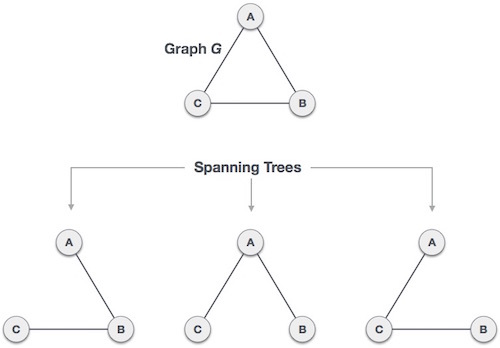
모든 노드들이 연결되어 있지만 사이클이 존재해선 안된다. 이럴 때 우리는 신장 트리라고 하고, 최소 신장 트리는 간선의 가중치가 존재할 때 그 가중치들의 합이 최소가 될 때의 트리를 최소 신장 트리라고 한다. 즉, 최소 비용으로 만들 수 있는 신장 트리를 최소 신장 트리라고 한다.

2. 크루스칼 알고리즘의 동작 과정💡

• 비용을 기준으로 오름차순으로 정렬한다. (비용이 적은 것부터 연결하기 위해)
• 간선의 개수만큼 for문 돌리면서 union해준다.
  • 그룹화 할 대상이 다른 그룹이면 그룹화 해주고 비용을 더한다.
  • 이미 같은 그룹이라면 그냥 넘어간다.
  • 그룹화 성공이 (정점의 개수 - 1)이면 멈춰준다.

크루스칼 알고리즘은 그리디 알고리즘으로 분류된다. 먼저 모든 간선에 대하여 정렬을 수행한 뒤, 가장 비용이 적은 간선부터 집합에 포함시키므로, 항상 최적의 해를 보장할 수 있다.

3. 크루스칼 알고리즘의 시간 복잡도

간선의 개수가 E개일 때, O(E*log*E)의 시간 복잡도를 가진다. 왜냐하면 크루스칼 알고리즘에서 시간이 가장 오래 걸리는 부분은 간선을 정렬하는 작업이며, 이 과정의 시간 복잡도가 O(ElogE)이기 때문이다. 크루스칼 내부에서 사용되는 서로소 집합 알고리즘의 시간 복잡도는 정렬 알고리즘의 시간 복잡도보다 작으므로 무시한다.

💡구현 코드

N = int(input()) # 정점의 개수
M = int(input()) # 간선의 개수
graph = [list(input().split()) for _ in range(M)] # 간선의 정보 입력

graph.sort(key=lambda x: int(x[2]))

arr = [0]*200

def findboss(target):
    if arr[ord(target)]==0:
        return target
    ret=findboss(arr[ord(target)])
    arr[ord(target)] = ret # 최적화
    return ret

def union(x,y):
    global arr

    fx,fy = findboss(x), findboss(y)
    if fx == fy: return False         # 이미 같은 그룹일 때 그룹화 실패
    arr[ord(fy)] = fx
    return True

cnt, sum = 0, 0
for i in range(M):
    if union(graph[i][0], graph[i][1]): # 그룹화 성공
        cnt += 1
        sum += int(graph[i][2])
        if cnt >= N-1:
            break
print(sum)

'''
입력
5       #정점의개수
8       #간선의개수
C D 1   #간선의 정보 입력
A C 3
C E 5
A E 7
A B 9
B D 11
B C 14
A D 20

출력
18      #최소 비용
'''

💡크루스칼 알고리즘 활용 문제

• SWEA
  • 최소 신장 트리