문제 1. 괄호 문제


중간에 이미 완성되어 있는 부분은 최대한 건드리지 않고, 이외의 부분만 수정해보자
--> 이미 완성되어 있는 부분은 색칠해봄
- 괄호문자열의 길이가 홀수면 불가능 -> -1 출력
- 짝수라면 '(의 개수' A와 ')의 개수' B가 몇이더라도 두 번 이내로 가능하다.
올바른 괄호 문자열의 성질
뒤집어도 올바른 괄호문자열이다
괄호문제를 쉬운 문제로 변형하는 방법
올바른 괄호 문자열은 뒤집어도 어차피 영향을 받지 않으므로, 올바른 문자열은 지우고 연산해도 무관하다.
하나의 기준선을 기준으로 왼쪽은 다 닫는 괄호, 오른쪽은 다 여는 괄호
왜?
))))()(((
이런 경우일 경우, 올바른 괄호문자열로 ()이 빠진다.
구현방법
STACK


여는 괄호는 다 스택에 push,
닫는 괄호가 나오면
1. 스택에 원소가 있으면 pop
2. 아니면 변형

- 쉬운 문제유형으로 변형한 뒤
- 다 뒤집어주자

문제 2. 롤러코스터

가장 작은 최종 속력은 -> 가장 작은 최종 속력을
- a와 b는 1~10억까지의 정수이다.
- N은 1 ~ 100,000까지의 정수
마지막에 속력값이 가장 최소로 나오게끔 하는 레일을 배치하면 될까?

실제로 배치 방법을 정하고 값을 구하는 것 자체가 불가능!! (가짓수가 너무 많다)
정답 배치의 성질



i는 1~(n-1)까지 다 만족하는 수

분자가 0이 될 수 있는데, 상관없고 그냥 내림차순 정렬해주면 된다.
정렬방법은 마음대로 - 선택정렬, 삽입정렬, 병합정렬, 힙정렬, ...
정렬을 굳이 절대적인 숫자(값)으로 해야할까? No!
주어진 배열에서 요소들 간의 잘 정의된 순서(Cycle이 없는 순서)가 있으면 두 요소 사이의 비교식을 통해 전체를 정렬할 수 있다. ( ((ai+1) - 1)bi <= ((ai -1)(bi+1) )
문제 3. 최대 부분합

누적합 배열 사용!!
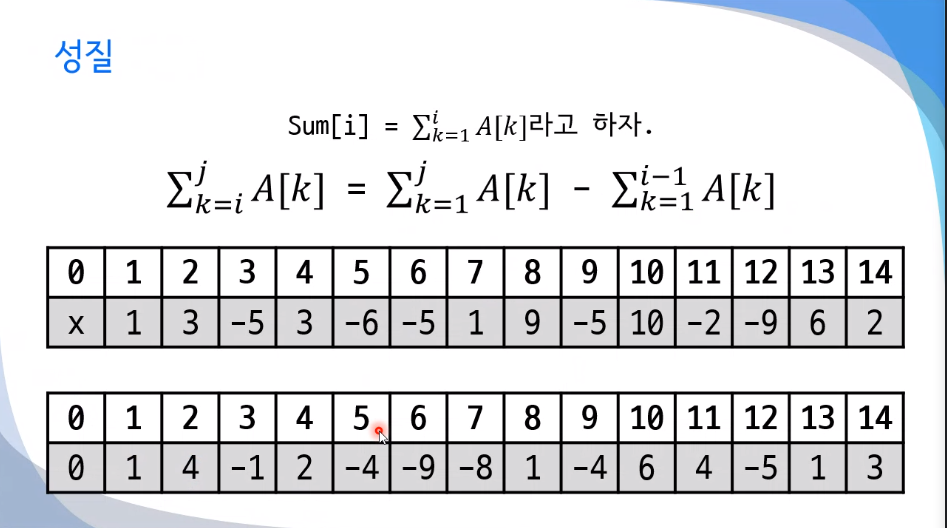
시간복잡도 : O(n)
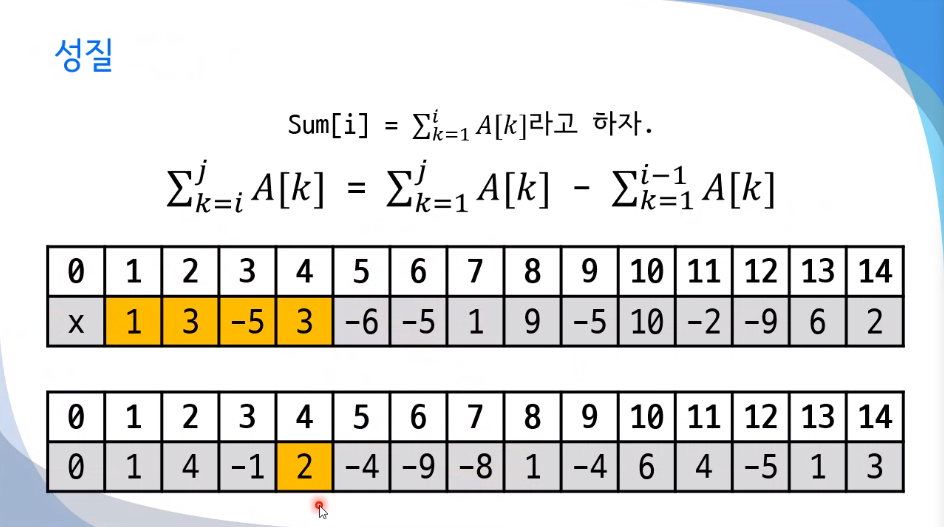
특정 구간의 합을 구하려면?
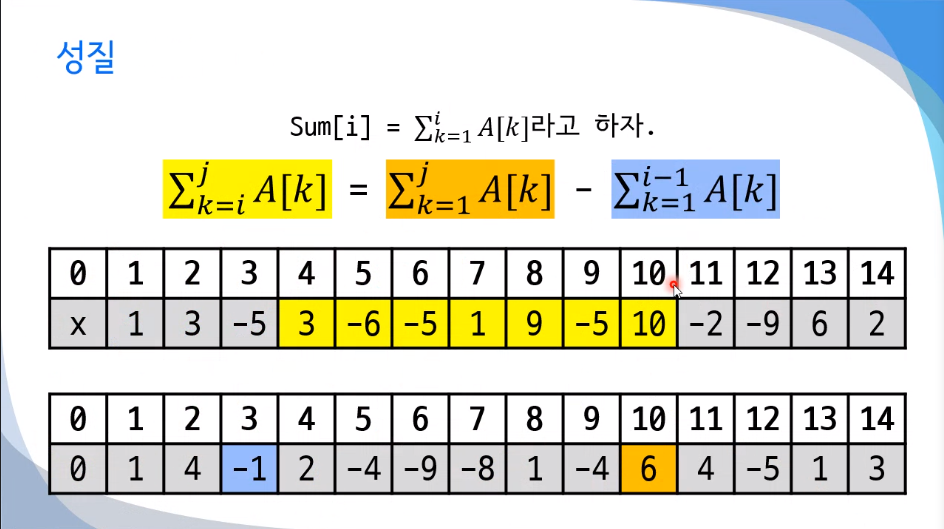
시간복잡도

최대 부분합
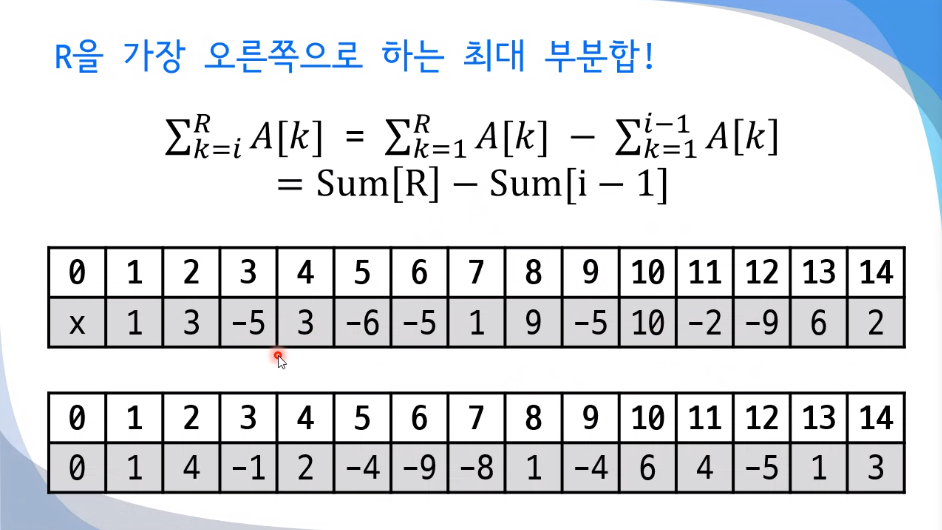
우리가 원하는 알고리즘 연산 --> 중복된 연산을 줄이는 것!
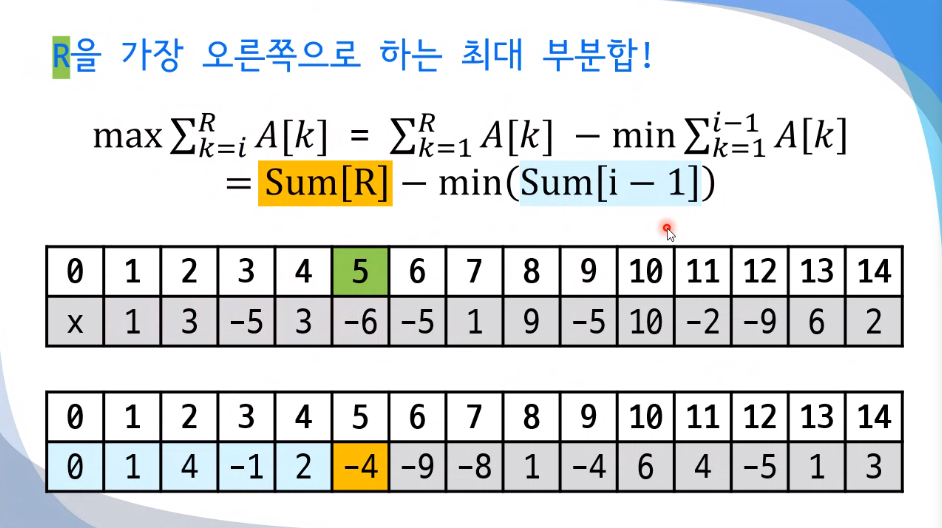
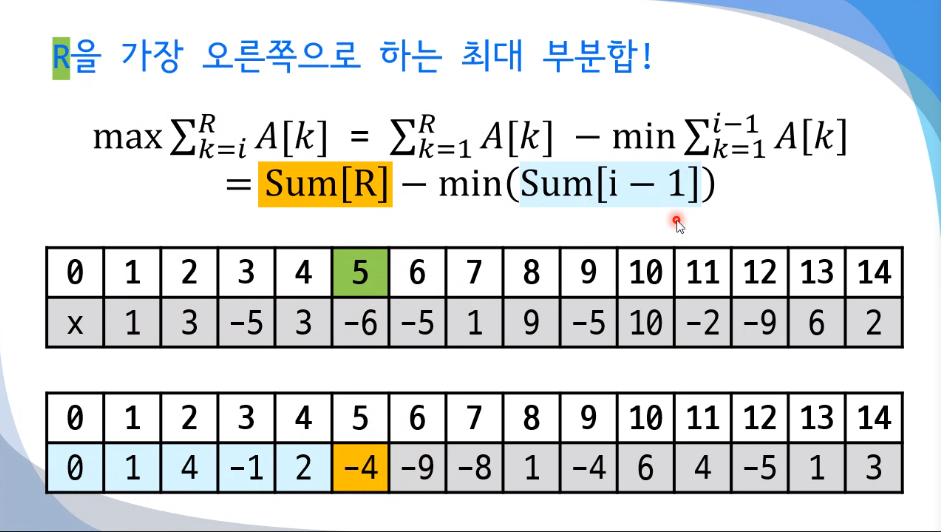
여기서, 최솟값을 이미 찾아놨는데 R이 하나 늘어난다면 처음부터 해당범위까지 최솟값을 구하는 연산을 다시 해야함 --> 중복!!
최솟값을 찾는 과정을 더 개선해보자
최솟값 탐색 개선책 (Cache 배열 사용)
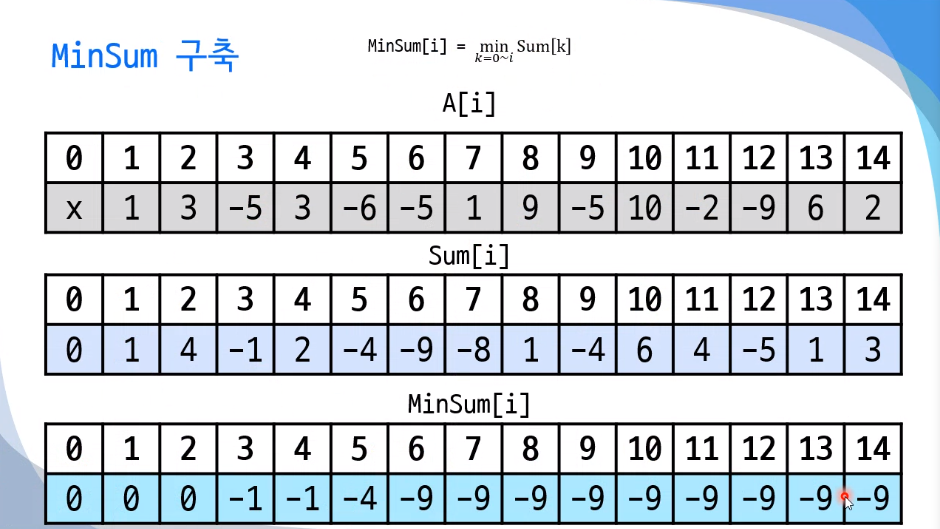
시간복잡도 : O(n)
문제 4. 두 번 이상 등장하며 가장 긴 서브문자열
(Samsung 스타일 - 알고리즘 중시/문자열 좋아함)
빡센 구현문제

• S의 최대 길이 : 100,000
해시

해시충돌이 필연적이다. 최대한 문자열이 다르면 결과값이 다를 확률을 높이는 형태. 같으면 같다고 믿자.

문자열의 해시값을 구하는 방식
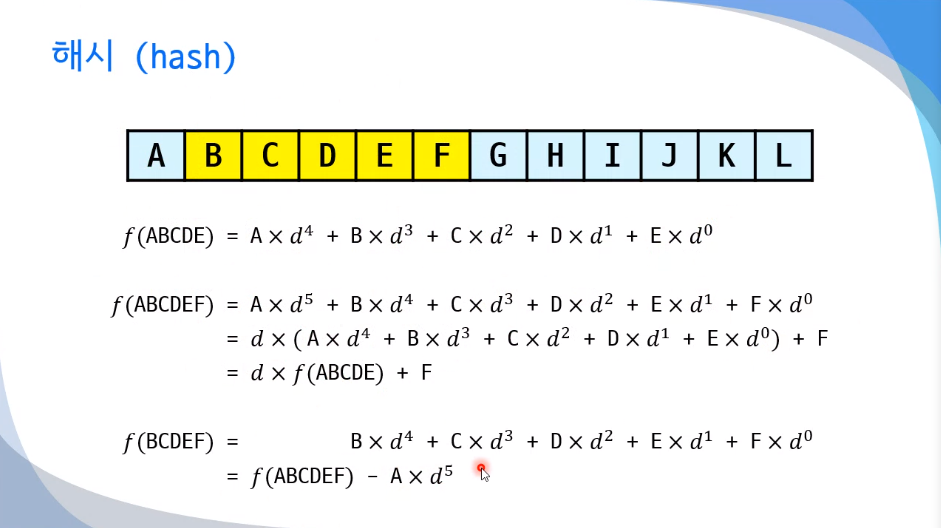

위 연산을 사용해도 나머지는 동일하다. (나눗셈만 하지 않으면 나머지는 동일하다)
다시 문제로 돌아가서, 문제를 쉽게 풀어내면

길이문제 -> 판정문제로 변형
Yes -> 길이 반환
No -> -1 반환
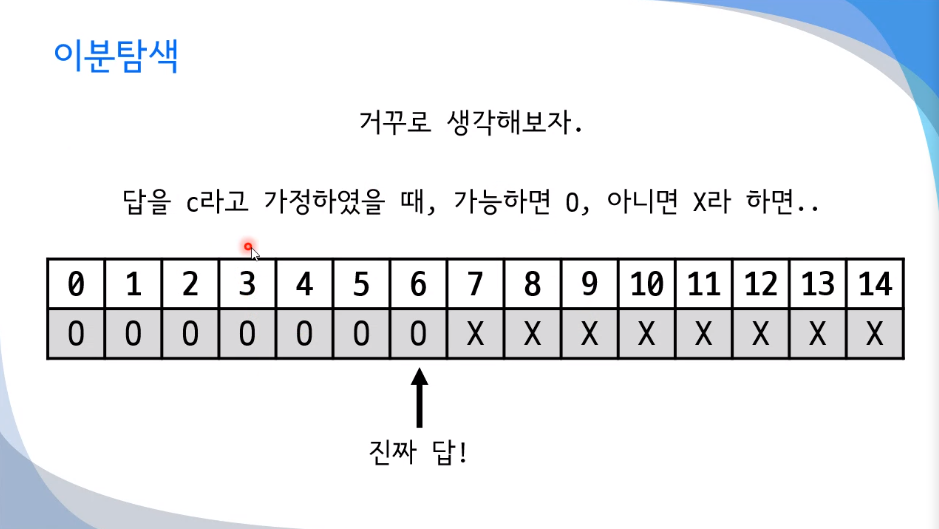
어떠한 한 칸에 대해서,
X -> 그보다 긴 길이는 모두 불가능
O -> 그보다 작은 길이 모두 가능
시간복잡도 = O(N log^2 N) - 힙정렬, 병합정렬 등


O(n)의 시간복잡도로 풀 수 있는 방법

부록.

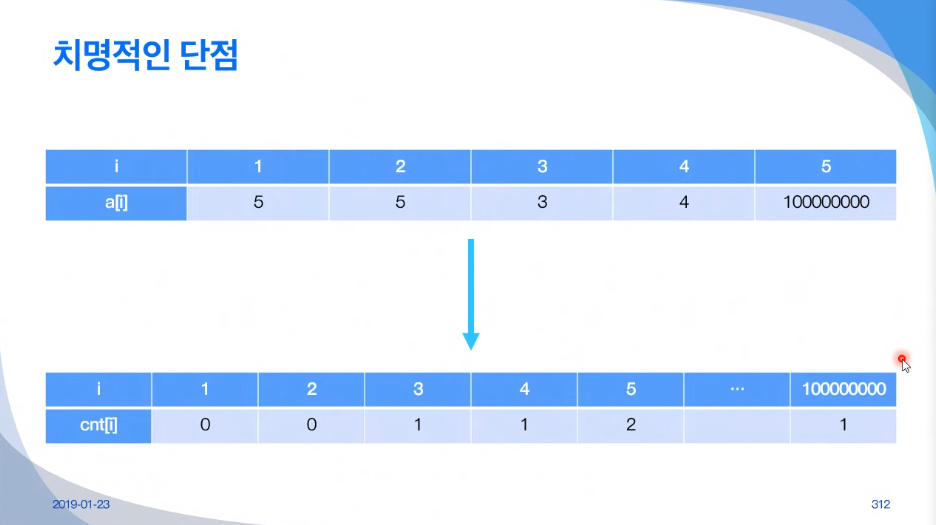
1. COUNTING SORT

1. 개수 세기
2. 누적합 구하기
3. 역순으로 자리지정하기
(이전에 정리했던 파일 보기)
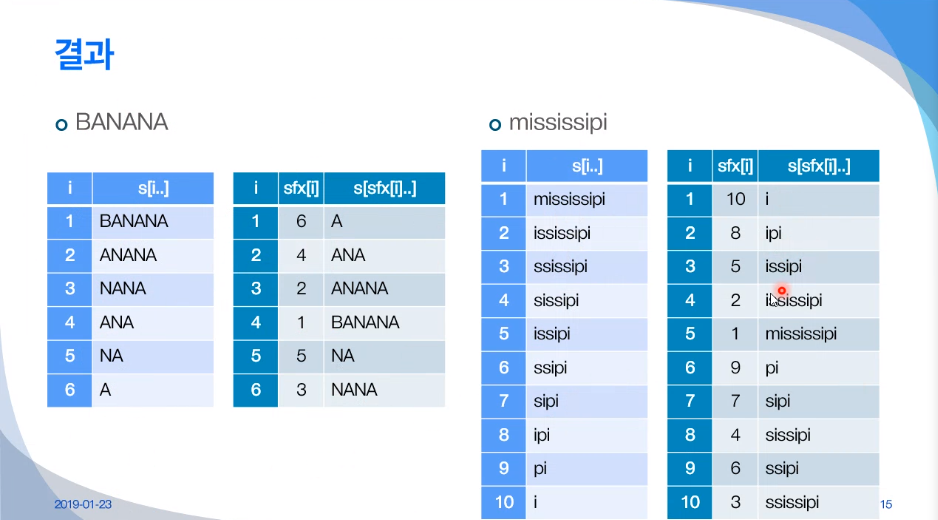
2. SUFFIX ARRAY(접미사 배열)
: 문자열의 모든 접미사를 모아 정렬한 배열