백준 2108번을 풀던 중 중앙값과 최빈값을 구하는 과정에서 계수 정렬을 쓰게 됐는데, 개념을 좀 확실하게 잡고 싶어서 정리해본다.
🤔 계수 정렬이란?
계수 정렬은 데이터들의 크기에 따라 정렬해주는 정렬 알고리즘으로,
기존 선택 정렬, 삽입 정렬 등에 비해 시간복잡도가 O(n)으로 빠른 정렬 알고리즘이다.
지금까지의 정렬은 크기에 따라 데이터의 위치를 바꿔가며 정렬을 했다면,
계수 정렬은 위치를 굳이 바꾸지 않고 단순히 크기에만 기준을 맞춰 갯수를 세준다. 또한 데이터에 각 한번씩만 접근하면 되기 때문에 다른 정렬보다 효율적이다.
😏 계수 정렬 과정
그림으로 차근차근 설명해보겠다. 먼저 다음과 같은 배열이 있다고 가정하자.

1. arr 순회하며 갯수 세기
해당 arr를 순회하며, 해당 값을 인덱스로 갖는 새로운 배열(counting)을 생성하여 1씩 증가시킨다.
예를 들면,
- arr[0] = 5이므로 counting[5]++
- arr[1] = 1이므로 counting[1]++
위의 과정을 수행하면 다음과 같은 결과가 나온다.

결국 counting은 각 데이터의 개수를 담고 있는 배열이 된다.
2. counting의 누적합 구하기
counting의 각 값을 차례대로 더해가며 누적합을 구해간다.
과정을 그림으로 나타내면 다음과 같다.








📌 결론
 여기까지 하면 우리는 위의 두 배열을 얻게 된다.
여기까지 하면 우리는 위의 두 배열을 얻게 된다.
💡 배열 counting의 각 값은, 곧 생성될 배열 result의 (해당 인덱스 - 1)을 나타낸다.
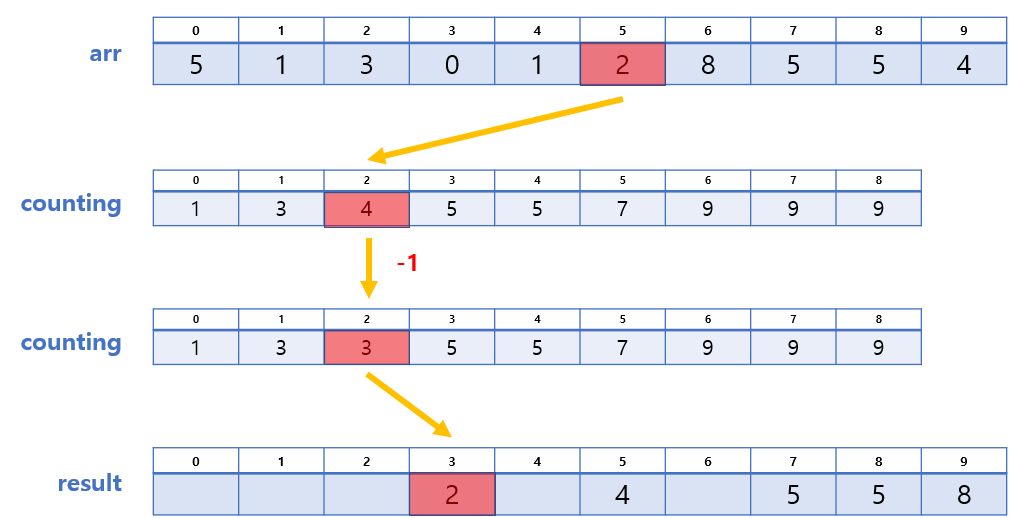
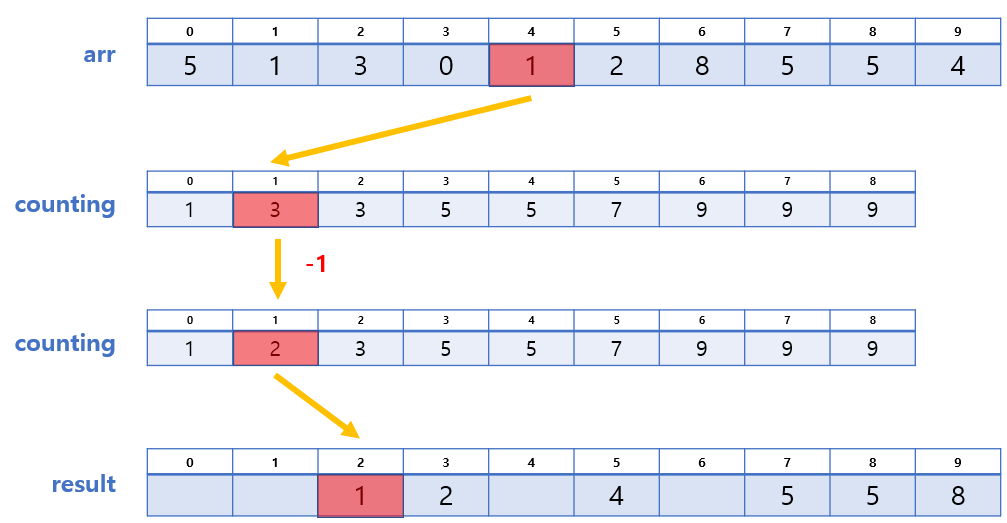
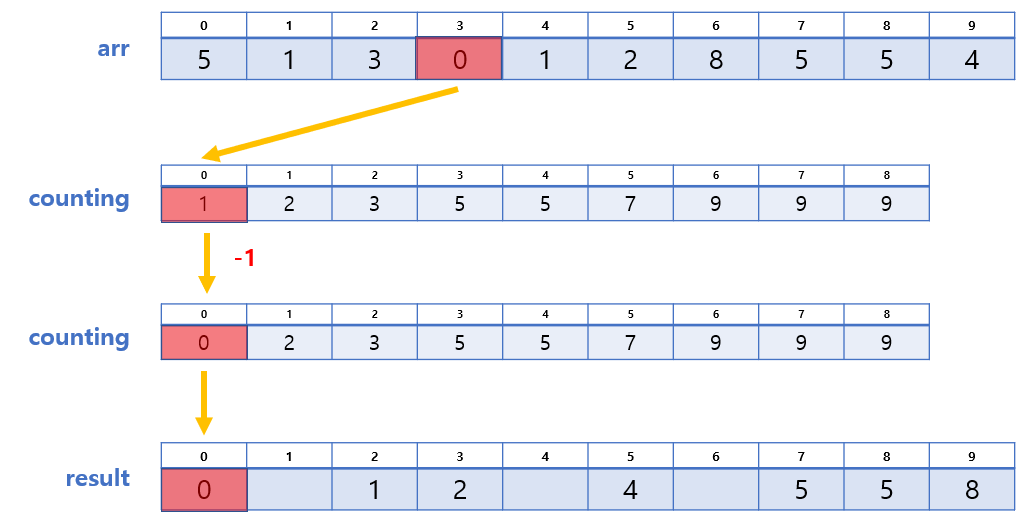
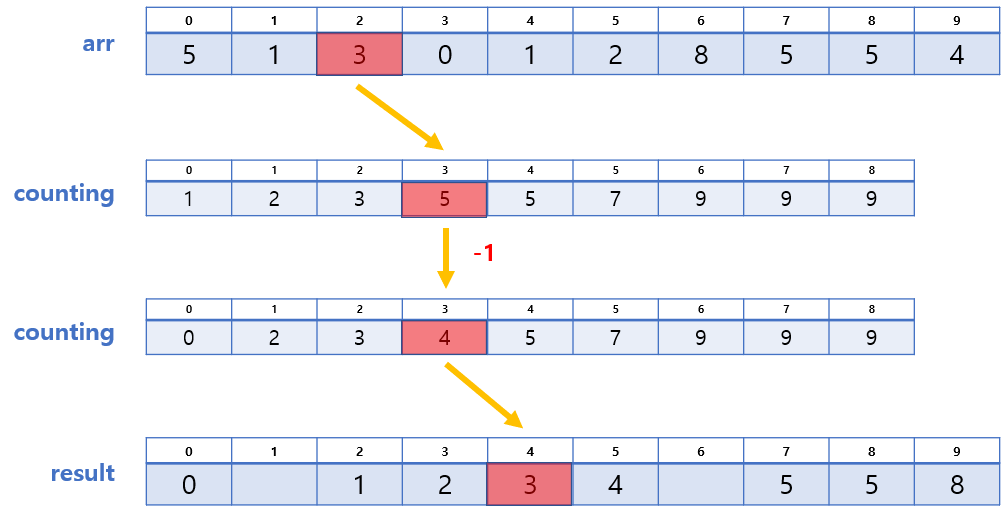
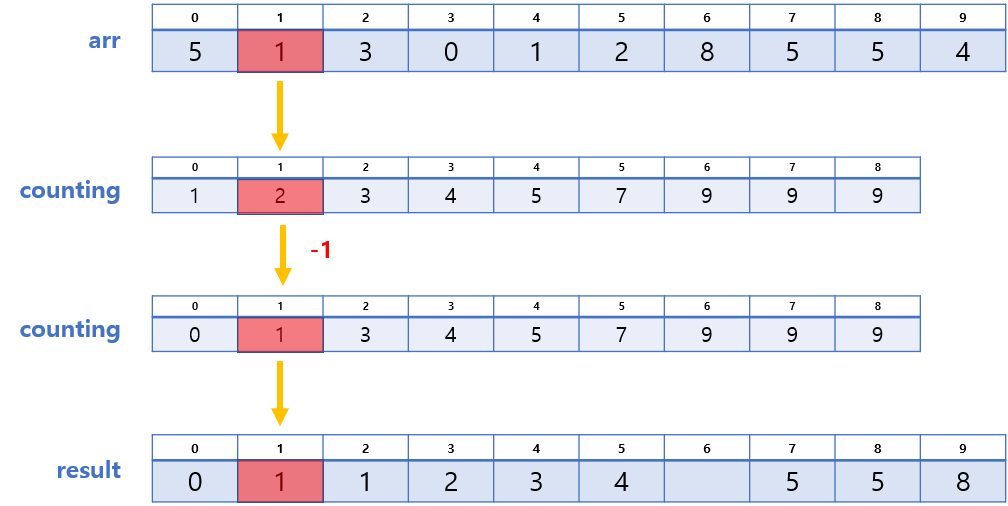
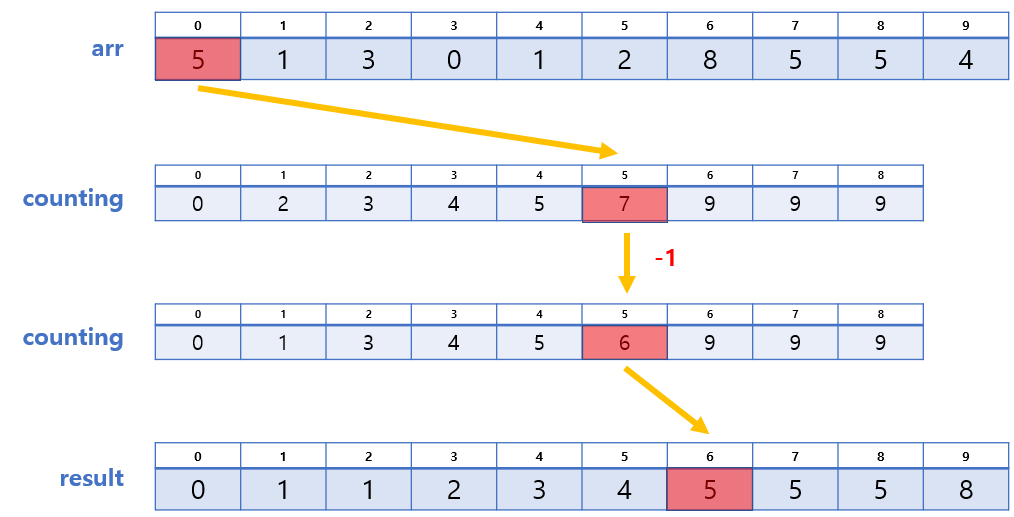
3. counting의 각 값에 대응하는 위치에 배정하기
우리는 과정 2에서 생성된 arr와 counting 배열을 활용하여 result 배열에 최종적으로 배열할 것이다.
방법은 다음과 같다.
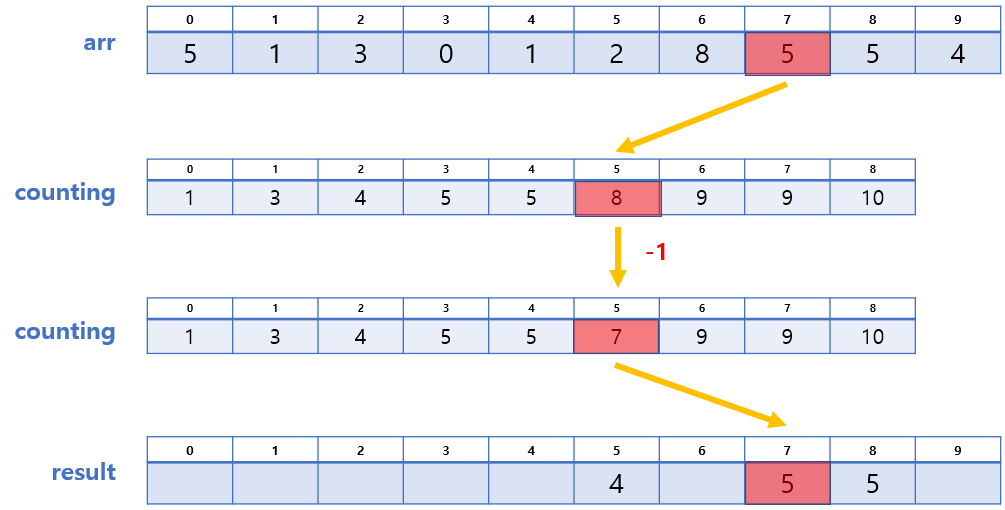
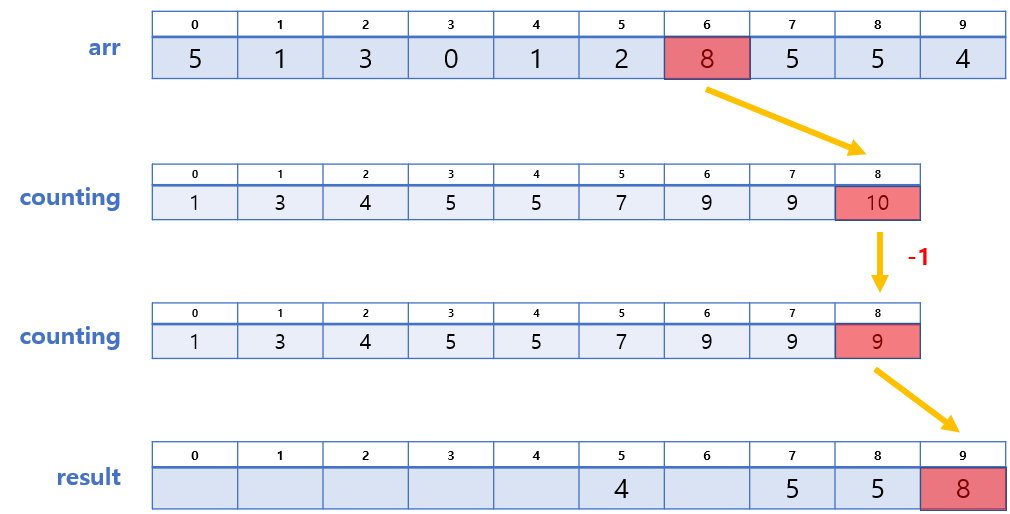
- arr의 값을 찾는다. (A라 하자)
- counting에서 인덱스가 A인 곳의 값을 찾는다. (B라 하자)
- result[B-1]에 A를 넣는다.
- counting[A], 즉 B의 값을 1 감소 시킨다.
방법에 대한 예시를 들자면 이렇다.
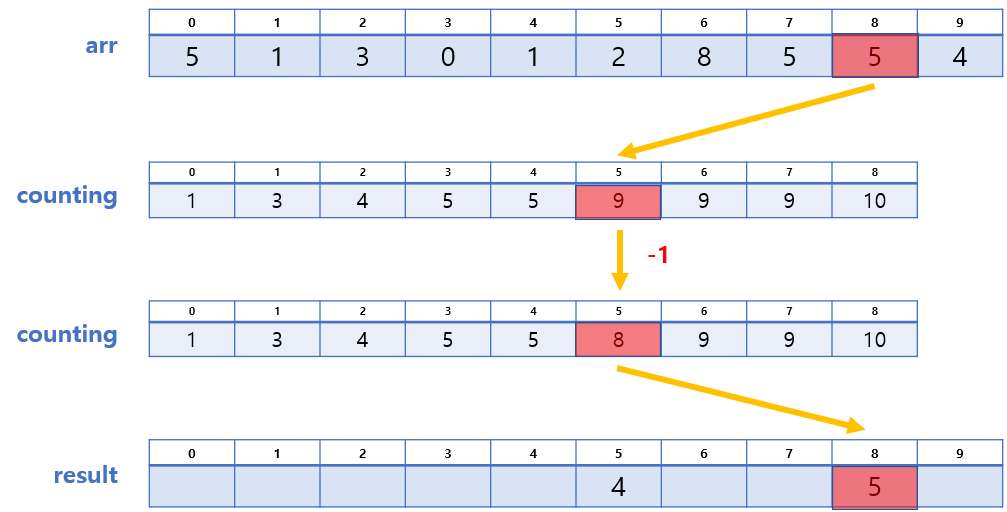
- arr[9] = 4 → counting[4] = 6 → result[6-1] = 4,
counting[4]의 값에서 1 감소 - arr[8] = 5 → counting[5] = 9 → result[9-1] = 5,
counting[5]의 값에서 1 감소 - ...
❗ 단, arr의 마지막부터 순회해야 안정적이다!
이 과정 또한 그림으로 설명하며 진행하는 편이 나을 것 같아, 그림을 보며 이해해보자.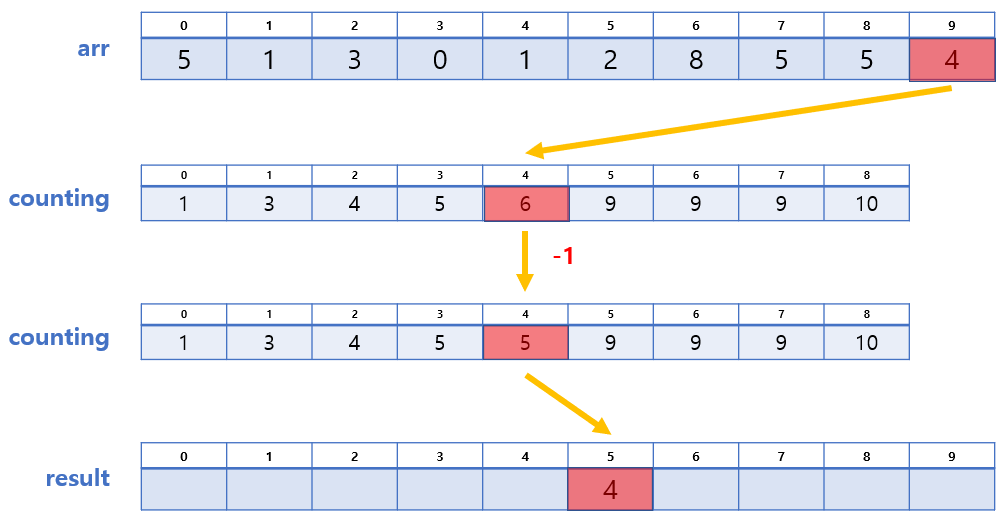
📌 결론

이렇게 과정 3까지 마치고 나면 위와 같이 정렬된 배열을 얻게 된다.
이 알고리즘 자체가 두 수를 비교하는 과정이 없기 때문에, 다른 정렬 알고리즘보다 비교적 성능이 좋다. 다만 단점도 존재한다.
counting이라는 배열을 새로 생성해줘야한다.
정수 데이터의 범위가 적다면 문제없지만, 만약 데이터의 개수가 10개인데 범위가 0~1억이라면 그만큼의 크기를 가진 배열 counting을 선언해줘야 하기 때문에 메모리 낭비가 심하다.
따라서 이 정렬 알고리즘은 상황에 따라 적절하게 사용해야 한다. 만약 메모리가 너무 낭비될 예정이라면 퀵 정렬이나 병합정렬 등이 더욱 효율적일 수 있다.
참고)
https://blog.naver.com/ndb796/221228361368
https://st-lab.tistory.com/104?category=892973

