[python] 피보나치 수 구하기

피보나치 수 구하기

첫째, 둘째 항이 1이고 그 뒤의 항은 바로 앞 두 항의 합인 수열
1, 1, 2, 3, 5, 8, 13, ...

재귀함수 사용

$f(n) = f(n-1) + f(n-2)$ 이기 때문에 가장 먼저 생각해 볼 수 있는 방법은 재귀함수로 구현.

예를 들어, F(5)를 구한다고 할 때 재귀함수로 구현하면,

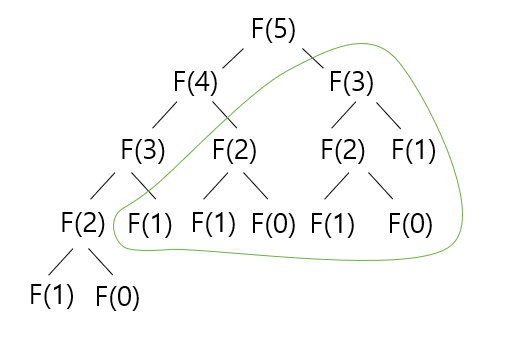
이미 계산했던 부분이 계속 반복적으로 호출되는 것을 확인할 수 있다. N이 커지면 커질 수록 시간복잡도, 공간복잡도가 커짐.

✅ 시간 복잡도: $O(2^n)$ (해당 트리의 높이만큼)
✅ 공간 복잡도: $O(2^n)$

반복문 사용

다음 항을 계산하고, 현재 항과 다음 항을 저장하는 것을 반복.

n = int(input())
a = b = sum = 1

for i in range(3, n+1):
  sum = a + b;
  a = b;
  b = sum;

✅ 시간 복잡도: $O(N)$
✅ 공간 복잡도: $O(1)$