Algorithm Complexity - Insertion Sort 중심으로

Chapter2 Getting Started & Chapter3 Growth of Function

Insertion Sort(삽입 정렬)

• 이미 정렬된 배열과 비교하여 숫자 하나의 자리를 찾아 넣어주는 정렬

• InsertionSort (A, n) {
  	for i = 2 to n {
      	key = A[i]
          j = i-1;
          while (j>0) and (A[j]>key) {
          	A[j+1] = A[j]
              j = j+1
          }
          A[j+1] = key
       }
    }
  

• 위의 코드는 큰 수가 앞으로 오게 정렬되고(내림차순) key가 계속 배열의 제일 앞 숫자보다 더 큰 수가 올 때 best case

  • 이 경우 complexity는 O(n)
  • worst case의 complexity는 O($n^2$)
    

• 작은 수가 앞에 오게 정렬하는 경우 (오름차순)

  • 자료구조에 따라 complexity가 다름
    1. array
       • best case : O($n^2$)
         • key가 항상 가장 작은 값이 들어갈 경우도 array는 기존의 배열에서 값을 옮기는 작업을 해야하기 때문
       • worst case : O($n^2$)
         
    2. linked-list
       • best case : O($n$)
       • worst case : O($n^2$)

Upper Bound Notation

O($n$)

• $f(n) <= c * g(n)$ for all $n >= n_0$
  - $c$와 $n_0$은 실수
  
• ex) $f(n) = 3n^2 + 8$이라고 할 때, $c$가 4이고 $n_0$이 3이라고 할 때, $3n^2 + 8 <= 4n^2$ for all $n >= 3$

Lower Bound Notation

$\Omega(n)$

• $0 <= c * g(n) <= f(n)$ for all $n >= n_0$
• ex) $f(n) = 3n^2 + 8$이라고 할 때, $c$가 2이고 $n_0$이 1이라고 할 때, $0 <= 3n^2 + 8 <= 2n^2$ for all $n >= 1$

Asymptotic Tight Bound

$\Theta(n)$

• $c_1 g(n) <= f(n) <= c_2g(n)$ for all $n >= n_0$
• ex) 위의 예에서 $f(n) = 3n^2 + 8$는 $\Theta(n^2)$임을 알 수 있다.

Other Asymptotic Notations

$o()$ is like <
$\omega()$ is like >

소문자는 등호가 빠진다.

지수함수가 complexity로 나온 경우 그 알고리즘은 못쓴다고 생각하면 됨

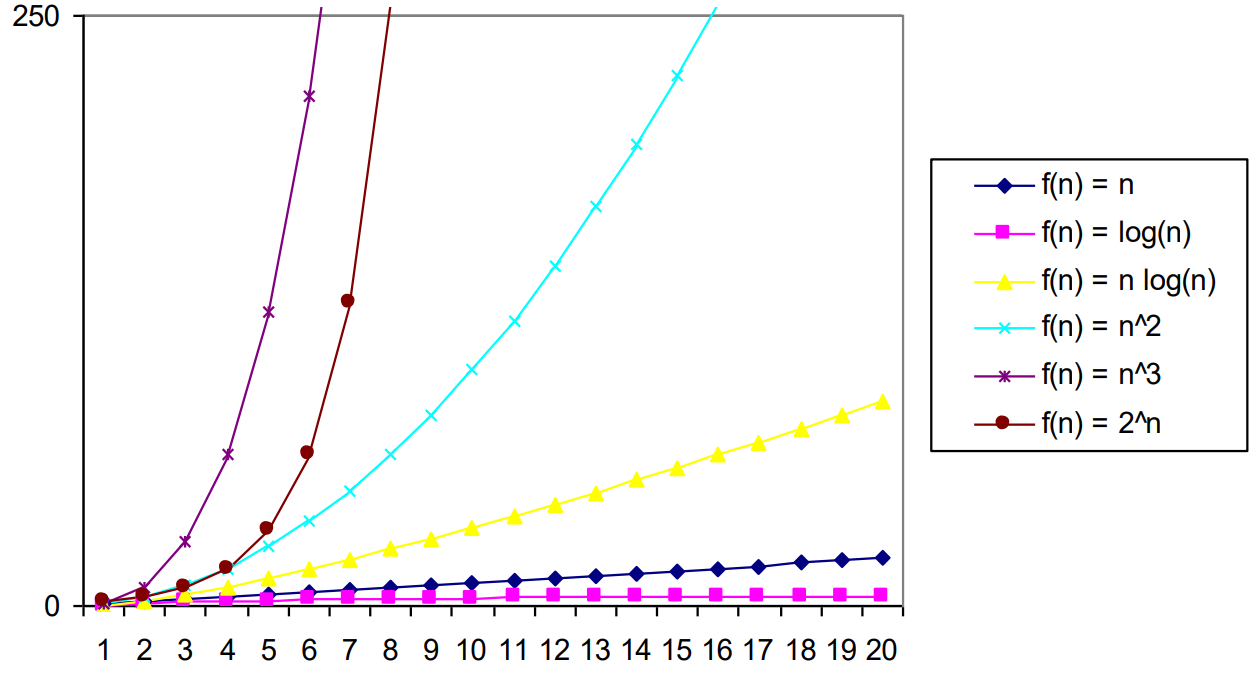
오늘은 첫 수업이라 알고리즘 복잡도의 복습정도인 것 같다.
다음 수업 리뷰는 3시 안에 끝낼 수 있도록 해야겠다.