Chapter 4 Divide-and-Conquer

Merge Sort(병합 정렬)

• 정렬해야 할 배열을 절반씩 나누어(Divide) 각각 정렬한 후 합친다.

• MergeSort(A, left, right) {                        
  	if (left < right) {                           
      	mid = floor((left + right) / 2);
          MergeSort(A, left, mid);
          MergeSort(A, mid+1, right);
          Merge(A, left, mid, right); 
      }
  }

• 1번 줄의 MergeSort()의 Effort는 $T(n)$이며 4번,5번 줄의 MergeSort()의 Effort는 $T(n/2)$이다.
  Merge()의 Effort는 $\Theta(n)$이다.
  그 외의 줄은 constant Effort를 가진다.

• 이를 점화식(Recurrence)으로 나타내면
  

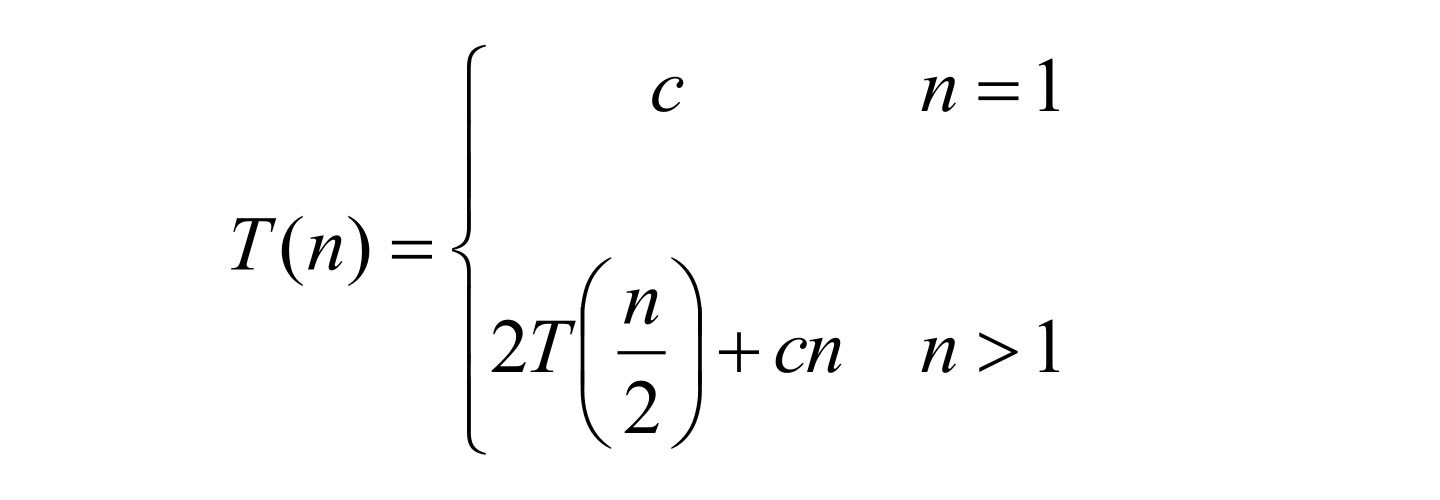
• 풀이과정
  

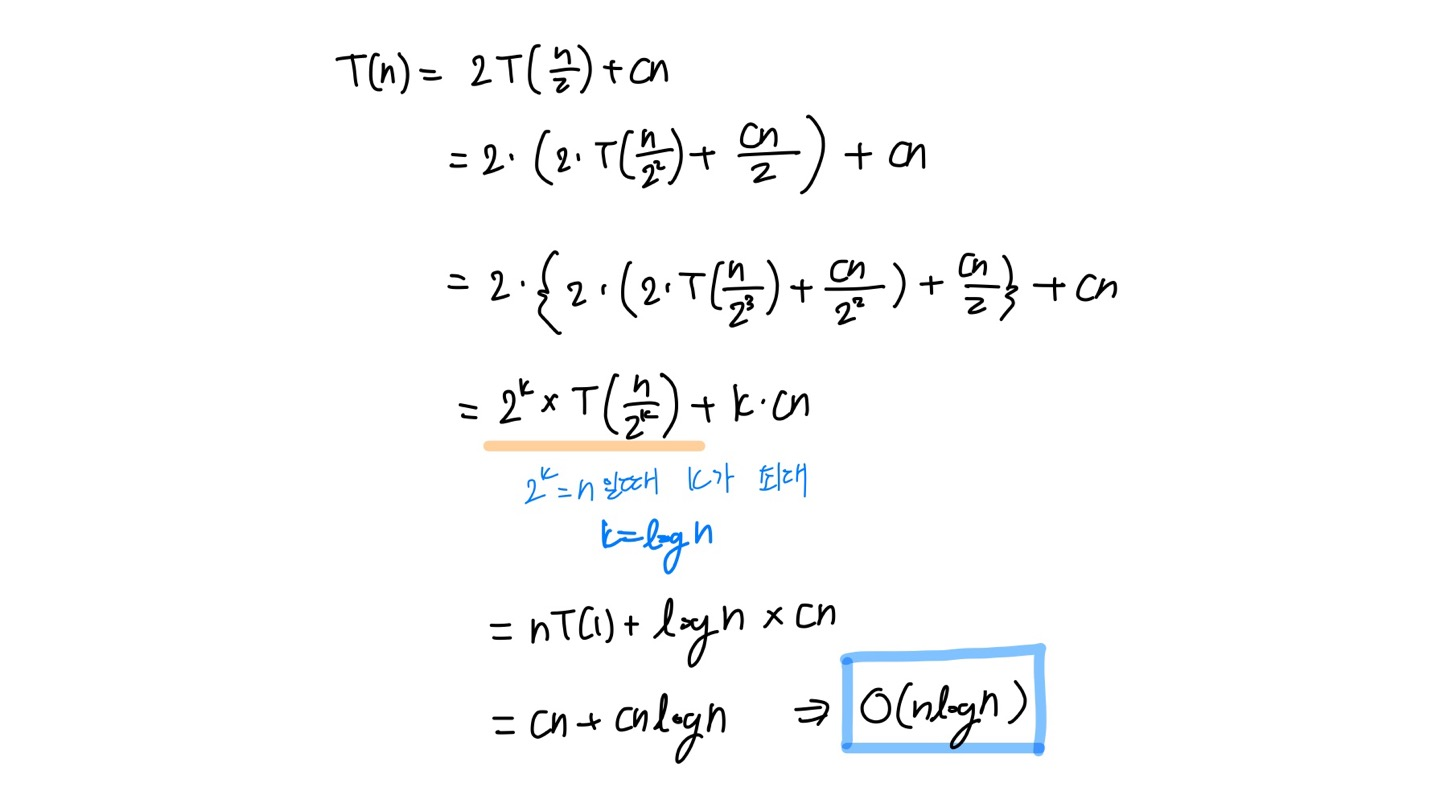
• 점화식을 푸는 방법

  • Substitution method (대입법) -> 찍기
    • Masking a good guess method
  • Iteration (recursion-tree) method -> 수식에 대한 일반식을 찾아내는 것
  • Master method -> 공식으로 풀기
    • If $T(n) = aT(n/b) + f(n)$일 때
      

Heaps

• 힙의 조건

  1. complete binary tree (full과 헷갈리지 x)
  2. min heap - parent node <= child node
     max heap = parent node >= child node

• heaps are usually implemented as arrays without information loss

  • complete binary tree이기 때문

• Root node가 $A[1]$인 경우

  • Node $i$ = $A[i]$
  • The parent of node $i$ = $A[i/2]$
  • The left child of node $i$ = $A[2i]$
  • The right child of node $i$ = $A[2i+1]$

• heap height => $logn$

Heapity()

• complete binary tree에서 heap으로 만들기 위해 노드의 순서를 조정하는 과정
• 전체를 한번에 조정하는 것이 아니라 divide and conquer로 힙 2개를 만들고 하나로 합한다고 생각한다.

• Heapify(A, i) {
  	l = Left(i); r = Right(i);
      if (l <= heap_size(A) && A[l] > A[i])  
          //첫 번째 조건:child가 2개보다 적을수도 있어서
      	largest = l;
      else 
      	largest = i;
      if (r <= heap_size(A) && A[r] > A[largest])
      	largest = r;
      if (largest != i)
      	Swap(A, i, largest);
          Heapify(A, largest);
  }

• Heapify()의 시간복잡도는 $O(logn)$이다.

BuildHeap()

• BuildHeap(A) {
  	heap_size(A) = length(A);
      for (i = length[A]/2 downto 1) 
      //leaf node때문에 절반 건너뛰고 시작
      	Heapify(A, i);
  }

• Heapify는 노드 1개에 대한 코드이고 BuildHeap은 Heapify를 n번 수행하는 것이다.
• sudo code를 보면 BuildHeap()의 시간 복잡도가 $O(nlogn)$인것 같지만 트리의 절반이 leaf node이기 때문에 다시 생각해볼 필요가 있다.
• 타이트한 시간 복잡도는 $O(n)$이다.

HeapSort

• Max Heap으로 root노드를 찾은 후 root노드와 최하단의 leaf node를 바꾼다. 바꾼 leaf node는 없는 셈 치고 root node에서 Heapify를 부르는 과정을 반복해 오름차순의 정렬을 얻는 방법.

• HeapSort(A) {
  	BuildHeap(A);                  //O(n)
      for (i = length(A) downto 2) { //O(n)
      	Swap(A[1], A[i]);          
          heap_size(A) -= 1;
          Heapify(A, 1);             //O(logn)
      }
  }    

• HeapSort의 시간복잡도는 $O(nlogn)$

• MergeSort와 HeapSort 비교

  • HeapSort가 더 좋은 점
    • extra space를 요구하지 않는다.
      • mergesort는 n개의 extra space를 요구한다.
  • MergeSort가 더 좋은 점
    • stable하다

      데이터의 value가 같을 때 직전의 선후관계를 유지하는 것을 stable하다고 한다. 예로는 excel이 있다.

    • in-memory 알고리즘이 아닌 disk-based 알고리즘으로 바꾸기 용이하다.

      • in-memory
        • 메인 메모리에 모든 데이터가 저장되어 있고 disk를 백업용으로 사용한다.
        • memory(RAM)이 disk보다 빠르기 때문에 in-memory 방식이 더 좋다.
      • disk-based
        • 모든 데이터를 disk에 저장하고 메모리를 caching에 사용한다.

Priority Queues

• 들어간 순서에 상관 없이 weight가 높은 값이 먼저 나온다.
• Heap 데이터구조는 priority queue를 구현하기 매우 용이하다.
• operation
  • Insert()
  • Maximum()
  • ExtractMax()

QuickSort

• MergeSort를 in place버전으로 바꾼 것

  in-place 정렬
  - 원소들의 개수에 비해 충분히 무시할 만한 저장공간만을 더 사용하는 정렬 알고리즘

• divide and conquer 알고리즘이다.
  • A[p..r] 배열을 A[p..q]와 A[q+1..r]로 나누어 정렬한다.
• 시간 복잡도
  • average case : $O(nlogn)$
  • worst case : $O(n^2)$
• 사람들이 quick sort를 많이 사용하는 이유
  1. worst case가 쉽게 발생하지 않는다.
  2. merge, heap sort에 비해 cache friendly하다.
     • 옆의 값과 비교가 많이 일어나기 때문이다.
  • 이로 인해 실질적인 성능이 훨씬 좋아진다.

    cache friendly
    - 캐쉬는 지역성(locality)를 가지는데 이는 데이터에 대한 접근이 시간적, 공간적으로 가깝게 발생하는 것을 말한다. 캐시의 적중률(Hit rate)을 극대화하여 캐시가 효율적으로 동작하기 위해 사용되는 성질이다.
    (참고 : https://rebro.kr/180)
    - 직접적인 핸들링은 하기 힘들지만 알고리즘이 캐쉬 메모리를 얼마나 유용하게 쓰는가가 성능에 영향을 미친다.

• QuickSort(A, p, r) {
  	if (p < r) {
     	q = Partition(A, p, r); //q는 pivot value 자리
         QuickSort(A, p, q-1);
         QuickSort(A, q+1, r);
       }
    }
    
   Partition(A, l, r) {
    	p = A[r]; 
      i = l;
      j = r - 1;
      while (TRUE) {
      	while A[i] <= p
    	     	i++;
          while A[j] > p
          	j--;
          if (i < j)
          	Swap(A, i, j);
          else 
          	Swap(A, i, r);
               return i;
              

• worst case
  • $T(1) = \Theta(1)$
  • $T(n) = T(n-1) + \Theta(n)$
  • 따라서 $T(n) = \Theta(n^2)$
• best case
  • $T(n) = 2T(n/2) + \Theta(n)$
  • 따라서 $T(n) = \Theta(nlogn)$
• (자세한 시간복잡도 풀이 과정은 ppt참고)