Insertion sort

---

1. Sorting problem

• input : a sequence of n numbers (keys) $\lang$$a_1$, $a_2$, $\cdots$ , $a_n$$\rang$
• output : a permutation $\lang$$a_1^\prime$, $a_2^\prime$, $\cdots$ , $a_n^\prime$$\rang$ of the input sequence such that $a_1^\prime$ $\le$ $a_2^\prime$ $\le$ $\cdots$ $\le$ $a_n^\prime$

2. Pseudocode

• 분명하고 간결한 method로 given algorithm을 명시
• algorithm의 essence를 간결하게 전달하기 위해 대부분의 software engineering 관련 issues를 무시

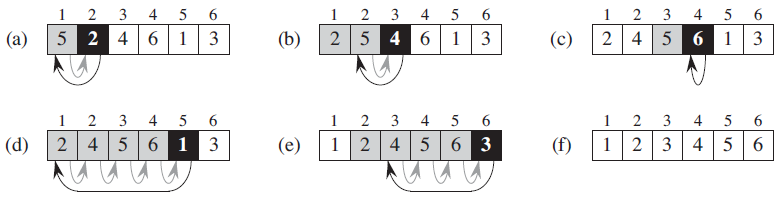
3. Procedure and operation

• parameter로 array $A[1\,.\,.\,n]$을 받는 INSERTION-SORT의 procedure
  

• array $A = \lang5, 2, 4, 6, 1, 3\rang$일 때 INSERTION-SORT의 operation
  

Loop invariants and the correctness of insertion sort

1. Loop invariant

• algorithm의 loop에서 각 iteration 전 또는 후에 항상 true인 property
• INSERTION-SORT에서 lines 1-8의 $A[1\,.\,.\,j - 1]$를 만드는 loop의 loop invariants

	1. 처음 parameter로 들어왔을 때 A[1 .. j - 1]의 elements로 구성돼 있다
	2. 순서대로 정렬돼 있다

• algorithm의 correctness를 이해하기 위해 사용한다

2. Initialization, Maintenance, Termination

• loop invariant를 보이기 위한 세 가지
  1. Initialization : 첫 번째 iteration전에 true
  2. Maintenance : iteration전에 true이면, 다음 iteration전에도 true
  3. Termination : loop가 종료됐을 때, invariant는 algorithm의 correctness를 보일 수 있는 유용한 property를 제공

3. The correctness of insertion sort

• Initialization
  $j = 2$일 때, $A[1\,.\,.\,j - 1]$은 $A[1]$이다. $A[1]$의 element는 parameter로 처음 들어올 때 $A[1]$의 element와 같다. 그리고 $A[1]$은 정렬돼 있다. 따라서 첫 번째 iteration전의 loop invariant은 true이다.
• Maintenance
  lines 4-7에서 $A[j]$의 element는 proper position을 찾을 때 까지 $A[j-1]$, $A[j-2]$, $A[j-3]$, .. 로 이동한다. line 8에서 $A[j]$의 element를 삽입한다. 그러면 $A[1\,.\,.\,j - 1]$는 초기의 $A[1\,.\,.\,j - 1]$의 elements로 이루어져 있고 정렬된 상태가 된다. 따라서 $j$의 increment가 이루어진 후 다음 iteration시작 전 $A[1\,.\,.\,j - 1]$은 loop invariant를 만족한다. loop variant의 true는 유지된다.
• Termination
  for loop의 종료 condition은 $j > A.length = n$이고 iteration하면서 $j$는 1씩 증가하기 때문에 언젠간 $j = n + 1$돼 반드시 종료된다. loop invariant의 $j$를 $n + 1$로 치환해보면, 초기 $A[1\,.\,.\,n]$의 elements로 정렬된 $A[1\,.\,.\,n]$를 종료 후 얻게 된다. 이 때 $A[1\,.\,.\,n]$은 전체 array의 elements를 정렬한 것이므로, insertion sort는 correct algorithm이다.