[백준] 1647번: 도시 분할 계획

문제

동물원에서 막 탈출한 원숭이 한 마리가 세상구경을 하고 있다. 그러다가 평화로운 마을에 가게 되었는데, 그곳에서는 알 수 없는 일이 벌어지고 있었다.

마을은 N개의 집과 그 집들을 연결하는 M개의 길로 이루어져 있다. 길은 어느 방향으로든지 다닐 수 있는 편리한 길이다. 그리고 각 길마다 길을 유지하는데 드는 유지비가 있다. 임의의 두 집 사이에 경로가 항상 존재한다.

마을의 이장은 마을을 두 개의 분리된 마을로 분할할 계획을 가지고 있다. 마을이 너무 커서 혼자서는 관리할 수 없기 때문이다. 마을을 분할할 때는 각 분리된 마을 안에 집들이 서로 연결되도록 분할해야 한다. 각 분리된 마을 안에 있는 임의의 두 집 사이에 경로가 항상 존재해야 한다는 뜻이다. 마을에는 집이 하나 이상 있어야 한다.

그렇게 마을의 이장은 계획을 세우다가 마을 안에 길이 너무 많다는 생각을 하게 되었다. 일단 분리된 두 마을 사이에 있는 길들은 필요가 없으므로 없앨 수 있다. 그리고 각 분리된 마을 안에서도 임의의 두 집 사이에 경로가 항상 존재하게 하면서 길을 더 없앨 수 있다. 마을의 이장은 위 조건을 만족하도록 길들을 모두 없애고 나머지 길의 유지비의 합을 최소로 하고 싶다. 이것을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 집의 개수 N, 길의 개수 M이 주어진다. N은 2이상 100,000이하인 정수이고, M은 1이상 1,000,000이하인 정수이다. 그 다음 줄부터 M줄에 걸쳐 길의 정보가 A B C 세 개의 정수로 주어지는데 A번 집과 B번 집을 연결하는 길의 유지비가 C (1 ≤ C ≤ 1,000)라는 뜻이다.

임의의 두 집 사이에 경로가 항상 존재하는 입력만 주어진다.

출력

첫째 줄에 없애고 남은 길 유지비의 합의 최솟값을 출력한다.

입출력 예제

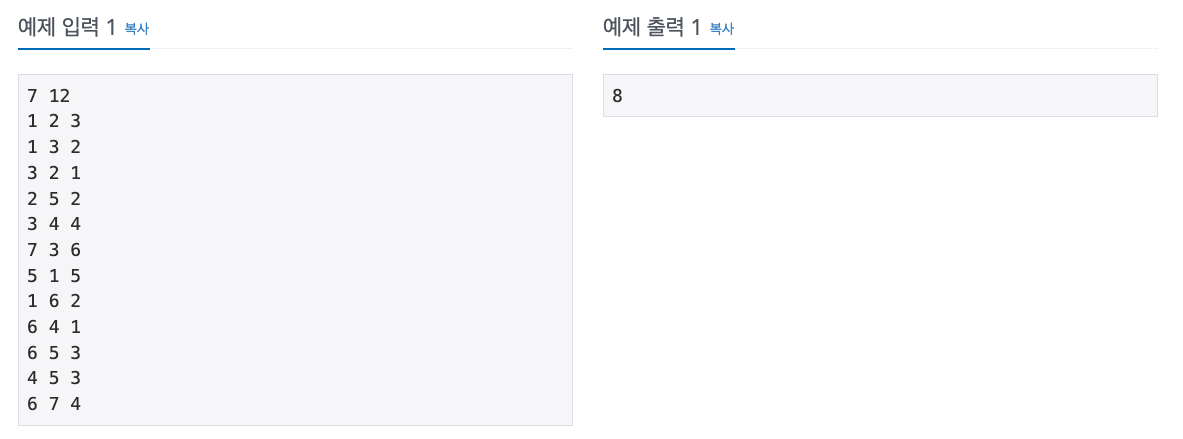
풀이

크루스칼 알고리즘을 활용한 풀이
크루스칼 알고리즘을 실행해서 최소 스패닝 트리를 구한다.
만들어 내면서 사용된 엣지들중 가중치가 가장 큰 것을 구해뒀다가
모든 가중치의 합에서 가중치의 합이 가장 큰 것을 뺀 값을 결과 값으로 출력한다.

V, E = map(int, input().rstrip().split(" "))
graph = []

for _ in range(E):
    start, end, weight = map(int, input().rstrip().split(" "))
    graph.append((weight, start, end))


def find(cur, parent):
    if parent[cur] == cur:
        return cur
    else:
        return find(parent[cur], parent)


def union(start, end, parent):
    start_root = find(start, parent)
    end_root = find(end, parent)

    if start_root < end_root:
        parent[end_root] = start_root
    else:
        parent[start_root] = end_root
    return


def kruskal(V, E, graph):
    graph.sort(key=lambda data: -data[0])
    answer = 0
    max_weight = 0
    parent = [v for v in range(V + 1)]
    while graph:
        weight, start, end = graph.pop()
        if find(start, parent) == find(end, parent):
            continue
        answer += weight
        union(start, end, parent)
        max_weight = max(max_weight, weight)


    return answer - max_weight


def solution(V, E, graph):
    print(kruskal(V, E, graph))
    return


solution(V, E, graph)