[백준] 1922번: 네트워크 연결

문제

도현이는 컴퓨터와 컴퓨터를 모두 연결하는 네트워크를 구축하려 한다. 하지만 아쉽게도 허브가 있지 않아 컴퓨터와 컴퓨터를 직접 연결하여야 한다. 그런데 모두가 자료를 공유하기 위해서는 모든 컴퓨터가 연결이 되어 있어야 한다. (a와 b가 연결이 되어 있다는 말은 a에서 b로의 경로가 존재한다는 것을 의미한다. a에서 b를 연결하는 선이 있고, b와 c를 연결하는 선이 있으면 a와 c는 연결이 되어 있다.)

그런데 이왕이면 컴퓨터를 연결하는 비용을 최소로 하여야 컴퓨터를 연결하는 비용 외에 다른 곳에 돈을 더 쓸 수 있을 것이다. 이제 각 컴퓨터를 연결하는데 필요한 비용이 주어졌을 때 모든 컴퓨터를 연결하는데 필요한 최소비용을 출력하라. 모든 컴퓨터를 연결할 수 없는 경우는 없다.

입력

첫째 줄에 컴퓨터의 수 N (1 ≤ N ≤ 1000)가 주어진다.

둘째 줄에는 연결할 수 있는 선의 수 M (1 ≤ M ≤ 100,000)가 주어진다.

셋째 줄부터 M+2번째 줄까지 총 M개의 줄에 각 컴퓨터를 연결하는데 드는 비용이 주어진다. 이 비용의 정보는 세 개의 정수로 주어지는데, 만약에 a b c 가 주어져 있다고 하면 a컴퓨터와 b컴퓨터를 연결하는데 비용이 c (1 ≤ c ≤ 10,000) 만큼 든다는 것을 의미한다. a와 b는 같을 수도 있다.

출력

모든 컴퓨터를 연결하는데 필요한 최소비용을 첫째 줄에 출력한다.

입출력 예제

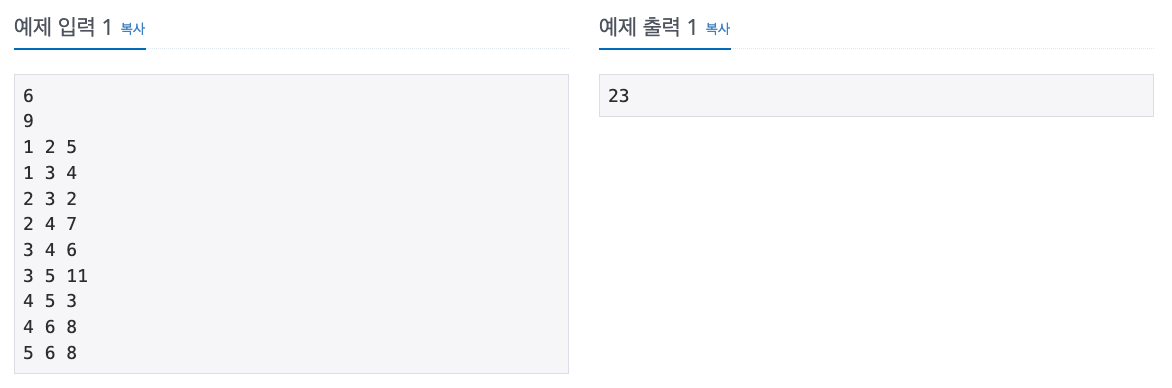
풀이

크루스칼 알고리즘을 활용한 풀이

V = int(input())
E = int(input())
graph = []
for _ in range(E):
    start, end, weight = map(int, input().rstrip().split(" "))
    graph.append((start, end, weight))


def find(cur, parent):
    if parent[cur] == cur:
        return cur
    else:
        return find(parent[cur], parent)


def union(start, end, parent):
    start_root = find(start, parent)
    end_root = find(end, parent)

    if start_root < end_root:
        parent[end_root] = start_root
    else:
        parent[start_root] = end_root


def kruskal(V, E, graph):
    parent = [v for v in range(V + 1)]
    graph.sort(key=lambda data: -data[2])
    answer = 0
    while graph:
        start, end, weight = graph.pop()
        if find(start, parent) == find(end, parent):
            continue
        answer += weight
        union(start, end, parent)

    return answer


def solution(V, E, graph):
    print(kruskal(V, E, graph))
    return

solution(V,E,graph)