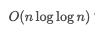[백준] 에라토스체네스의 체

문제

에라토스테네스의 체는 N보다 작거나 같은 모든 소수를 찾는 유명한 알고리즘이다.

이 알고리즘은 다음과 같다.

2부터 N까지 모든 정수를 적는다.
아직 지우지 않은 수 중 가장 작은 수를 찾는다. 이것을 P라고 하고, 이 수는 소수이다.
P를 지우고, 아직 지우지 않은 P의 배수를 크기 순서대로 지운다.
아직 모든 수를 지우지 않았다면, 다시 2번 단계로 간다.
N, K가 주어졌을 때, K번째 지우는 수를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N과 K가 주어진다. (1 ≤ K < N, max(1, K) < N ≤ 1000)

출력

첫째 줄에 K번째 지워진 수를 출력한다.

입출력 예제

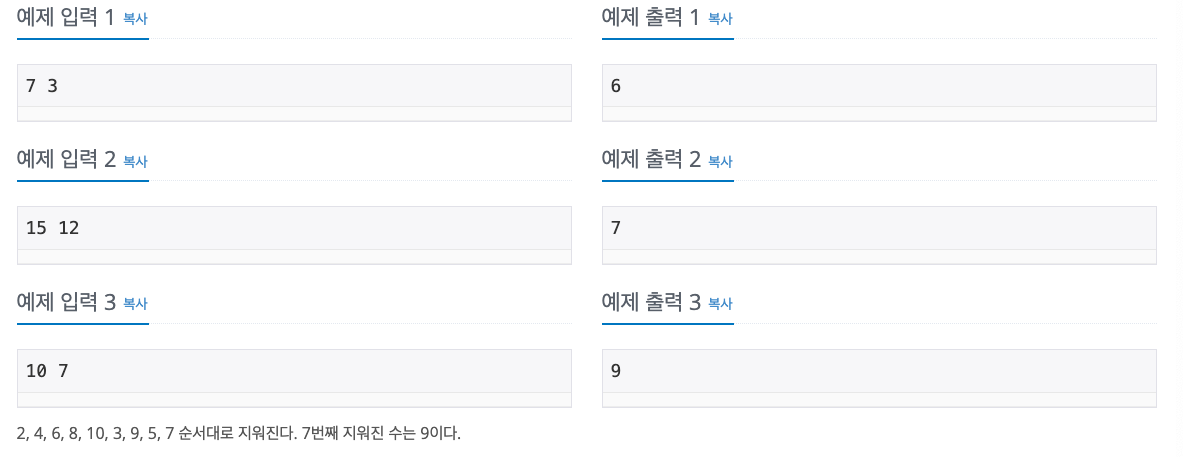
풀이

N+1(0 포함) 크기의 boolean 배열을 만든다.
지워진 경우 True를 저장하고 안지워진 경우 False를 저장한다.

배열을 인덱스 2부터 순회하면서
False인 경우
인덱스 배수의 인덱스 값을 지운다.

K 번째 지운 수를 출력하고 종료한다.

우리가 원래 알던대로 소수를 구하는 알고리즘을 사용하면 O(N^2) 가 소요되는데
에라토스테네스의 체 알고리즘을 사용하면

만큼 소요된다.

https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes#Algorithm_complexity

N, M = map(int, input().split(" "))

def solution(N, M):
    is_del = [True, True] + [False] * (N - 1)

    count = 0
    for target in range(2, len(is_del)):
        for index in range(target, len(is_del), target):
            if not is_del[index]:
                is_del[index] = True
                count += 1
                if count == M:
                    return index

print(solution(N, M))