Today What I Learned

Javascript를 배우고 있습니다. 매일 배운 것을 이해한만큼 정리해봅니다.

---

Algorithm : N-Rooks & N-Queens

1. N-Rooks & N-Queens: n * n의 체스판에 룩(Rook)과 퀸(Queen)을 충돌 없이n개 배치하는 알고리즘이다.
2. 체스 룰은 이번에 정확히 배웠는데,
   룩(Rook)은 본인이 위치한 자리를 기준으로 가로줄과 세로줄에 말이 있을 때(충돌이 있을 때) 해당 말을 공격할 수 있다.
   퀸(Queen)은 룩보다 더 활동 범위가 넓어서 본인이 위치한 자리를 기준으로 가로, 세로, 양 대각선에 말이 있다면(충돌이 있을 때) 해당 말을 공격 & 자리 이동을 할 수 있다.
3. 의사코드(Pseudo Code)를 통해 어떻게 문제를 해결해 나갈지 전략(?) 혹은 계획을 세운 후 실제로 코딩을 진행하는 연습을 진행했다.
   이 알고리즘에서 해결 방법은 룩과 퀸이 가진 고유의 조건에 기반해 원하는 배치(n개의 룩/퀸 두기)를 성공하는 것이라고 보면 된다.

1. 조각 내어 생각하기

1. 먼저 룩은 자신의 위치를 기준으로 행(row)이나 열(column)에 다른 말이 있으면 안 된다. 따라서 row conflict를 체크하는 함수와 column conflict를 체크하는 함수가 필요하다.
2. 퀸의 경우에는 룩에서 만든 2개의 함수에 좌상측 대각선(major diagonal)과 우상측 대각선(minor diagonal)에서 conflict check가 필요하다. 총 4개의 검사가 한 번에 이뤄져야 한다.

• 1개 row conflict 체크

hasRowConflictAt: function(rowIndex) {
      let obj = this.attributes;

      let count = 0;
      for (let i = 0; i < obj[rowIndex].length; i++) {
        count = count + obj[rowIndex][i];
      }
      return count > 1;
}

• n * n 체스판에서 n 개 row conflict 체크

hasAnyRowConflicts: function() {
      let obj = this.attributes;
      for (let key in obj) {
        if (this.hasRowConflictAt(key)) {
          return true;
        }
      }
      return false;
    }

• column conflict 체크

hasColConflictAt: function(colIndex) {
      let obj = this.attributes;
      let count = 0;
      for (let i = 0; i < obj[0].length; i++) {
        count = count + obj[i][colIndex];
      }
      return count > 1
    }

• n * n 체스판에서 n 개 column conflict 체크

hasAnyColConflicts: function() {
      let obj = this.attributes;

      for (let i = 0; i < obj[0].length; i++) {
        if (this.hasColConflictAt(i)) {
          return true;
        }
      }
      return false;
}

• 행, 열 충돌을 확인하는 함수를 완성하고 나면 그 다음 양 대각선에 대한 충돌을 확인하는 함수를 만들어야 한다.
  이 때 행, 열과 달리 대각선은 검사의 시작점이 상이하다. 가장 작은 대각선부터 체스판 내 모든 대각선을 검사해야 하므로 아래와 같은 방법으로 시작점을 체스판 바깥에서부터 시작하는 방법을 선택했다.
  처음엔 헷갈려서 이렇게 그림을 그려보니 좀 더 명확해졌다. (파란색은 major, 빨간색은 minor diagonal)
  

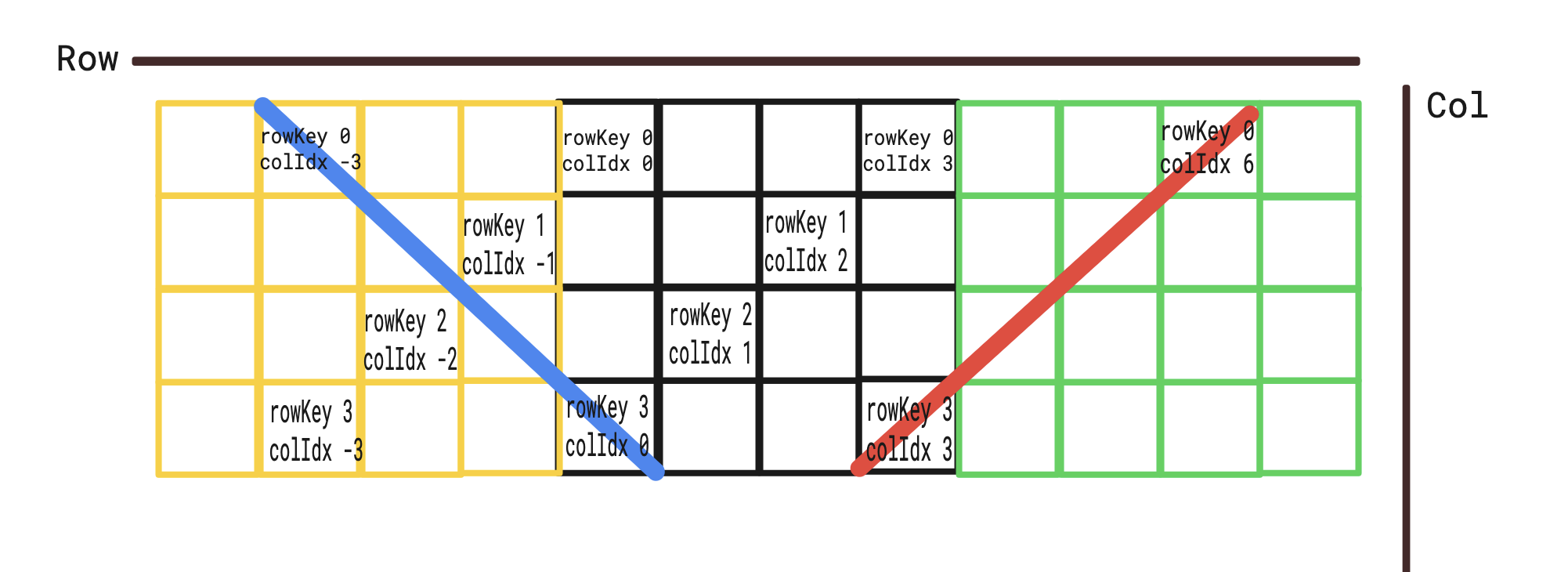
• major diagonal conflict 체크

hasMajorDiagonalConflictAt: function(colIdx) {
      let obj = this.attributes;
      let count = 0;

      for (let i = 0; i < obj[0].length && colIdx < obj[0].length; i++, colIdx++) {
        if (obj[i][colIdx] === 1) {
          count++;
        }
      }
      return count > 1
}

• n * n 체스판에서 n 개 major diagonal conflict 체크

hasAnyMajorDiagonalConflicts: function() {
      let obj = this.attributes;
      if (Object.keys(obj).length === 0) {
        return false;
      }

      let n = obj[0].length;

      for (let colIdx = -(n - 1); colIdx < n + (n - 1); colIdx++) {
        if (this.hasMajorDiagonalConflictAt(colIdx)) {
          return true;
        }
      }
      return false;
    }

• minor diagonal conflict 체크

hasMinorDiagonalConflictAt: function(colIdx) {
      let obj = this.attributes;
      let count = 0;
      let n = obj[0].length;
  
      for (let i = n - 1; i >= 0 && colIdx < n; i--, colIdx++) {
        if (obj[i][colIdx] === 1) {
          count++;
        }
      }
      return count > 1
}

• n * n 체스판에서 n 개 minor diagonal conflict 체크

hasAnyMinorDiagonalConflicts: function() {
      let obj = this.attributes;
      if (Object.keys(obj).length === 0) {
        return false;
      }

      let n = obj[0].length;

      for (let colIdx = -(n - 1); colIdx < n + (n - 1); colIdx++) {
        if (this.hasMinorDiagonalConflictAt(colIdx)) {
          return true;
        }
      }
      return false;
    }

2. 조각을 조합하기

1. 이제 조각 내었던 conflict check를 조합하면서 충돌이 없는 상태를 유지하면서 n * n 개의 체스판에 n개의 룩/퀸을 배치해야 한다.
2. 체스판을 표현할 구조는 배열 속 배열로 보면 된다.

• ex) [[1,0,0,0], 2번row, 3번row, 4번row]
• row의 위치는 배열의 index로 보고, column의 위치는 nestedArr의 index로 본다.

3. 가장 먼저 n * n의 빈 체스판을 구현해야 한다.

• ex) 4 * 4 체스판이라면 빈 체스판을 [[0,0,0,0], [0,0,0,0], [0,0,0,0], [0,0,0,0]]로 표현

4. 배열의 0번째 배열부터 0 ~ n번째 까지 순회하고 1번째 배열 순으로 계속해서 순회하며 말을 놓고 충돌을 확인하고, 충돌의 경우에 따라 배치 혹은 배치 취소의 작업을 연속 진행한다.
5. n개의 룩/퀸 배치가 완료된 체스판 경우의 수를 모아서 리턴하는 것이 최종 목표이다.

주어진 시간 내에 count N Rooks Solution부터 풀질 못했다...ㅜㅜ
나중을 위해 의사코드라도 남겨본다...

• findNRooksSolution: n * n 개의 체스판에 n개의 룩이 배치되는 다양한 케이스 중 1개 체스판 반환 -> (0,0), (1,1), (2,2), (3,3) ... (n,n) 식으로 배치하도록 코드를 짰다.

window.findNRooksSolution = function(n) {
  var solution = new Board({ n: n });

  for (let i = 0; i < solution.attributes["n"]; i++) {
    solution.togglePiece(i, i);
  }
  console.log("Single solution for " + n + " rooks:", JSON.stringify(solution));
  return solution.rows();
};

• countNRooksSolution: n * n 개의 체스판에 n개의 룩이 배치되는 모든 경우의 수 반환

/* row : 0~4 , col: 0~4
  row: 0~4, col: 1~4
  row: 0~4. col: 2~4
  row:0~4, col: 3~4 -> 검사할 것이 없다. 재귀 끝(탈출 조건)
  재귀용 카운트 = 0
   for(row : ~ n까지)
    for(col: ~ n까지)
     토글 처리 먼저
      충돌검사
      	충돌이다 -> 토클처리 한번 더
        아니면 -> 재귀용 카운드 1 올리고, 기준을 바꿔서 재귀
     
  재귀가 다 끝나면
  재귀용 카운트가 n-1번 호출되면 인지 검사해서 솔루션 카운트를 1 올림
  재귀용 카운트는 0으로 초기화
  다시 row를 1올려서 다시 재귀*/

• findNQueensSolution: n * n 개의 체스판에 n개의 퀸이 배치되는 다양한 케이스 중 1개 체스판 반환
• countNQueensSolution: n * n 개의 체스판에 n개의 퀸이 배치되는 모든 경우의 수 반환

3. 새로운 개념: DFS와 Back Tracking

1. 의사코드나 머리 속으로 그림을 그리는 것이 꽤 오래 걸렸다. 그래서 결론적으로는 알고리즘 작성을 완료하지 못했다.
2. 대신 의사코드로 고민하는 과정에서 재귀를 이용한 DFS 방식과 Back Tracking이라는 개념을 좀 더 익혀 볼 수 있었다.

• DFS: Graph/Tree 구조에서 볼 수 있는 검색 방법으로, 노드 -> 하위 노드 -> 하위의 하위 노드 순으로 깊이 있게 탐색을 진행하는 경우이다. 루트 노드부터 시작하여 한 방향으로 리프 노드까지 검색을 하였으나 원하는 값을 찾지 못한다면 다시 루트로 올라와 그 다음 노드 방향으로 상에서 하 방향으로 검색을 진행하는 것이 특징이다.
  반대 개념으로는 BFS(같은 레벨의 노드들을 먼저 검색한 후 하위 레벨의 노드들을 검색하는 방법)이 있다. 검색 과정에서는 stack을 사용한다.
  참고 링크: https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html
  N-Rooks나 N-Queens에서 행 기준으로 말을 올려둔 체스판이 노드로 있고, 그 하위에 다음 행에 말이 추가로 배치된 체스판들이 노드로 있다고 생각한다면 충돌이 없는 케이스들을 찾기 위해 DFS를 실행할 수 있다.
• Back Tracking: 어떠한 조건이 합치하는 모든 경우의 수를 내고자 할 때 사용하는 방식이다. N-Queens의 경우에는 퀸이라는 말이 가지는 조건(행, 열, 양 대각선에 말이 있으면 안됨)이 어겨지지 않는 상황에서 n개의 퀸을 체스판에 배치하는 모든 경우의 수를 내려고 하기에 back tracking이 적용된다.
  예를 들어, 2번째 행까지 2개의 퀸을 배치하는데 성공하였다 하여도 앞선 2개의 퀸의 규칙으로 인해 3, 4번째 행에 퀸을 둘 자리가 없다면 이 경우는 '유망성이 없는 검색'으로 취급하여 2번째 행으로 돌아와 다른 자리로 말을 옮겨 경우의 수를 따진다.
  유망성이 있느냐 없느냐를 기준으로 검색을 보류하거나 진행할 수 있기 때문에 일반적인 DFS 보다 효율적으로 문제를 해결할 수 있는 방법이다.

이미지 출처: https://daisyleetcode2014.wordpress.com/2014/05/12/n-queens%E8%A7%A3%E6%B3%95-dfs/