PriorityQueue (우선순위큐)
FIFO를 따르는 Queue와는 달리
- 우선순위큐는 들어간 순서에 상관 없이 우선순위가 높은 데이터가 먼저 나온다는 특징을 갖고 있다.
- 우선순위큐는 힙(Heap)이라는 자료구조로 구현한다.
Implementation of Priority Queue (우선순위큐의 구현)
- An array
- LinkedList
- a heap data structure
배열, 연결리스트, 힙을 이용해서 구현할 수 있다. 일반적으로 힙(Heap)을 사용한다.
Why don't we use arrays or linked lists when implementing a priority queue? (우선순위큐를 구현할 때 배열, 연결리스트를 사용하지 않는 이유?)
Array (배열)
- 우선순위가 높은대로 배열의 가장 앞 부분부터 넣는다면, 우선순위가 높은대로 배열 맨 앞의 인덱스를 이용하면 된다.
- 하지만, 삽입 과정에서 우선순위가 중간인 것이 들어가야 한다면?
- 배열 특성 상, 삽입과 삭제 과정에서 데이터를 한 칸씩 뒤로 밀거나 앞으로 당겨야 하기 때문에 비효율적이다.
- 최악의 경우, 삽입 위치를 찾기 위해 배열의 모든 인덱스를 탐색해야 할 수도 있다.
- 이 때 시간 복잡도는 자료가 n개라고 할 때 O(n)이 된다. → 배열로 구현 시 시간 복잡도 삭제는
O(1), 삽입은O(n)
- 이 때 시간 복잡도는 자료가 n개라고 할 때 O(n)이 된다. → 배열로 구현 시 시간 복잡도 삭제는
LinkedList (연결리스트)
- 연결 리스트의 장점을 생각해보자. 삽입과 삭제 과정에서 한 칸씩 밀거나 당기는 연산이 불필요하다는 점이다. (노드를 통해 인접한 노드끼리 참조 형태로 저장되어 있기 때문에)
- 연결리스트로 우선순위큐를 구현할 경우, 우선순위가 높은 순서대로 연결시키면 우선순위가 높은 데이터의 반환은 배열과 동일하게 쉽다.
- 하지만, 연결리스트 또한 배열과 마찬가지로 삽입과 삭제 과정에서 그 위치를 찾아야 한다.
- 최악의 경우, 삽입 위치를 찾기 위해 맨 끝까지 가게된다. → 연결리스트로 구현 시 시간 복잡도: 삭제는
O(1), 삽입은O(n)
Heap(힙)
- 힙의 경우 삭제, 삽입 과정에서 부모, 자식 노드 간의 비교로만 계속 이뤄진다.
- 즉, 이진 트리의 높이가 하나 증가할 때마다 저장 가능한 자료 개수는 2배 증가하고, 비교 연산 횟수는 1회 증가한다. → 시간 복잡도: 삭제는
O(log2n), 삽입은O(log2n)
배열, 연결 리스트가 삭제에서는 시간 복잡도의 우위를 점할지라도 삽입의 시간 복잡도가 힙 기반이 훨씬 월등하기에 힙으로 구현하는 것이다.
힙(Heap)
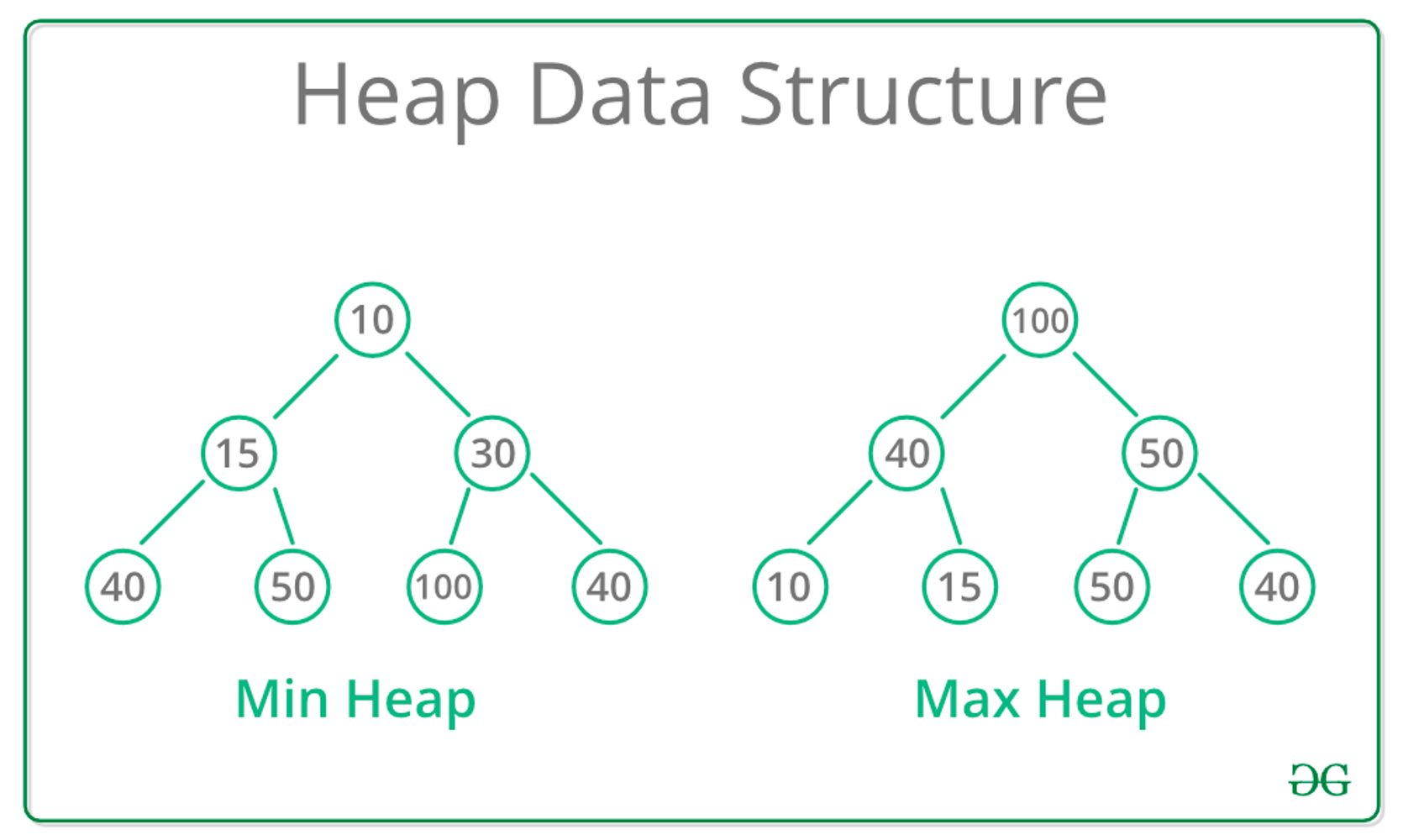
힙이란 이진트리이되 완전 이진트리이고, 모든 노드에 저장된 값은 자식 노드에 저장된 값보다 크거나 작아야 하는 자료구조이다.
Max Heap(최대 힙):루트노드의 값이 가장 큰 경우Min Heap(최소 힙):루트노드의 값이 가장 작은 경우
→ 즉, 힙은 루트노드에 우선순위가 가장 높은 데이터를 위치시킬 수 있기 때문에 우선순위큐를 구현할 수 있는 자료구조이다.
왜? 힙에 저장된 노드를 뺄 때마다 우선순위가 높은 데이터가 먼저 빠져나오기 때문이다.
Max Heap(최대 힙)
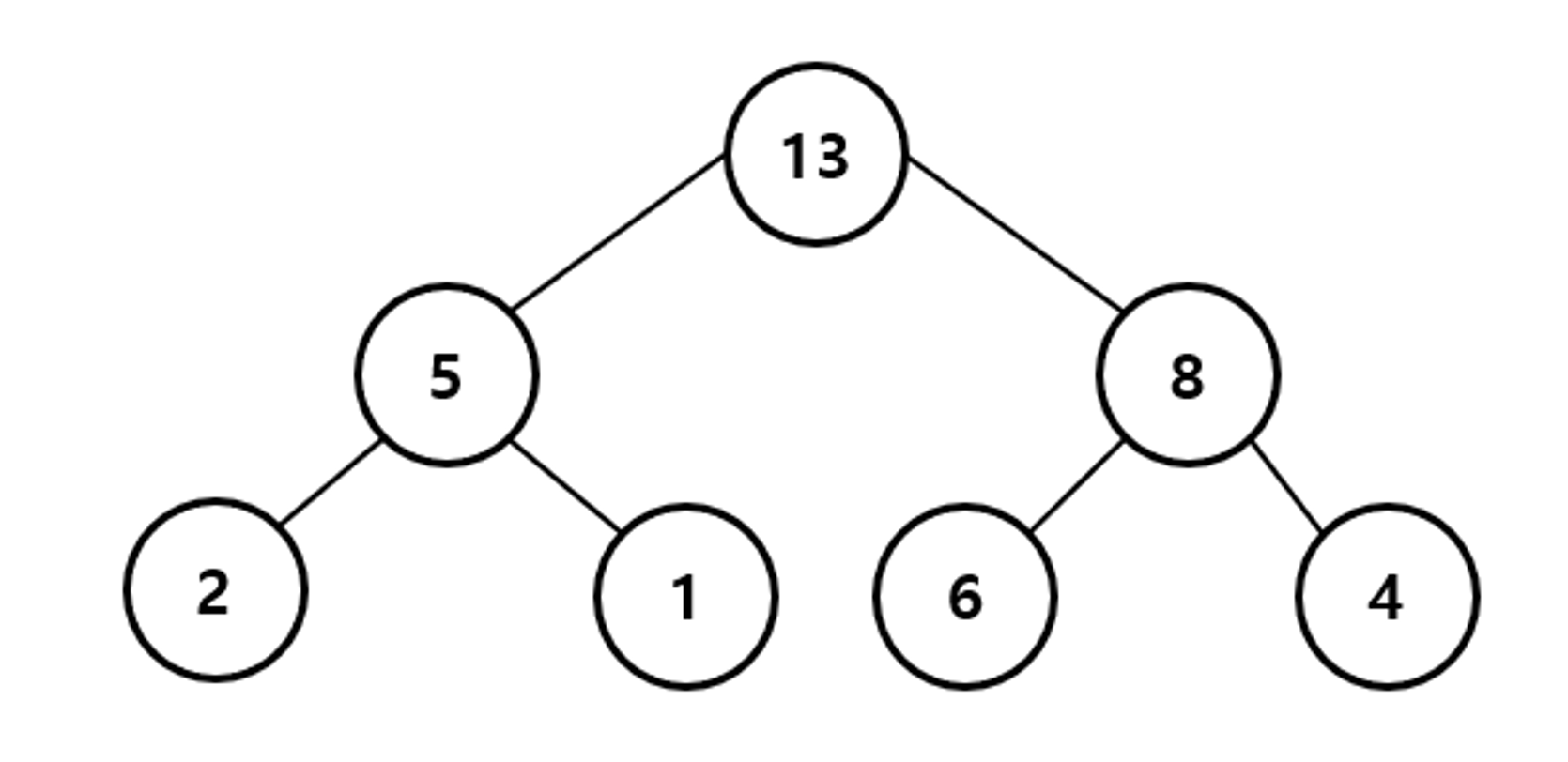
최대힙은
- 완전 이진트리이면서, 루트노드로 올라갈 수록 저장된 값이 커지는 구조이다. (=루트 노드의 값이 가장 큰 경우)
- 우선 순위는 값이 큰 순서대로 매긴다.
Min Heap(최소 힙)
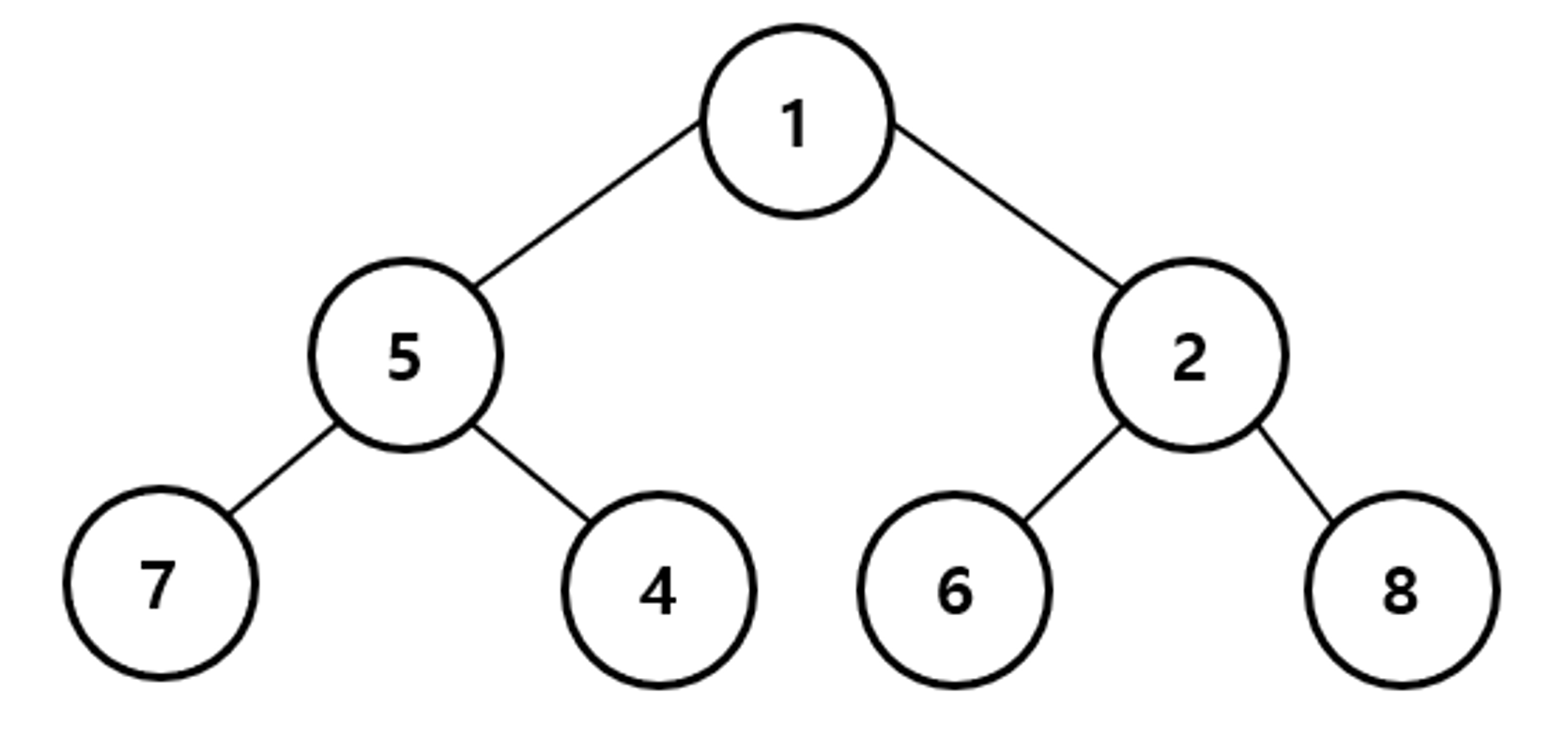
최소힙은
- 완전 이진트리이면서, 루트노드로 올라갈 수록 저장된 값이 작아지는 구조이다. (=루트 노드의 값이 가장 작은 경우)
- 우선 순위는 값이 작은 순서대로 매긴다.
최대 힙이든, 최소 힙이든 루트노드에는 가장 우선순위가 높은 것이 자리잡게 된다.
힙(Heap)에서의 데이터 저장 과정
최소힙에 저장할 때
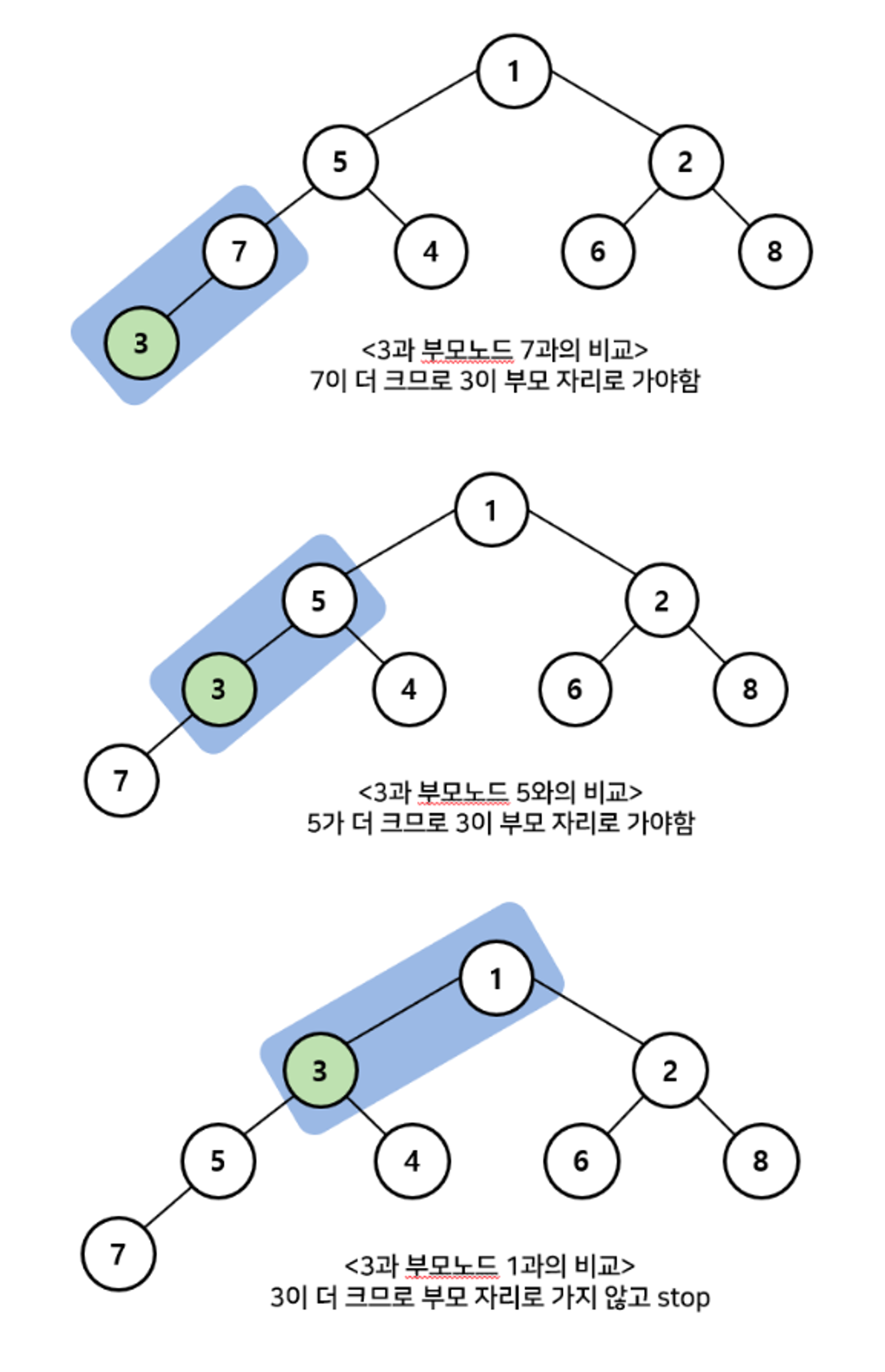
최대힙은 반대로 부모와 비교해 자식이 크면 서로 자리를 바꿔주면 된다. 여기서, 힙(Heap)은 배열로 구현하는 것이 적합하다.
왜? 힙은
배열로 구현하는 것이 적합한가? 우선순위큐는 힙으로 구현하는데, 왜 갑자기배열?
힙은 완전 이진트리의 형태를 띄기 때문에 → 위에서부터 아래로, 왼쪽에서 부터 오른쪽으로 노드가 차곡차곡 채워지는 형태로 (= 중간에 빈 공간이 없다.) 이 점이 배열의 인덱스와 잘 매칭되기 때문이다. 그래서 힙의 노드를 배열의 요소에 순차적으로 배치할 수 있기 때문이다.
또한, 배열을 사용하면 부모 노드와 자식 노드간의 관계를 배열 인덱스를 통해 쉽게 파악하고 연산할 수 있다. (아래에서 다시 복기하기)
힙 구현
-
완전이진트리
힙은 배열로 구현하는 것이 가장 효율적이다. 루트부터 시작해서 위 → 아래로, 왼쪽 →오른쪽으로 진행 공간 없이 차곡차곡 노드를 쌓는다.
트리를 순회하면서 인덱스를 부여한다. 즉, 루트 노드는 배열 인덱스 0값을 갖는다.
-
트리의 부모 ↔ 자식 관계
배열의 인덱스 연산으로 바뀐다.
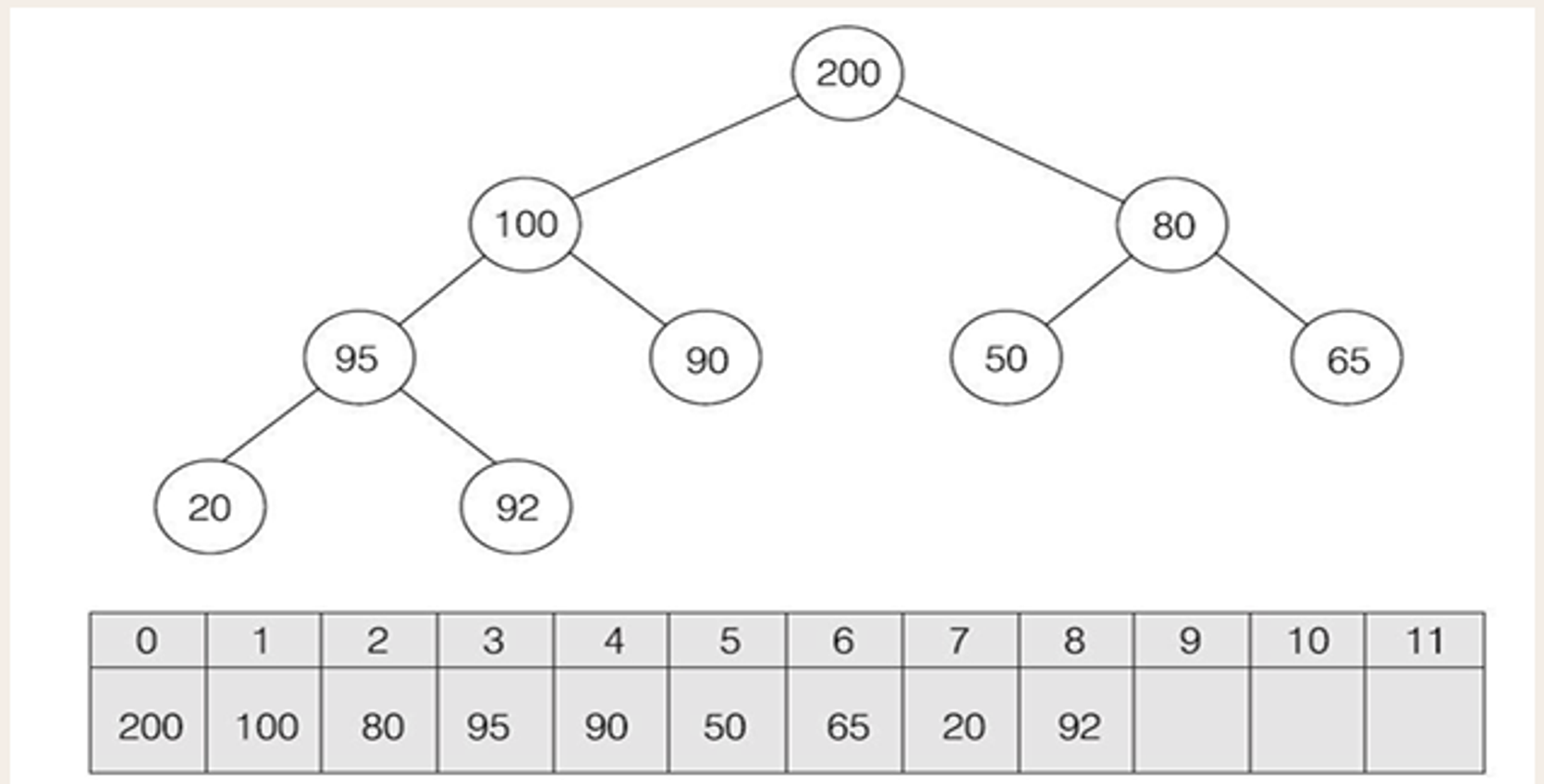
완전이진트리와 배열
- 루트노드 (200)은 배열 인덱스 0값을 갖는다.
- 왼쪽에서 → 오른쪽으로 진행된다.
- 인덱스 K에 있는 노드의 왼쪽 자식은 (2k+1)에
- 인덱스 K에 있는 노드의 오른쪽 자식은 (2k+2)에
- 인덱스 K에 있는 노드의 부모 노드는 (k-1) /2에
부모자식간의 관계, 배열의 인덱스 연산 짚고 넘어가기. 🫨
- 왼쪽 자식노드는 부모노드의 인덱스에 (2k+1)에 위치해있다.
- 힙의 완전 이진트리 특성 상, 부모 노드 하나 당, 자식 노드가 최대
2개 있기 때문이다. - 그럼 오른쪽 자식 노드는 +2를 해주면 된다. ⇒ 루트부터 시작해서 위에서 아래로, 왼쪽에서 오른쪽으로 진행되기 때문에.
- 인덱스 K에 있는 노드의 부모노드는 자식 노드의 인덱스에서 (k-1) / 2에 위치해있다.
- 부모노드는 자식 노드를 최대
2개 가질 수 있음을 정리했고, 나눠준다음 -1 (=1개인 부모노드, 2개 자식 노드의 배열 바로 앞 인덱스번지) 해주면 부모노드의 인덱스 값을 구할 수 있는 것이다.
- 부모노드는 자식 노드를 최대
힙(Heap) 의 데이터 삭제
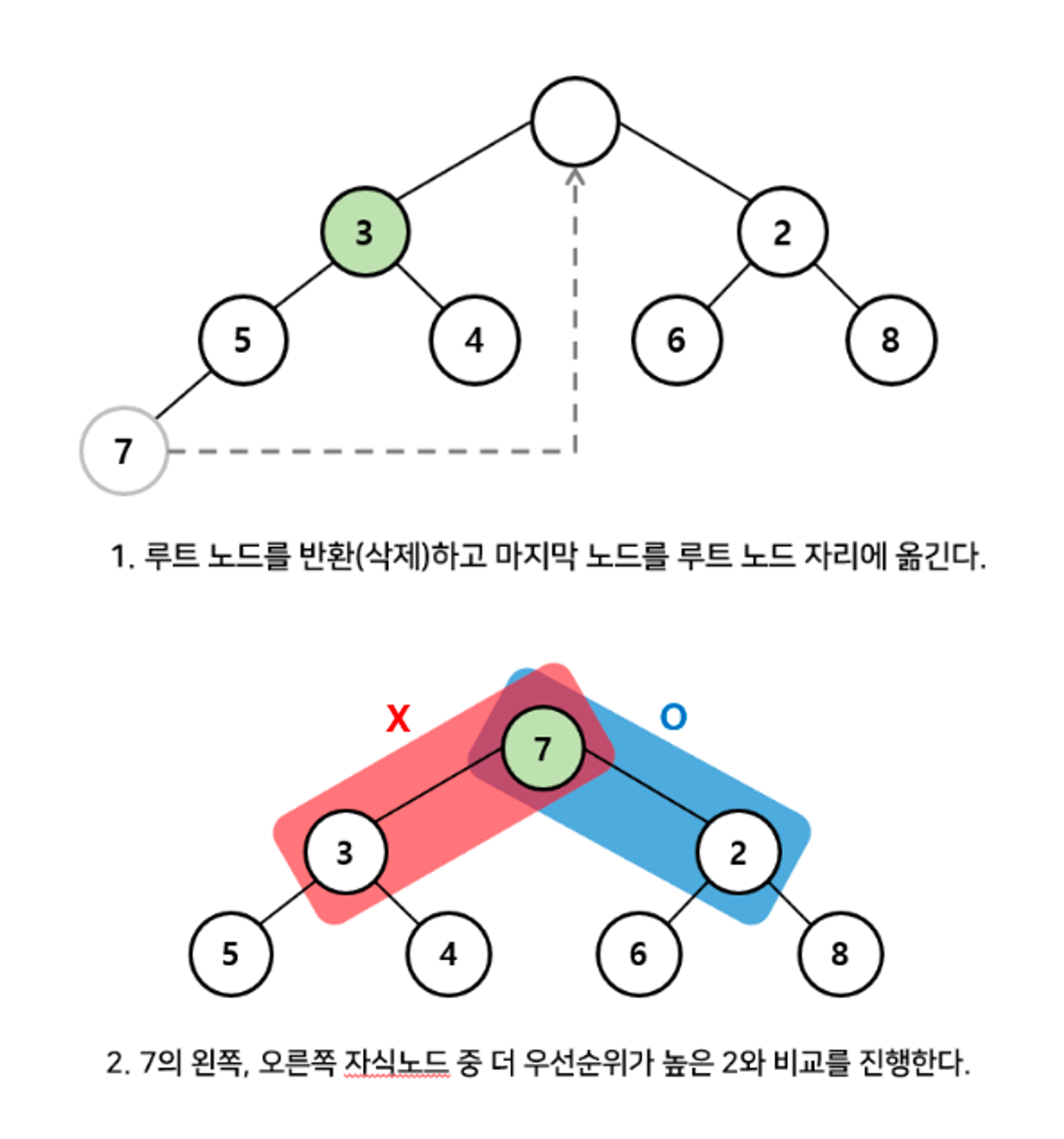
최소 힙에서 삭제할 때
우선순위 큐의 구현을 가정해보자. 우선순위 큐에서 pop 은 가장 우선순위가 높은 데이터를 빼낸다는 의미이다. = 힙의 루트 노드를 반환(삭제) 하는 것이다.
힙에서 가장 우선순위가 높은 데이터는 루트노드인데, 이 루트 노드를 삭제하면서 힙의 구조를 그대로 유지하는 것이 관건이다. (이 힙의 구조를 유지하는 과정을 heapify라고 한다.