Dynamic Programming (동적 계획법 - 4)

8. 연속하는 수들의 최대 합 구하기
9. 그리드(Grid)에서 경로 찾기
10. LCS(Longest common subsequence) 문제

8. 연속하는 수들의 최대 합 구하기

• 문제 : n개의 수 x0, x1, ..., x(n-1)에 대하여, 연속하는 수들의 최대 합을 구하라. (배열 num에 n개의 수들이 저장되어 있다.)

(1) 비효율적 방법 - 1

maxSum = -∞
for i = 0 to n-1
   for j = i to n-1
      // sum = num[i]부터 num[j]까지의 합
      sum = 0
      for k = i to j
         sum += num[k]
      if(maxSum < sum)
         maxSum = sum

• 시간 복잡도 : O(n^3)

(2) 비효율적 방법 -2

maxSum = -∞
for i = 0 to n-1
   sum = 0
   for j = i to n-1
      sum = sum + num[j]
      if (maxSum < sum)
         maxSum = sum

• 시간 복잡도 : O(n^2)

(3) 분할과 정복 알고리즘

• mid : 가운데 원소의 위치
• 배열의 원소들을 처음부터 mid까지의 수들과, mid+1부터 마지막까지의 수들로 나눈다.
• 왼쪽 절반의 (최적)해를 구한다. 이 해는 S1이라고 한다.
• 오른쪽 절반의 (최적)해를 구한다. 이 해는 S2라고 한다.
• 중간에 걸쳐있는 경우(mid의 좌우로 연속하는 수들)의 (최적)해를 구한다. 이 해를 S3라 한다.
• S1, S2, S3 중 좋은 해가 주어진 입력에 대한 (최적)해이다.

(4) 효율적 방법 - 동적 계획법

• 1) 부분문제 : x0, x1, ..., xi에 대하여 xi에서 끝나는 연속하는 수들의 최대 합을 구하라. (재귀적인 해를 고안)

• 2) 부분문제 (최적)해의 목적함수 :

  • sum[i] = x0, x1, ..., xi에 대하여 xi에서 끝나는 연속하는 수들의 최대 합
  • sum[i-1] = x0, x1, ..., x(i-1) (xi를 포함하는게 좋을지를 판단 - 양수면 포함, 음수면 불포함)

• 3) 주어진 문제의 (최적)해의 목적함수 : max{sum[i]} (0≤i≤n-1)

• 4) 부분문제 (최적)해의 목적함수에 대한 점화식(재귀식) (recurrence relation)

  • sum[i] = sum[i-1] + num[i] (if sum[i-1] ≥ 0)
  • sum[i] = num[i] (if sum[i-1] < 0)

• p[i] : x0, x1, ..., xi에 대하여 xi에서 끝나면서 합이 최대가 되는 연속하는 수들의 시작 위치

• p[i] = p[i-1] (if sum[i-1] ≥ 0)

• p[i] = i (otherwise)

//sum, num, p는 배열(리스트)
//sum은 합, num은 수, p는 시작 위치
sum[0] = num[0]
p[0] = 0
for i = 1 to n-1
   if (sum[i-1] ≥ 0)
      sum[i] = sum[i-1] + num[i]
      p[i] = p[i-1]
   else
      sum[i] = num[i]
      p[i] = i
      
return max(sum) // sum의 원소 중 최댓값 반환

-python code

def searchLinear(n):
    sum = [0 for i in range(n)]
    num = [4, -5, 7, -3, 6, -2, 9, -2, 4, -3, -2, 2, -3, -1, 2, 4]
    p = [0 for i in range(n)]

    for i in range(1, n):
        if (sum[i-1] >= 0):
            sum[i] = sum[i-1] + num[i]
            p[i] = p[i-1]
        else:
            sum[i] = num[i]
            p[i] = i
        
    print(p)
    print(sum)    
    return max(sum)

print(searchLinear(16))

• 시간 복잡도 : O(n)

9. 그리드(Grid)에서 경로 찾기

• 행 : 가로 줄, 열: 세로 줄

• The input is an n(행) x m(열) grid, in which each cell has a positive cost C(i,j) associated with it.

• The bottom row is row 1, the top row is row n.

• From a cell (i,j) in one step you can reach cells

  • (i+1, j-1) (if j > 1)
  • (i+1, j), (i+1, j+1) (if j < m)

• The goal is to find the least cost path from the bottom of the grid to the top, where the cost of a path is the sum of costs of cells used on that path. (지나는 셀들의 비용이 최소가 되는 경우 찾기)

• Example 4 x 5 Grid
  

---

• 부분문제(subproblem) 정의
  • bottom에서 셀(i,j)까지 가는 최소 비용의 경로를 찾아라.
• 부분문제의 최적 해 값(목적함수)
  • A(i,j) : bottom으로부터 셀 (i,j)에 가는 경로의 최소 비용
• 주어진 문제의 최적 해 값(목적함수)
  • min(A(n,j)) (1≤j≤m)
• 부분문제 최적 해 값(목적함수)의 재귀적 정의
  • A(i,j) = C(i, j) + min{A(i-1, j-1), A(i-1, j)} (if 1≤i≤n, j = m)
  • A(i, j) = C(i, j) + min{A(i-1, j), A(i-1, j+1)} (if 1≤i≤n, j = 1)
  • A(i, j) = C(i, j) + min{A(i-1, j-1), A(i-1, j), A(i-1, j+1)} (if 1≤i≤n, j ≠ 1 and j ≠ m)

Base case

• A(0, j) = 0 (for 1 ≤ j ≤ m) (i의 index가 0이면 값도 다 0)
• or A(1, j) = C(1,j) (for 1 ≤ j ≤ m) (i의 index가 1이면 해당 셀의 비용이 그대로 값이 됨)

# matrix= [[0 for i in range(m)] for j in range(n)]
import copy
m, n = map(int, input().split())
C = []
for i in range(m):
    C.append(list(map(int, input().split())))

print(C)

def grid(m, n, C):
    A = [0 for i in range(n)]
    for i in range(m-1, -1, -1):
        temp = copy.deepcopy(A) # 꼭 deepcopy 해주기! 
        # 아래서 temp 값 변경될 때 A도 같은 주소 참조 중이라
        # temp 변경시 함께 변경 될 수 있음!!
        for j in range(n):
            if j == 0 and j < n-1:
                temp[j] = C[i][j] + min(A[j], A[j+1])
            elif j == n-1:
                temp[j] = C[i][j] + min(A[j-1], A[j])
            else:
                temp[j] = C[i][j] + min(A[j-1], A[j], A[j+1])
        print("pre:", temp)                
        A = temp
        # print("after:",A)
    return min(A)

print(grid(m, n, C))

# 4 5
# 2 8 9 5 8
# 4 4 6 2 3
# 5 7 5 6 1
# 3 2 5 4 8

시간복잡도 : O(mn)

예시 그림 :

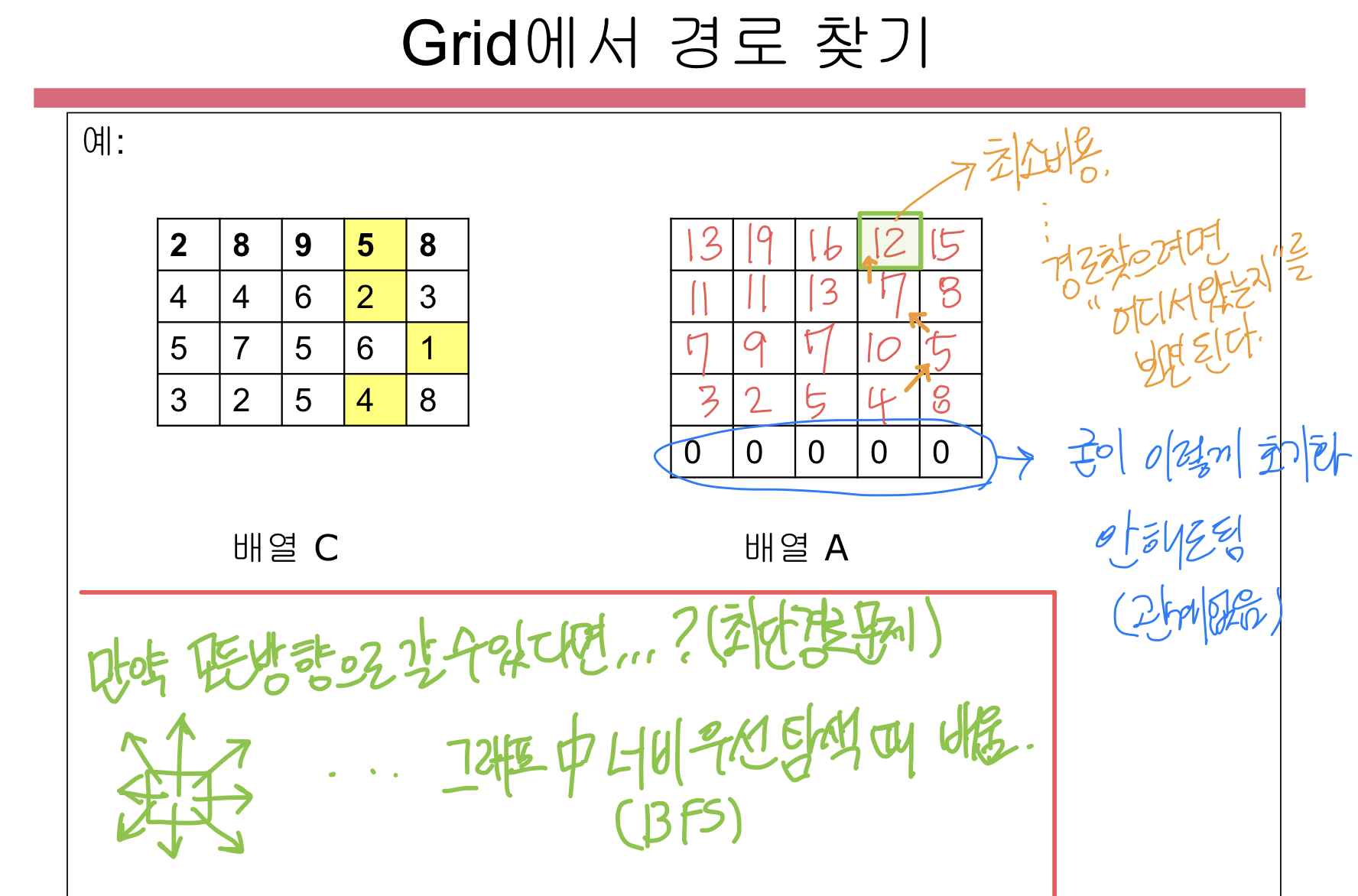
10. LCS(Longest Common Subsequence) 문제

• 문자열 X = ABCBDAB

• X의 부분 수열(or 서열) (subsequence)은 X에서 몇 개의 문자를 지워서 얻어진다.

• ex :

  • ABD, ABBB, BBDA는 부분서열이다.
  • AABB는 부분서열이 아니다.

• LCS problem

  • 입력으로 주어진 두 문자열 X, Y에서 공통된 가장 긴 부분서열을 찾아라.
  • X = x1x2x3...xn, Y = y1y2y3...ym
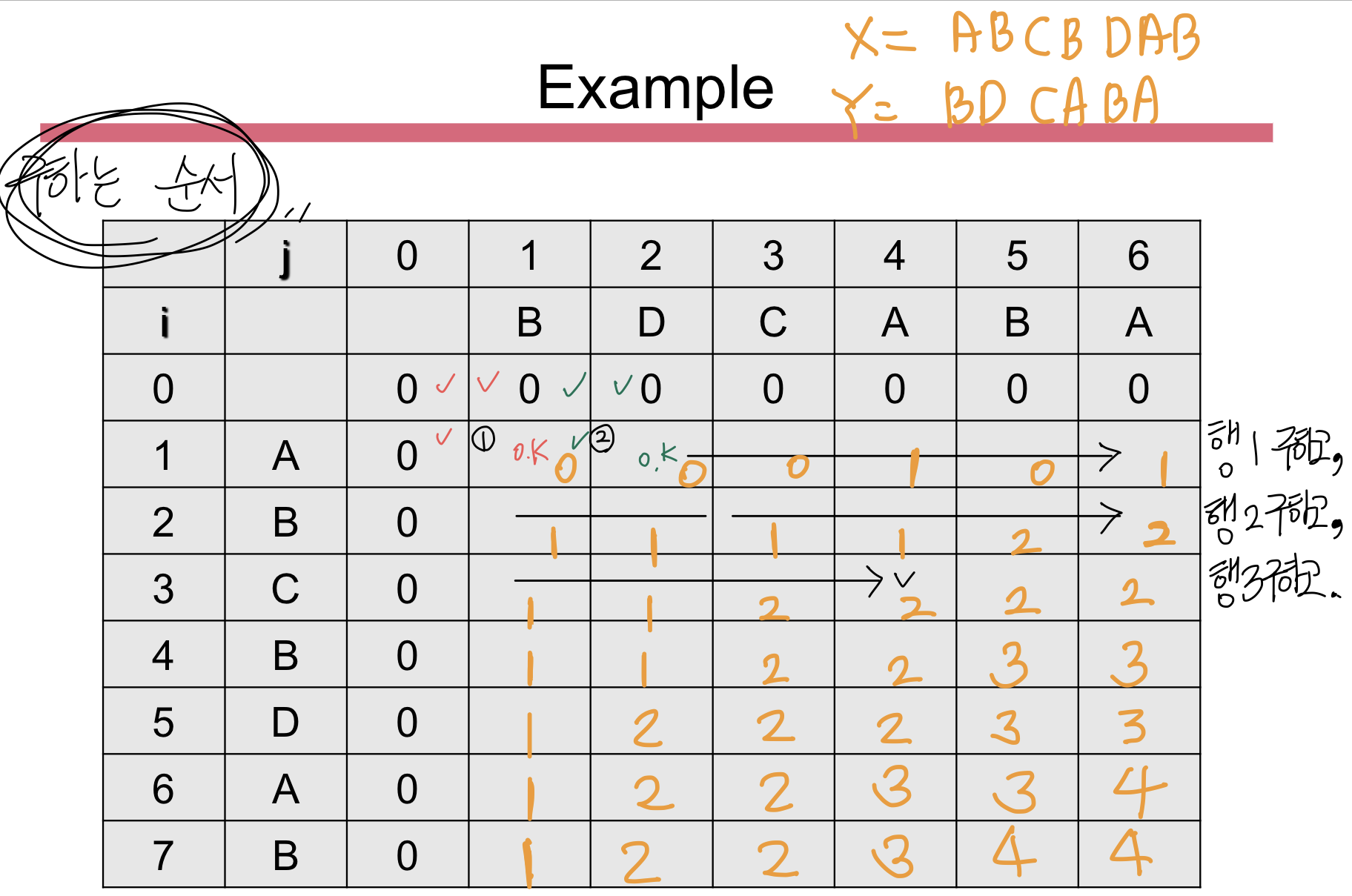
  • 만약, X = ABCBDAB, Y = BDCAB라면 BCA는 부분서열이지만, LCS는 아니다.
  • LCS ? BDAB, BCAB

• 두 개의 DNA 순서열(sequence)이 있을 때, 이 두 개가 얼마나 비슷한가를 자주 측정하는 일이 발생된다.

• 예를 들어 아래와 같이 X, Y가 존재한다면,

  • X = ACCGGTCGAAGCCGGCCAA
  • Y = TTTCCCACTCGTGTCGACGTGTAAGCCTTAAGGCCAA

• 이 때 둘은 얼마나 유사한가를 측정할 때, 둘의 LCS(순서가 유지)를 구하여 이것이 길면 길수록 둘은 더 유사한 것이 된다. (두 문자열의 유사도 측정의 의미)

---

• Subsequence(부분서열) 문제 (쉬움)
  • X = x1x2x3...xn, Y = y1y2y3...ym의 Subsequence(부분서열)을 구하라.
  • 단순한 방법 : X의 모든 부분서열에 대하여 이것이 Y의 부분서열인지 조사
    • X의 부분서열의 개수는 2^n개 이므로 이 방법은 Ω(2^n)의 시간이 걸린다.

---

• LCS 문제
  • X(= x1x2x3...xn)가 Y(= y1y2y3...ym)의 LCS인가?

i = j = 1
while (i ≤ n and j ≤ m)
   if(xi == yj)
      i += 1 (X의 위치 이동)
      j += 1 (Y의 위치 이동)
   else
      j += 1 (xi ≠ yj) (Y의 위치만 이동)
if (i > n)
   X is a subsequence of Y (X는 Y의 부분서열이다.)
else
   X is not a subsequence of Y (X는 Y의 부분서열이 아니다.)

수행시간 : O(n + m)

---

• 부분문제 (subproblem) 정의 : Xi와 Yj의 LCS를 구하라.
• 부분문제의 최적 해 값(목적함수) :
  • L(i, j) : Xi와 Yj의 LCS의 길이
• 주어진 문제의 최적 해 값(목적함수) : L(n,m)
• 부분문제 최적 해 값(목적함수)의 재귀적 정의
  • L(i, j) = 0 (if i = 0 or j = 0)
  • L(i, j) = L(i-1, j-1) + 1 (if xi = yj)
  • L(i, j) = max{L(i, j-1), L(i-1, j)} (if xi ≠ yj)
    (xi, yj 둘 중 하나가 들어가지 않는 LCS를 구하면 된다.)
    (길이만 구하려면 굳이 2차원 테이블이 필요하지 않다.
    ~ 한 줄만 있어도 됨(그 직전 줄 구하면 직전의 직전줄은 없어도 된다는 말))
    (Y가 X보다 작을 때 or X가 Y보다 작을 때)

# import copy
x = "%"+input()
y = "%"+input()

print(x, y)
print(len(x), len(y))

def LCS(x, y):
    C = [[0 for i in range(len(y))] for j in range(len(x))]
    L = [0 for i in range(len(y))]
    for i in range(len(x)):
        # temp = copy.deepcopy(L)
        for j in range(len(y)):
            if i == 0 or j == 0:
                C[i][j] = 0
            elif x[i] == y[j]:
                C[i][j] = C[i-1][j-1] + 1
            else:
                C[i][j] = max(C[i][j-1], C[i-1][j])
    print(C)
    return C[len(x)-1][len(y)-1] 
                


print(LCS(x, y))
  %  B  D  C  A  B  A
[[0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 1, 1, 1], 
 [0, 1, 1, 1, 1, 2, 2], 
 [0, 1, 1, 2, 2, 2, 2], 
 [0, 1, 1, 2, 2, 3, 3], 
 [0, 1, 2, 2, 2, 3, 3], 
 [0, 1, 2, 2, 3, 3, 4], 
 [0, 1, 2, 2, 3, 4, 4]]

# ABCBDAB
# BDCABA