Dynamic Programming (동적 계획법 - 5)
- Assembly line scheduling
11. Assembly line scheduling
1. 개념 설명
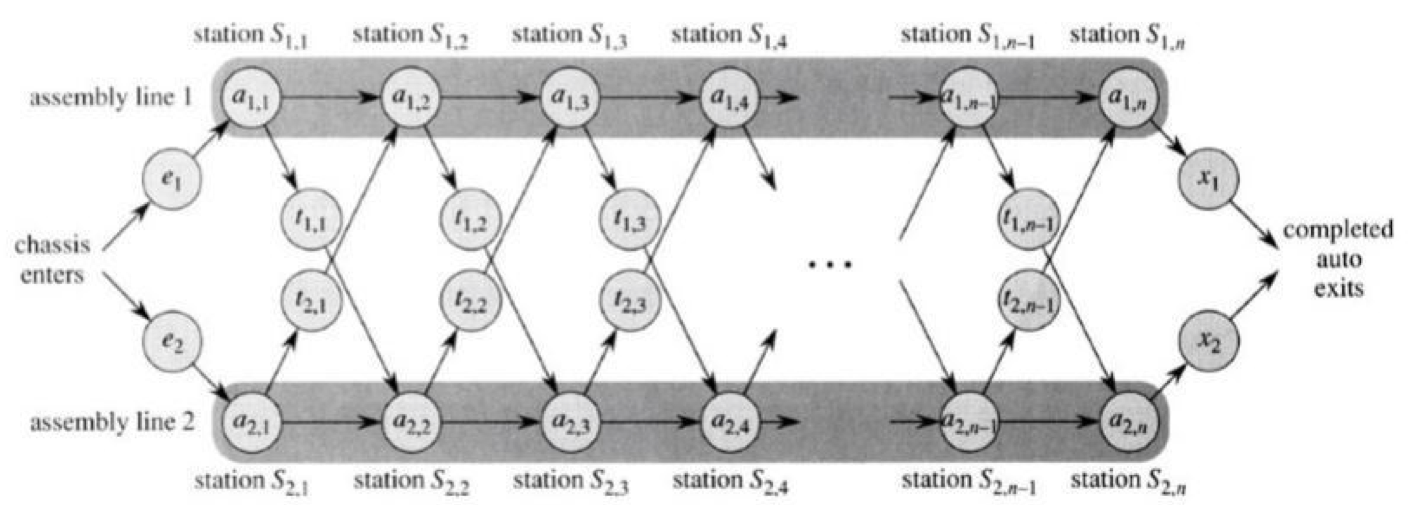
- Car chassis를 조립하기 위한 특정 공장에 두 개의 라인이 있다고 가정하자.
- 그림에서 위의 라인이 1, 아래의 라인이 2이다.
- 각 라인에서 진행되는 1부터 n까지의 조립공정(station에서 수행)이 있다.
- 같은 열에 있는 공정은 같은 공정이지만 라인에 따른 시간차이가 있다.
- 위 또는 아래의 라인에서 다른 라인으로 넘어 가려면 시간이 소요된다. 같은 라인에서 넘어가는 시간은 0이라고 가정한다.
- 문제 : Car chassis를 완성하는데 걸리는 최소 시간을 구하라.
우선 각 기호에 대한 개념은 아래와 같다.
- Si,j : i라인에서의 j번째 공정(j-th station on line i)
- ai,j : Si,j에서 공정에 소요되는 시간(Assembly time required at station Si,j)
- ei : i 라인으로 들어가는 데 소요되는 시간(time to enter line i)
- xi : i 라인에서 나오는 데 소요되는 시간(time to exit line i)
- ti,j : j번째 공정을 하고 i라인에서 다른 라인으로 교체되는 시간(time to transfer from line i after station j)
참고 : Tigercow.Door
예시)
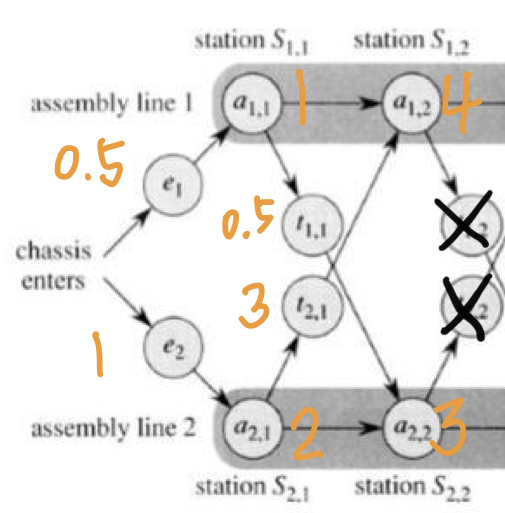
위와 같이 각 단계 별로 주황색 글씨의 시간이 주어졌다고 가정한다.
이 때, 두 번째 공정까지 진행하는 최단 시간과 그 과정을 알아보자.
(이러한 문제를 해결하는 것이 Assembly Line Scheduling)
- 첫 번째 공정을 마무리하는 시점
- S1,1 = e1 + a1,1 = 1.5s
- S2,1 = e2 + a2,1 = 3s
- 두 번째 공정을 마무리하는 시점
- S1,1 -> S1,2
- e1 + a1,1 + a1,2 = 5.5s
- S2,1 -> S1,2
- e2 + a2,1 + t2,1 + a1,2 = 10s
- S1,1 -> S2,2
- e1 + a1,1 + t1,1 + a2,2 = 5s (최단 시간)
- S2,1 -> S2,2
- e2 + a2,1 + a2,2 = 6s
- S1,1 -> S1,2
2. Brute-force
-
최적의 답을 찾기 위해 전체 경우의 수를 고려하면, n개의 공정이 있다고 가정할 때, 2개의 라인이 존재하므로 2^n개의 경우의 수를 고려해야 한다.
-
S1,n의 공정을 수행하는 데 오는 경로는 S1,(n-1)과 S2,(n-1)이 있으므로, 특정 위치의 공정을 위한 경로를 확인하면, 각각 2개씩 존재함을 알 수 있고, 공정은 총 n개이기 때문에 2^n개를 확인해야하는 것이다.
-
즉, 이러한 모든 경우의 수를 탐색하는 Brute-force Approach로는 다음과 같은 시간 복잡도를 가진다.
- T(n) = Ω(2^n)
-
동적 프로그래밍을 통해 해당 Assembly Line Scheduling 문제를 선형시간 안에 탐색할 수 있다. 아래에서 동적 프로그래밍을 통한 알고리즘 구현을 살펴보자.
*참고* 스테이션도 많고, 시간도 임의로 주어질 때로 확장이 가능하다.
3. 동적 프로그래밍으로 ALS 해결
- 동적 프로그래밍의 기본 핵심은 "테이블" 사용
- 모든 경우의 수에 대한 탐색이 아닌 필요한 경우, 테이블에서 참조
fi[j] : 시작 위치에서부터 스테이션 Si,j까지 조립하는데 걸리는 최소 시간
f* : 조립을 완료하는 데 걸리는 최소 시간(최종적으로 가장 빠른 시간을 저장하는 변수)
2개의 라인이 있다고 가정할 때, f*는 다음과 같이 구한다.
f* = min(f1[n]+x1, f2[n]+x2)
(xi = i라인에서 나오는 데 소요되는 시간)
각 테이블을 구성하는 방법은 다음과 같다.
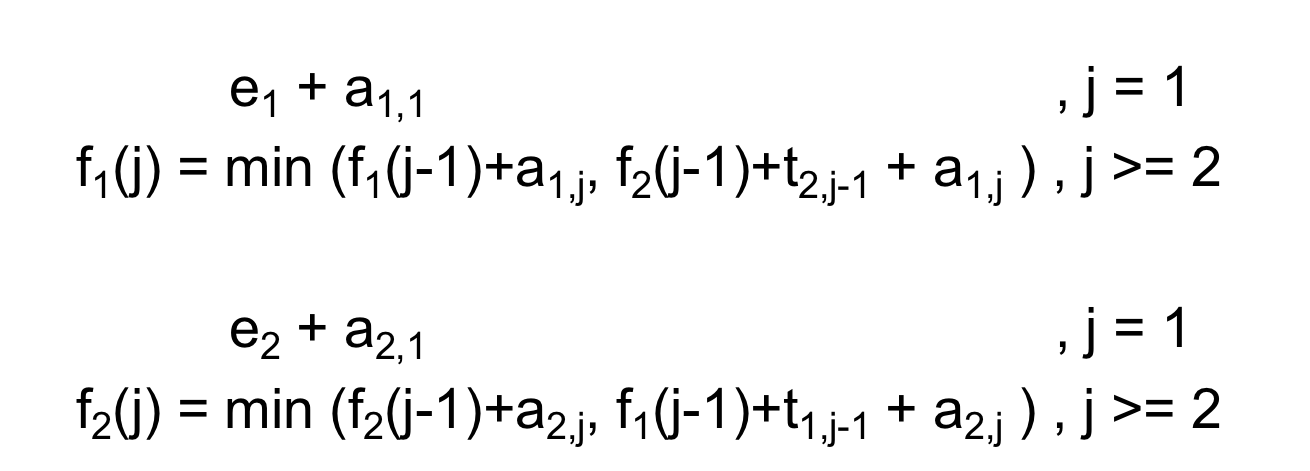
이를 통해 최종적으로 구성되는 (1)pseudo 코드와 (2)python 코드는 다음과 같다.
여기서 l1[j]는 S1,j에 오는 데에 어떠한 라인에서 오는 것이 최적인지를 구분하는 라인의 번호를 의미한다.
(1) Pseudo-code
Fastest-Way(a, t, e, x, n)
f1[1] <- e1+a1,1
f2[1] <- e2+a2,1
for j = 2 to n
do if f1[j-1] + a1,j ≤ f2[j-1] + t2,j-1 + a1,j
then f1[j] <- f1[j-1] + a1,j
l1[j] <- 1
else f1[j] <- f2[j-1] + t2,j-1 + a1,j
l1[j] <- 2
if f2[j-1] + a2,j ≤ f1[j-1] + t1,j-1 + a2,j
then f2[j] <- f1[j-1] + a1,j
l2[j] <- 2
else f2[j] <- f1[j-1] + t1,j-1 + a2,j
l2[j] <- 1
if f1[n] + x1 ≤ f2[n] + x2
then f* = f1[n] + x1
l* = 1
else f* = f2[n] + x2
l* = 2
(2) Python-code
def f(a, b, n, e1, e2, x1, x2, t1, t2):
f1 = [0 for x in range(n)]
f2 = [0 for x in range(n)]
f1[0] = e1 + a[0]
f2[0] = e2 + b[0]
for i in range(1, n):
f1[i] = min(f1[i-1], f2[i-1] + t2[i-1]) + a[i]
f2[i] = min(f2[i-1], f1[i-1] + t1[i-1]) + b[i]
# print(f1)
# print(f2)
return min(f1[n-1]+x1, f2[n-1]+x2)
(예시 사진 추가)
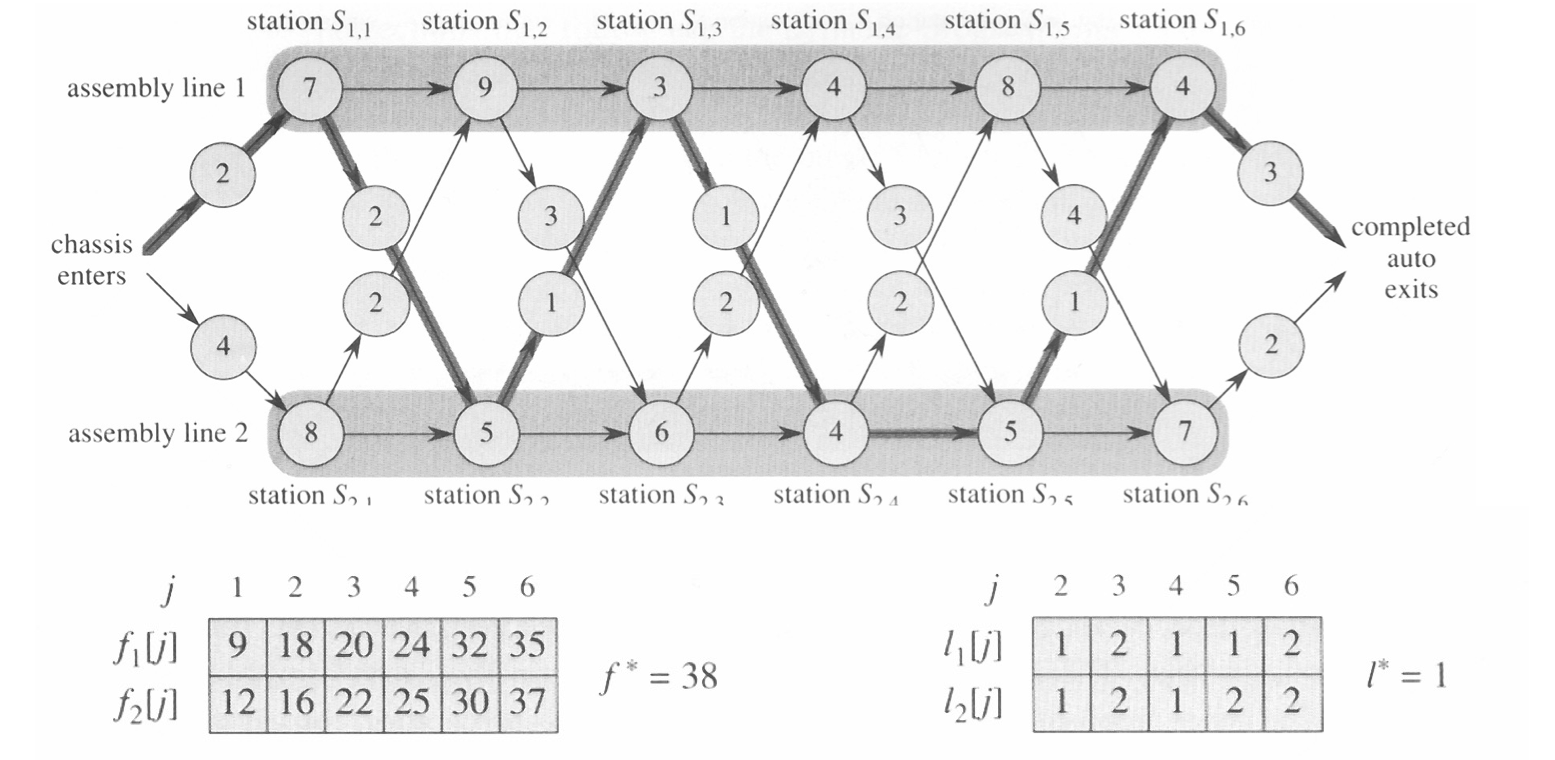

들렀다 갑니다 번창하세요 ^^