Graph (그래프)

• 그래프의 정의
• 용어 설명
• 그래프 표현

1. 그래프의 정의

• 그래프(Graph) 혹은 무향 그래프(undirected graph) G는 다음의 두 집합 V, E로 정의 된다. : G = (V, E)

  • V : 정점(Vertex)들의 집합 (정점 대신 노드를 사용하기도 함)
  • E : 에지(Edge, 간선)들의 집합 (정점들 사이의 관계를 나타냄)
    • E의 원소(에지 or 간선)는 정점들의 쌍 (v, w) (순서 고려 X)

• 방향 그래프(유향 그래프, directed graph or digraph) G는 두 집합 V, E로 정의 된다. : G = (V, E)

  • V : 정점들의 집합
  • E : 에지들의 집합
    • E의 원소(에지, 유향에지, 간선)는 정점들의 순서쌍 (v, w) (순서 고려)

• 그래프의 graphical representation

  • vertex u는 u🔘
  • (무향) 그래프의 에지 (u, v) : u🔘⎯⎯⎯⎯🔘v
  • 방향 그래프의 에지 (u, v) : u🔘⟶🔘v

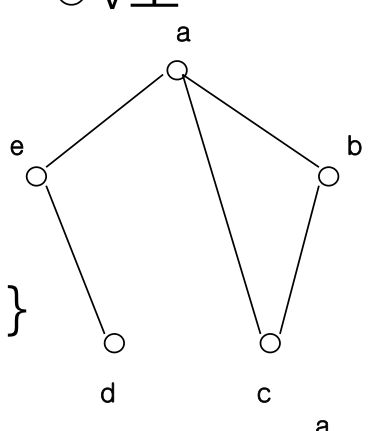
• ex. 그래프 G = (V, E)

  • V = {a, b, c, d, e}
  • E = {(a,b), (b,c), (d,e), (a,e), (a,c)}
    

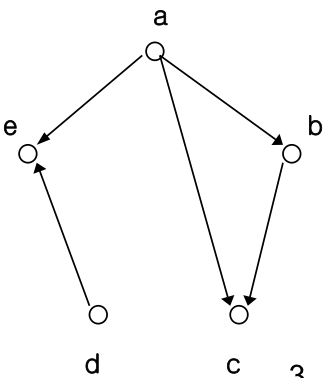
• ex. 방향그래프 G = (V, E)

  • V = {a, b, c, d, e}
  • E = {(a,b), (b,c), (d,e), (a,e), (a,c)}
    

---

• 쾨니히스베르크의 다리문제
  

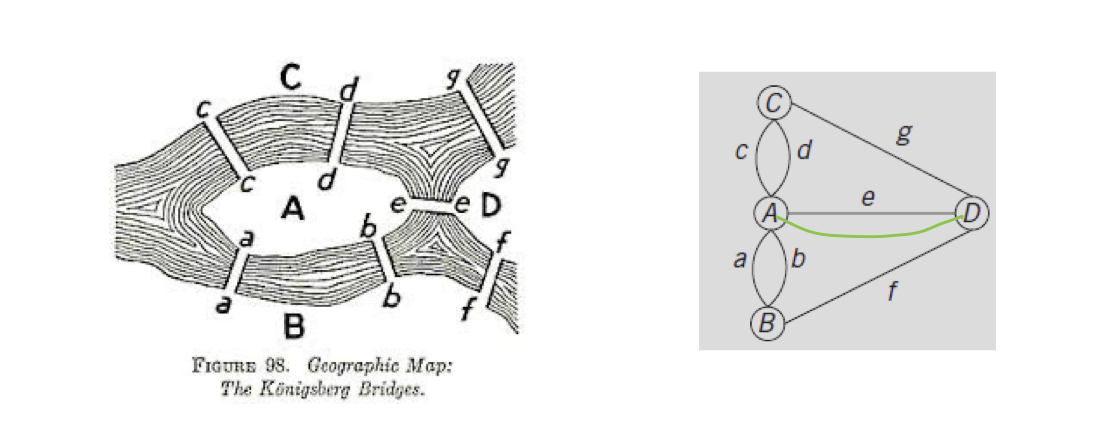
프로이센의 쾨니히스베르크에는 프로셀 강이 흐르는데, 이 강에는 안 쪽에 두 개의 큰 섬과 각 섬을 연결하는 총 7개의 다리가 있었다. 이 때 7개의 다리들을 한 번씩만 건너면서 처음 시작한 위치로 돌아오는 길이 존재하는가?

• 오일러(Euler)가 그러한 길이 존재하지 않음을 증명하였다. (한붓그리기 불가)
  • 오일러는 모든 정점이 짝수 개의 차수(Degree)를 갖는다면 모든 다리를 한 번씩만 건너서 도달하는 것이 성립한다고 말했다. (이 후 오일러의 정리..)
• 이 문제는 평면 그래프에서의 한붓그리기 문제로 그래프 이론의 시초이다.

• Euler Path : 꼭 시작 지점으로 돌아오지 않아도 됨
• Euler Cycle : 꼭 시작 지점으로 돌아와야 함

그래프 응용 분야

(1) 도로망

• 도시 : vertex
• 두 도시를 직접 연결하는 도로 : edge

(2) 컴퓨터 망

• 컴퓨터 : vertex
• 두 컴퓨터 사이의 통신 link : edge

(3) 웹 그래프 (Web Graph)

• web page : vertex
• hiperlink : edge

(4) Social Networks

• person : vertex
• relation : edge

그래프와 관련한 문제들

(실생활 여러 문제들을 그래프로 모델링하여 해결 가능)

• 도로망에서 도시 A로 갈 수 있는 모든 도시들 찾기
• 도시 A에서 도시 B까지 가장 빨리가는 경로
• 에지에 가중치를 둘 수도 있음
  • 지하철 두 역 사이를 지나는 데 걸리는 시간

---

2. 용어 설명

• 그래프 G = (V, E)의 부그래프(subgraph)

  • V' ⊆ V and E' ⊆ E 인 그래프 G' = (V', E')를 G의 부그래프라고 함.

• 완전 그래프(A complete graph) : 모든 두 정점 사이에 에지가 있는 그래프

• v와 w가 인접하다(v is adjacent to w) : 모든 두 정점 사이에 에지가 있는 그래프

• 에지 (v, w)는 정점 v, w에 부속(incident) 되어있다.

• 정점 v로 부터 정점 w까지의 경로(path)

  • v0 = v, vk = w인 일련의 정점들 (v0, v1, ..., vk-1, vk)로서 다음 조건을 만족한다.
    • 0≤i≤k-1에 대하여 (vi, vi+1)은 E에 속한다.
    • 이 경로의 길이는 k이다.

• v0, v1, ..., vk 들이 모두 다르면 이 경로를 단순경로(simple path)라고 함.

• 정점 v로 부터 정점 w까지의 경로가 존재하면 w는 v로부터 도달가능(reachable)하다고 함.

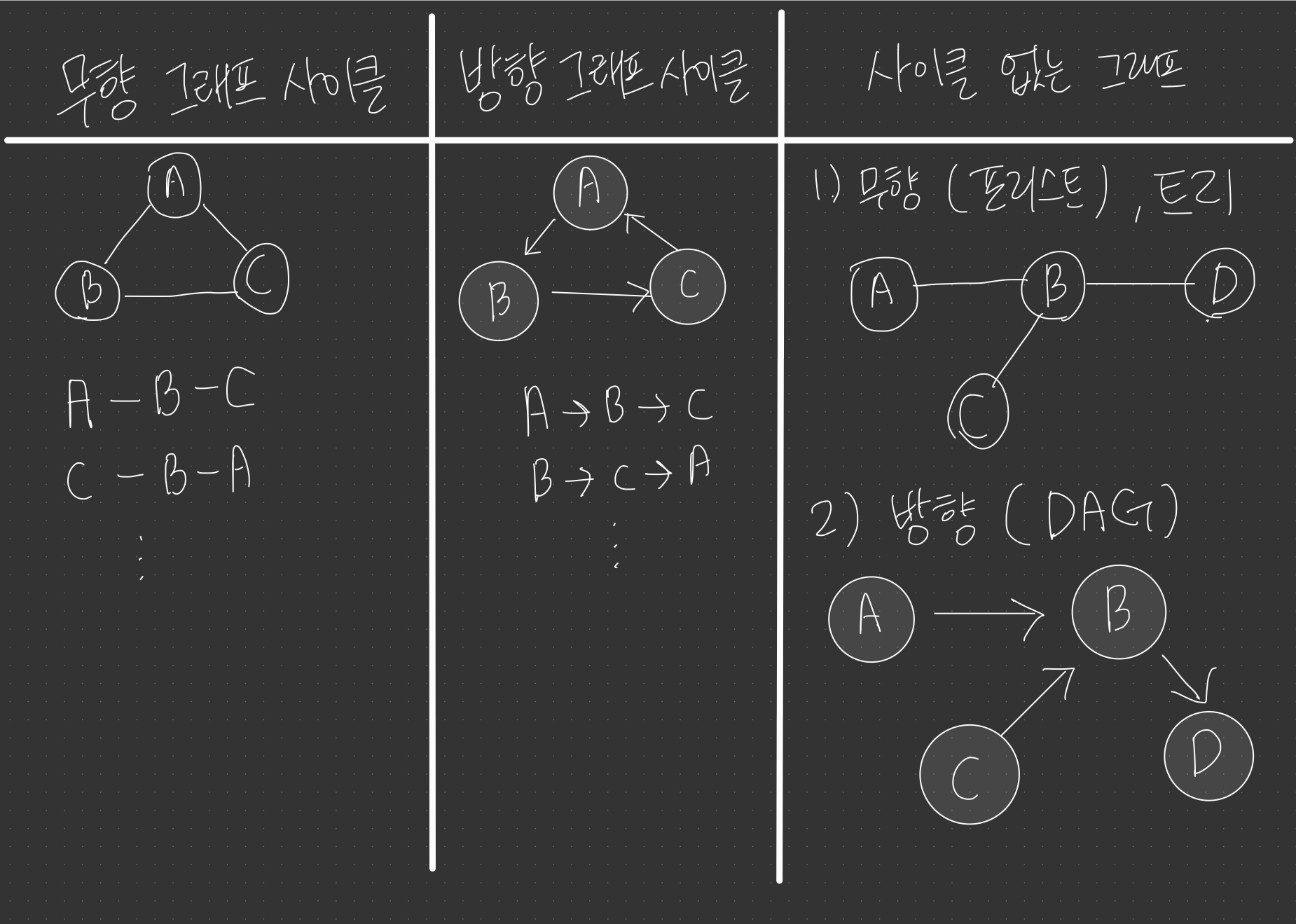
• 사이클

  • 1) 무향(or 양방향) 그래프에서의 사이클
    • 시작 정점과 마지막 정점이 같은 경로 (A -> B , B -> A 모두 가능)
    • ** 단순 사이클 : 시작 정점과 마지막 정점이 같은 것을 제외하고 어떤 정점도 중복되지 않는 사이클
  • 2) 방향 그래프에서의 사이클
    • 시작 정점과 마지막 정점이 같은 경로
    • ** 단순 사이클 : 첫 째 정점과 마지막 정점이 같은 것을 제외하고 어떤 정점도 중복되지 않는 사이클

• 사이클 없는 (무향) 그래프 : 포리스트

• 사이클 없고, 모든 에지가 연결된 (무향) 그래프 : 트리

• 사이클 없는 방향 그래프 : DAG(directed acyclic graph)
  

• 연결 그래프(connected graph) : 임의의 두 정점 u, v에 대하여, u에서 v까지의 경로가 존재하는 그래프

• 강연결 (유향) 그래프 (strongly connected graph) : 임의의 두 정점 u,v에 대하여, u에서 v까지 경로가 존재하는 방향 그래프

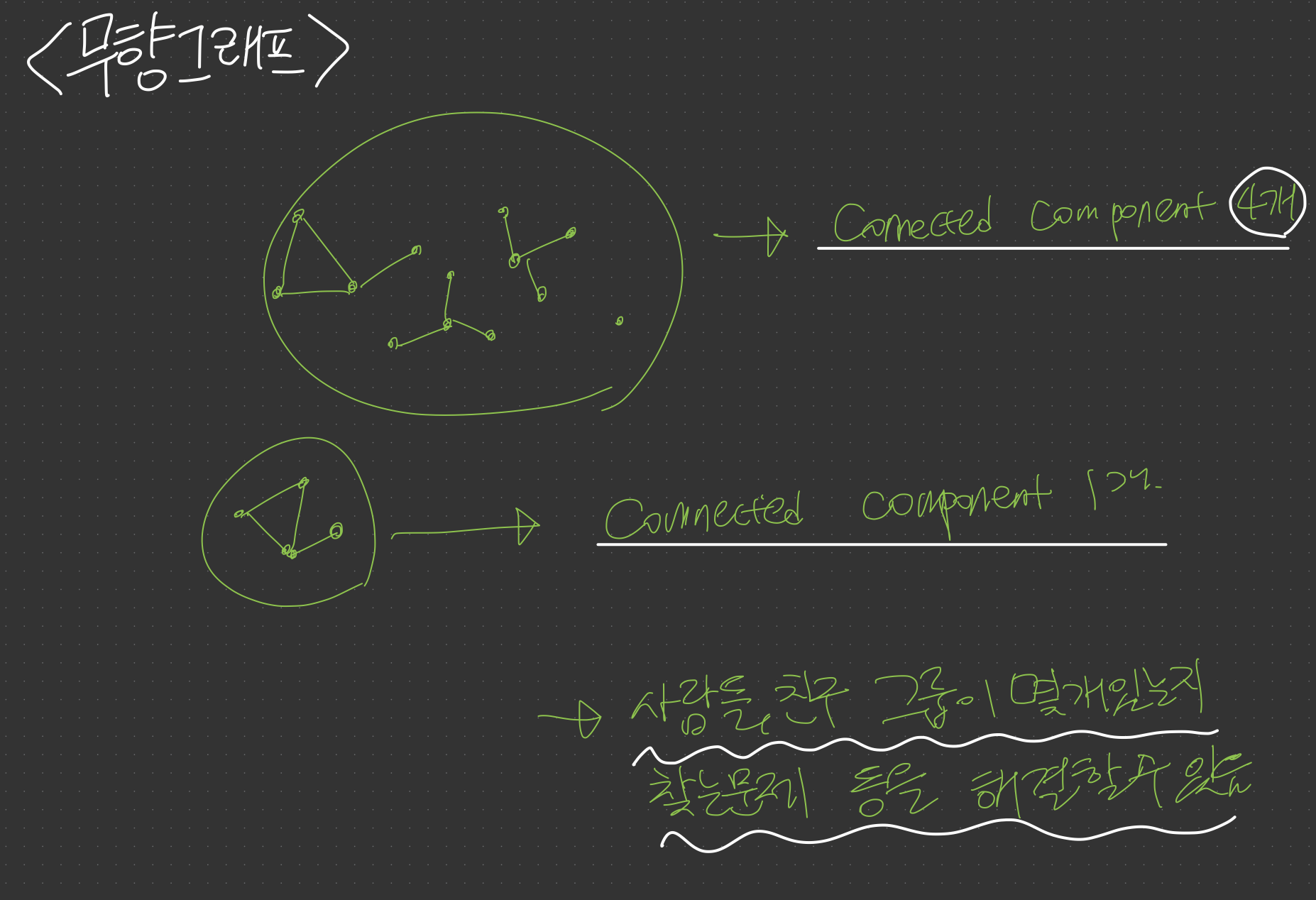
• 그래프 G의 (연결) 성분(connected component) : 그래프 G의 최대 연결 부그래프(maximal connected subgraph of G)

• 방향그래프 G의 강연결성분(strongly connected component) : 방향 그래프 G의 최대 강 연결 부그래프(maximal strongly connected subgraph of G)

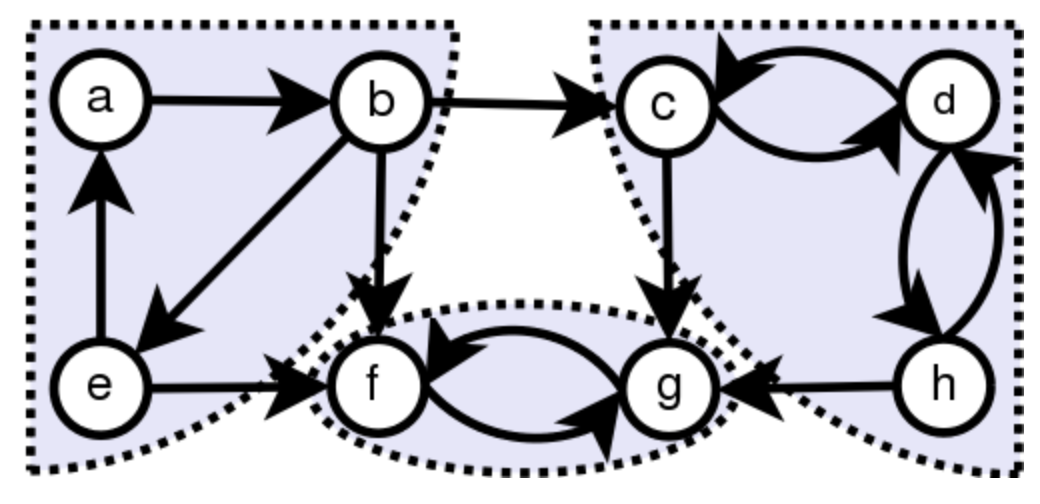
• Strongly Connected Component (SCC)
  • 위 그래프는 정점 8개인 그래프를 3개의 SCC로 분할한 것
  • SCC는 일종의 서브 그래프로써, 하나의 SCC안에는 어떤 정점 u, v 두 개를 골라도 u->v로 가는 직, 간접적인 경로가 존재한다.
  • 또한 Maximal한 성질을 갖는데, 이 말은 각 SCC가 가능한 한 커야한다는 것
    • 예를들어, 우측의 SCC인 {c, d, h}의 하위 집합 중 {c, d} 역시 SCC의 첫 번째 성질은 만족하지만, 여기에 정점 h를 더 추가해도 여전히 성질이 만족되므로 h는 반드시 추가되어 있어야 한다.

참고 : Ries's Naver Blog

---

• 가중치 그래프(weihgted graph) : 에지에 가중치(weight)가 있는 그래프
  • (V, E, W)로 정의됨
    W는 E에서 실수 집합 R로 매핑되는 함수
    • 에지의 가중치 : 비용, 길이, 용량 등 에지의 성질을 나타냄
      (에지 뿐만 아니라 정점에도 가중치를 둘 수 있다.)

---