Python Algorithm class (Greedy Method)

nathan·2021년 5월 10일
algorithmgreedypython
0

Python Algorithm class

목록 보기
16/27
post-thumbnail

Greedy Method (욕심쟁이 방법)

  1. 개요
  2. 동전 교환 문제
  3. 평균적인 대기 시간을 최소로 하는 작업 스케쥴링
  4. 회의실 배정 문제
  5. 배낭 문제

1. 개요

  • 주어진 제약 조건을 만족하는 최적인 해를 구하는 문제(최적화 문제)에 주로 적용하는 방법

  • 최적화 문제란?

    • 제약 조건을 만족하면서 목적함수의 값을 최대 혹은 최소로 하는 해를 구하는 문제

  • 주어진 문제의 해는 일련의 선택 (x1, x2, x3, ..., xn)으로 나타낼 수 있고, 단계별로 하나씩 xi 를 결정함.

  • 각 단계에서, 현재 상태에서 가장 좋다고 판단되는 결정을 함.

    • local optimum이 되는 것을 선택 (한 번 선택한 것을 물리지 않음)

  • 욕심장이 방법은 전체적인 입장에서 보지 않고 현재까지 선택한 상황(현 단계)에서 가장 최선으로 판단되는 결정을 함.

    • 문제에 따라 전체적인 최적 해가 구해질 수도, 구해지지 않을 수도 있음

기본적인 알고리즘

  • C : 후보들의 집합

  • Solution(S) : 특정한 후보들의 집합 S가 주어진 문제의 해인지를 결정하는 함수

  • Feasible(S) : 특정한 후보들의 집합 S가 문제의 해가 될 수 있는 가능성이 있는지를 결정하는 함수

  • Select(S) : 남아 있는 후보들의 집합 C에서 현 상태에서 가장 좋은 후보를 선택하는 함수 (어떤 기준을 갖고 선택하느냐가 굉장히 중요함)

  • pseudo code

Set function Greedy(Set C)
/*C : 후보들의 집합*/
{  S = ø;
   while ( C ≠ ø and !Solution(S)) do // S가 해가 되거나 C가 공집합이 될 때까지 반복
      { x = Select(C); // 현 시점에서 가장 좋은 후보를 선택
        C = C - {x};   // 선택한 후보를 후보들의 집합에서 제외시킴
        if(Feasible(S U {x})) // 해가 될 가능성이 없으면 다시 위로,
           S = S U {x};   // 해가 될 가능성이 있으면 S에 넣기
      }
      if(Solution(S))   
         return S	// 문제의 해라면, S를 반환
      else
         return ø
 }

2. 동전 교환 문제

거스름 돈 교환 문제

  • 여러 단위의 동전들이 주어져 있다. 거스름 돈을 가장 적은 수의 동전으로 교환해주는 방법을 설명하라.

목적 함수 : 사용하는 동전들의 개수
후보들의 집합 C : 1원, 10원, ..., 500원 동전들
함수 Solution : 선택한 동전들의 합이 거스름 돈과 같은 경우 참(True)
함수 Feasible : 선택한 후보들의 합이 거스름 돈을 넘지 않을 경우 참(True)
함수 Selection : 후보들 중 가장 단위가 큰 동전을 선택 (선택의 기준)

ex) 동전 단위 (1원, 7원, 10원) 일때, 14원을 가장 적은 수의 동전으로 교환해주는 방법은?

  • Greedy Method

    • 10원 1개, 1원 4개 -> 총 5개의 동전이 필요

  • 동적 계획법(?)

    • 7원 2개 -> 총 2개의 동전이 필요 (Greedy로는 최적해를 구하지 못한다.)

3. 평균적인 대기 시간을 최소로 하는 작업 스케쥴링

  • n개의 작업들 {1, 2, ..., n}이 있고, 각 작업 i를 처리하는데 걸리는 시간이 p(i)이다.

  • 작업을 처리할 수 있는 server가 하나 있다고 가정한다.

  • 작업들의 평균적인 대기시간을 최소로 하는 작업들의 처리 순서를 정하라.

  • ex-1. n = 6
             처리 순서 ----------------->

    • 작업123456
      처리시간 p(i)341826
      대기 시간03781618

    • 처리하는 작업 순서 : 1, 2, 3, 4, 5, 6

    • 모든 작업의 대기 시간 총 합

      • = 0 + 3 + (3+4) + (3+4+1) + (3+4+1+8) + (3+4+1+8+2)

    • 알 수 있는 점 : 처리 순서가 빠른게 다음 작업들에 영향을 미친다.

    • 따라서 최적인 작업 처리 순서는 처리 시간이 적은 순서대로 처리하면 된다.

  • ex-2. n = 6
             처리 순서 ----------------->

    • 작업351264
      처리시간 p(i)123468
      대기 시간01361016

    • 모든 작업의 대기 시간 총합

      • 0 + 1 + (1+2) + (1+2+3) + (1+2+3+4) + (1+2+3+4+6)
        = 1x5 + 2x4 + 3x3 + 4x2 + 6x1

  • 처리시간이 작은 작업부터 차례대로 처리하면 평균적인 대기 시간이 최소가 된다.

    증명 : 처리 순서를 i1, i2, ..., in이라고 하자.
    이 처리 순서에서 j < k이고 p(ij) > p(ik)인 두 작업 ij, ik가 있다면(순서가 늦지만, 작업시간은 더 작은 경우), 이 작업의 순서를 교환하면, 대기시간 총 합이 늘지 않음을 보이면 된다.
    즉, 처리 순서가 빠르지만 처리 시간이 긴 작업이 앞에 있을 때, 대기시간이 더 크고, 그 순서를 바꿔주면, 대기시간이 줄어든다.

4. 회의실 배정 문제

  • 한 개의 회의실이 있는데, 이를 사용하고자 하는 n개의 회의(activity)들에 대하여 각 회의 i의 시작시간 si와 끝나는 시간 fi가 주어져 있다. 각 회의가 겹치지 않게 하면서, 회의실을 사용할 수 있는 최대수의 회의를 찾아라. 단, 회의는 한 번 시작하면 중간에 중단될 수 없으며, 한 회의가 끝나는 것과 동시에 다음 회의가 시작될 수 있다.

  • ex. n = 12

회의 i시작시간 (si)끝나는 시간 (fi)
114
235
306
457
538
659
7610
8811
9812
10213
111214

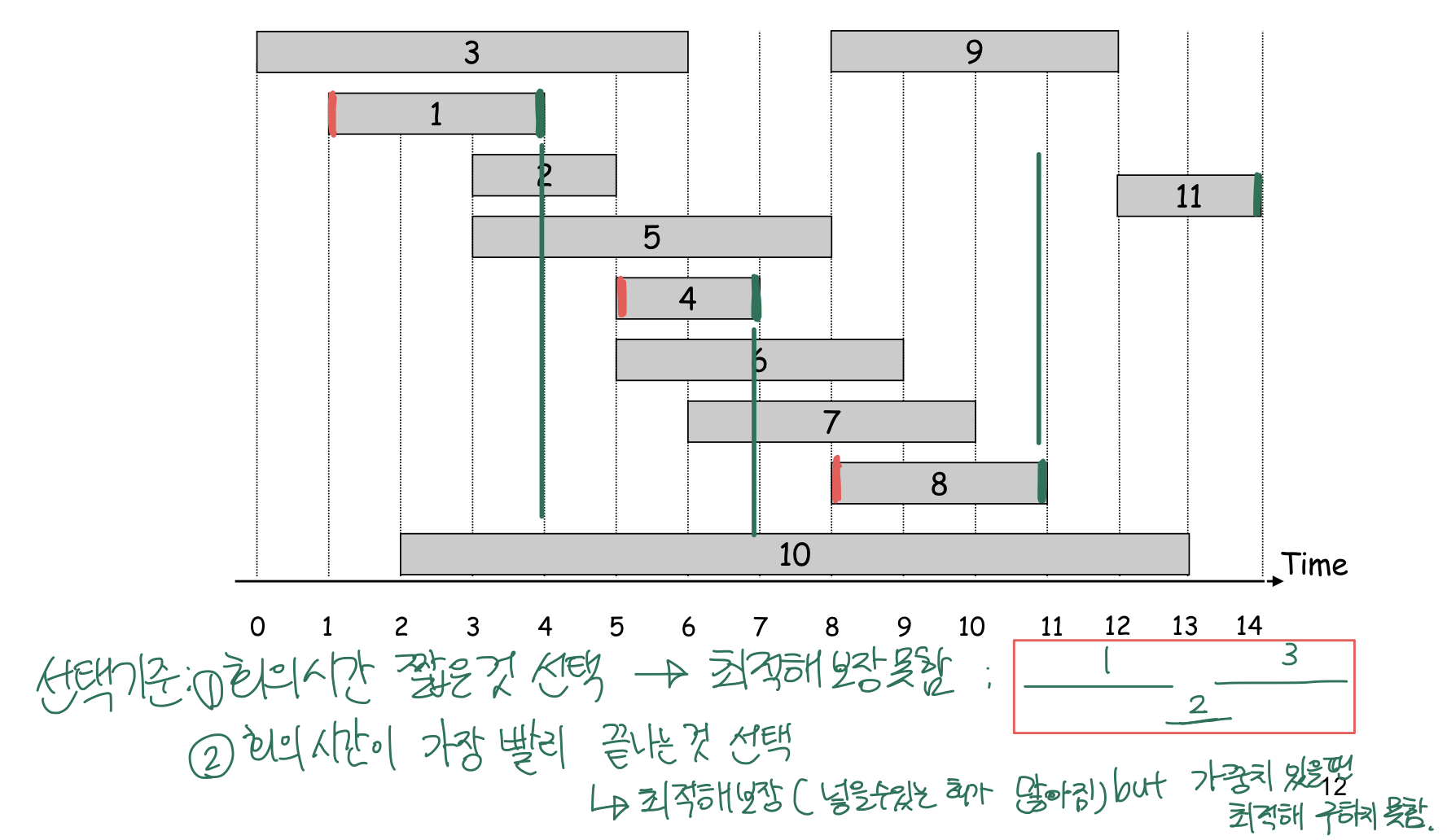
  • 욕심쟁이 방법에 의한 최적해 : Solution = {(1, 4),(5, 7),(8, 11),(12, 14)}

회의실 배정 알고리즘

입력 : S = {(si, fi)|1 ≤ i ≤ n}
출력 : Solution

  • 각 회의 의 끝나는 시간이 증가하는 순서대로 정렬한다.
    (이를 f1, f2, ..., fn 이라 한다.)
  • pseudo code
Algorithm Greedy Schedule(S, n)
   Solution = {1};
   Last = 1;  // 마지막에 선택한 activity
   for(int i = 2; i <= n; i++;)
      if (Si >= flast)
      {
        Solution = Solution U {i};
        Last = i;
       }

성질 1 : 선택 회의 1(끝나는 시간이 가장 빠른 회의)를 포함하는 최적인 해 A가 반드시 존재한다.

  • 증명 : 최적해 A = {i1, i2, ..., ik} : 최적인 해에 들어가는 회의들(끝나는 시간에 의하여 정렬)

  • i1 = 1일 경우 : 성립

  • i1 ≠ 1일 경우 : A' = (A - {i1}) U {1}에 속하는 모든 회의는 서로 겹치지 않는다. (i1을 빼고 대신 1을 넣는다.) 그러므로 회의 1을 포함하는 최적해가 있다.
    -> 욕심쟁이 선택으로 시작하는 최적인 해가 존재한다.

성질 2 : A(회의 1을 포함)가 최적해라면, A' = A - {1}은 회의들 S' = {i가 S의 원소일 때 | si ≥ f1}에 대한 최적해이다.

  • 증명 : A'가 S'에 대한 최적해가 아니라고 하자. 그러면 S'에 대한 최적해 B'에 대하여 |B'| > |A'|이다. B = B' U {1}는 구간들이 겹치지 않는다. 그러면 |B| > |A|가 되어 A가 최적해라는 것에 위배된다.

정리 : 욕심쟁이 방법이 최적 해를 구한다.

증명 : 성질 1,2에 의하여 욕심쟁이 선택을 한 후 남은 문제는 원래 문제와 같은 형태의 최적화 문제가 된다. n에 대한 귀납법에 의하여 매 단계에서 욕심쟁이 선택을 하면 최적인 해를 얻는다.

5. 배낭 문제 (Knapsack Problem)

(1) 기본 배낭 문제

  • 용량이 M인 배낭이 있다. 그리고 이 배낭에 넣고자 하는 물건들이 n개 있다. 물건 i의 무게는 Wi이고, 이것을 배낭에 넣을 경우 Pi의 이익을 얻는다. 배낭에 넣는 물건들의 총 무게의 합이 M이 넘지 않도록 하면서 얻는 이익의 합이 최대가 되도록 하라.

  • 다음 조건을 만족하면서 ∑PiXi(1≤i≤n)를 최대로 하는 (X1, X2, ..., Xn)을 구하라.

    • 조건 : ∑WiXi(1≤i≤n) ≤ M, 0≤Xi≤1(1≤i≤n) (물건을 일부분만 넣을수도 있다.)
    • ∑PiXi : 목적함수

  • ex : n = 3, M = 20, (P1, P2, P3) = (25, 24, 15), (W1, W2, W3) = (18, 15, 10)

가능한 해∑WiXi∑PiXi-
(1/2, 1/3, 1/4)16.524.25일정 비율로 선택, 무게 최대치 충족 X
(1, 2/15, 0)2028.2이익이 큰 것부터 선택, 최적 해 아님
(0, 1, 1/2)2031.5단위무게당 얻는 이익 고려, 최적 해

  • 단위 무게당 얻는 이익 ( = Pi/Wi)

    • 25/18, 24/15, 15/10
    • P2 > P3 > P1

  • pseudo code

Greedy_Knapsack(float P[], float W[], float X[], float M, int n)
/*P와 W는 P[i]/W[i]에 의하여 내림차순으로 정렬되어 있음*/
{  float cu;
   int i;
   for(i = 1; i <= n; i++) {X[i] = 0};
   cu = M; i = 1;
   while((W[i] <= cu) &&  (i <= n))
   {  X[i] = 1;
      cu = cu - W[i];  // 남은 무게
      i += 1;
   }
   if (i <= n)
   X[i] = cu/W[i] // 쪼개서 넣기
}
  • 정리 : 위의 알고리즘 Greedy_KnapSack은 최적인 해를 항상 구한다.

(2) 0/1-배낭 문제 (0/1-Knapsack Problem)

  • 배낭 문제에서 Xi를 0 혹은 1로 제한할 경우 (물건을 넣는 경우, 안 넣는 경우 단 두 가지만 존재) -> Greedy_Knapsack은 최적 해를 항상 구하는 것은 아니다. 이 문제는 NP-Complete이다.

  • ex. n = 3, M = 50, (P1, P2, P3) = (60, 100, 120), (W1, W2, W3) = (10, 20, 30)

    • Greedy_Knapsack에 의한 해 (X1, X2, X3) = (1, 1, 0)
      • 최적해를 보장하지 못함. (부분 짐을 담지 못하기 때문)
    • 최적해 : (X1, X2, X3) = (0, 1, 1)
      • 동적 계획법 혹은 백트래킹으로 해결이 가능.

  • x : 1, 2, ..., i, ..., n

  • f(i, X) : (1, 2, ..., i) 물건들 중 넣든, 넣지 않든 최대 용량

    • X : 용량

  • 목적 함수의 해 : 가방에 넣을 수 있는 최대 이득

  • i를 Knapsack에 넣는 경우 : Pi, Wi를 제외한 나머지
    • X - Wi (1, 2, ..., i-1) => Pi + f(i-1, X-Wi) (Wi ≤ X)
  • i를 Knapsack에 넣지 않는 경우 => f(i-1, X)

  • f(i, X) = max{Pi + f(i-1, X-Wi), f(i-1, X)}

  • f(n,m) 일 때 O(nm)만큼의 시간 복잡도를 갖는다.

    • (n개의 짐 검사할 때, m가지의 경우(넣든, 넣지않든 하는 짐) 고려) ... m : 용량

  • Polynomial time Algorithm 처럼 보이나 m이 만약 10^9이면, 전체 수행시간이 엄청나게 증가함을 알 수 있다.

    • m에 따라 달라짐 -> NP-Complete 문제이다. (입력 값에 따라 좌우됨)

NP-Complete (NP 완전 문제)

(Nondeterministic Polynomial)

  • 문제의 종류는 크게 두 가지로 나누어 생각할 수 있다.

    • 1) 풀 수 없는 문제들 (Unsolvable, Undecidable)
      • ex. 힐버트의 10번째 문제
    • 2) 풀 수 있는 문제들 (Solvable, Decidable)
      • (1) 현실적인 시간 내에 풀 수 없는 문제들
        • 여기에 NP-Complete가 속한다.
      • (2) 현실적인 시간 내에 풀 수 있는 문제들
        • ex. 최소 신장 트리 문제, 최단 거리 문제 등 (일반적인 알고리즘 문제)

  • 현실적인 시간은 무엇을 의미하는가? (시간 복잡도의 측면)

    • 다항식 시간을 의미 (Polynomial time Algorithm으로 해결 가능)
      • 입력 크기 n의 다항식으로 표시되는 시간
        • ex. 3logN * N^2

  • 비다항식 시간 (Polynomial time Algorithm으로 해결 안됨)

    • 지수 시간이나 계승 시간 등을 의미 (NP-Complete)
      • ex. 2^n (지수 시간)
      • ex. n! (계승 시간)
profile
nathan
나는 날마다 모든 면에서 점점 더 나아지고 있다.
이전 포스트

Python Algorithm class (Dynamic Programming - 5)

다음 포스트

Python Algorithm class (Graph - 1)

0개의 댓글