RND (Exploration by Random Network Distillation)

OpenAI에서 발표한 Exploration에 대한 논문. 18년도까지 여러 강화학습 알고리즘이 있었지만 Reward가 Sparse한 환경인 몬테주마의 복수에서 인간의 성능을 최초로 넘은 방법이다.

몬테주마의 복수 게임의 모습

Abstract

• 이 논문에서 강화학습을 휘한 Exploration bonus를 소개한다.
• 이 Exploration bonus는 적용하기 쉽고, 동작하는데 최소의 오버헤드가 든다.
• 이때 bonus는 고정되고 랜덤하게 초기화된 네트워크로부터 얻은 관측(observations)의 특징(feature)을 예측하는 신경망의 에러를 말한다.
• intrinsic and extrinsic reward를 적절하게 결합하여 사용한 flexibility에 대한 method를 소개한다
• 이 알고리즘을 통해 몬테주마의 복수에서 SOTA를 달성하였고 인간의 성능을 뛰어넘게 된 첫번째 방법으로 의의를 가진다.

1. Introduction

기존의 제한 사항들

• 강화학습은 Policy의 반환값(return)의 기댓값을 극대화 하도록 동작한다. 보상(reward)가 밀집된(dense)한 경우, 대체적으로 잘 학습한다. 하지만 보상이 뜨문뜨문한(sparse) 경우, 학습시키기 어렵다.
• 실제 세계에서도 모든 보상들이 밀집된 경우는 드물다. 따라서 보상이 드문 경우에도 잘 학습하기 위한 방법이 필요하다.
• 18년 당시 RL에서는 어려운 문제들을 풀기위해 환경을 병렬적으로 크게 만들고 경험들을 샘플링하여 얻었지만 이러한 방법은 당시에 소개된 exploration 방법들에 대해서는 적용하는데 어려움이 있었다.

제시하는것

간단하고 고차원의 관측에서도 잘 동작하는 Exploration bonus를 소개한다. 이 알고리즘은 policy optimization과 함께 적용할 수도 있고, 계산 효율적이기도 하다.

아이디어

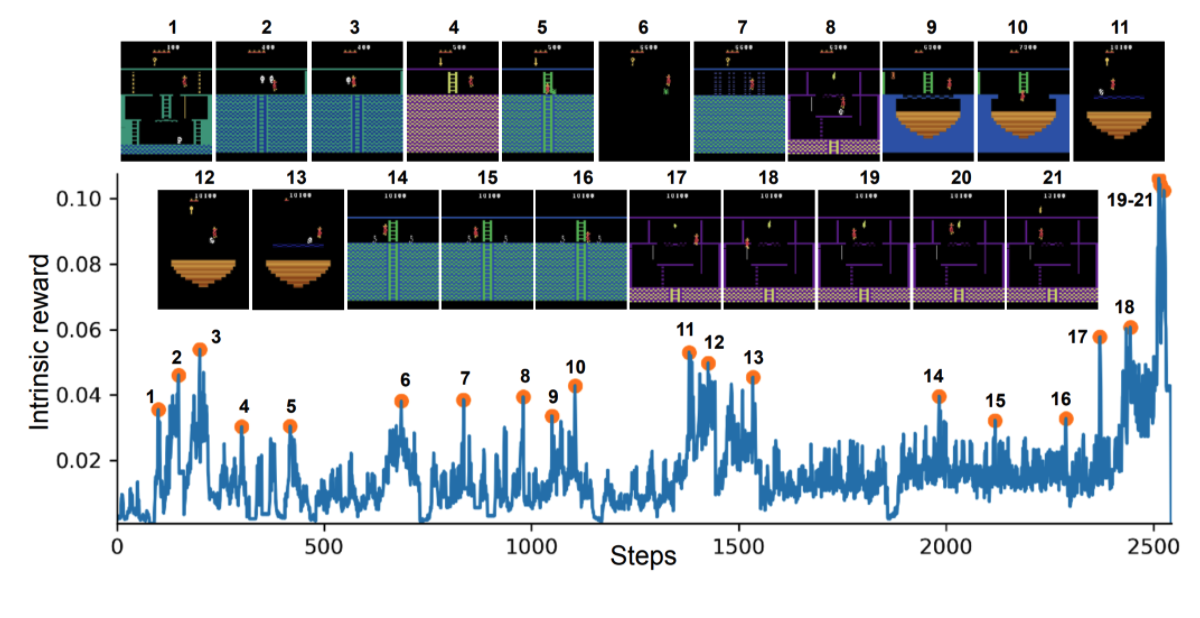
유의미한 이벤트가 발생할 때 내부 보상이 높은 것을 볼수 있다. (2, 8, 10, 21) 은 life를 잃을 때, (3, 5, 6, 11, 12, 13, 14, 15) 는 적을 아슬아슬하게 피할 때, (7, 9, 18) 은 어려운 장애물을 피할때, 그리고 (19, 20, 21) 은 아이템을 습득할 때

이 논문에서 제시된 Exploration bonus는 신경망에서 학습된 것들과 유사한 예들에 대해서 prediction error가 현저하게 낮은 것에서 아이디어를 얻었다.

새로운 경험들의 참신함을 측정하기 위해, 에이전트의 과거 경험들에 대해 학습한 네트워크의 prediction error를 사용하였다.

prediction error를 극대화 하는것의 문제

이전에 많은 저자들이 지적했듯이 prediction error를 최대화 하는 에이전트의 경우는 prediction problem의 답이 입력의 확률적 함수인 transition들에 대해 끌리게 된다.

예를들어 Noise TV 와 같은 예가 있다. 현재 obsevation에서 다음 observation을 예측하는 prediction problem이 있고, 이때 에이전트가 prediction error를 극대화 하도록 행동한다면, 확률적 전환(stochastic transitions)을 찾도록 하는 경향이 있다.

그 예로 무작위로 변하는 아래와 같은 화면인 Noise TV와 무작위로 동전을 던지는 이벤트와 같은 것들이 있다.

문제를 극복하기 위한 대안

논문의 저자들은 적절하지 않은 stochasticity에 대한 대안을 제시한다. 답이 그것의 입력에 deterministic function인 prediction problem을 exploration bonus으로 정의하면서 대안으로 제안한다.

대안으로는, 현재 Observation에 대해서 output을 fixed randomly initialized network를 사용해서 예측한다는 것이다.

강화학습에서 어려운 게임들 🤦‍♂️

Bellemare의 2016년 논문에서 보상이 드물고 탐색이 어려운 게임들을 확인했다. 그 게임들로는 Freeway, Gravitar, Montezuma's Revenge, Pitfall, Private Eye, Solaris, Venture 들이 있고, 어떤 경우에서는 단 하나의 긍정보상도 찾지 못했다.

그 중에서도 어려운 몬테주마의 복수

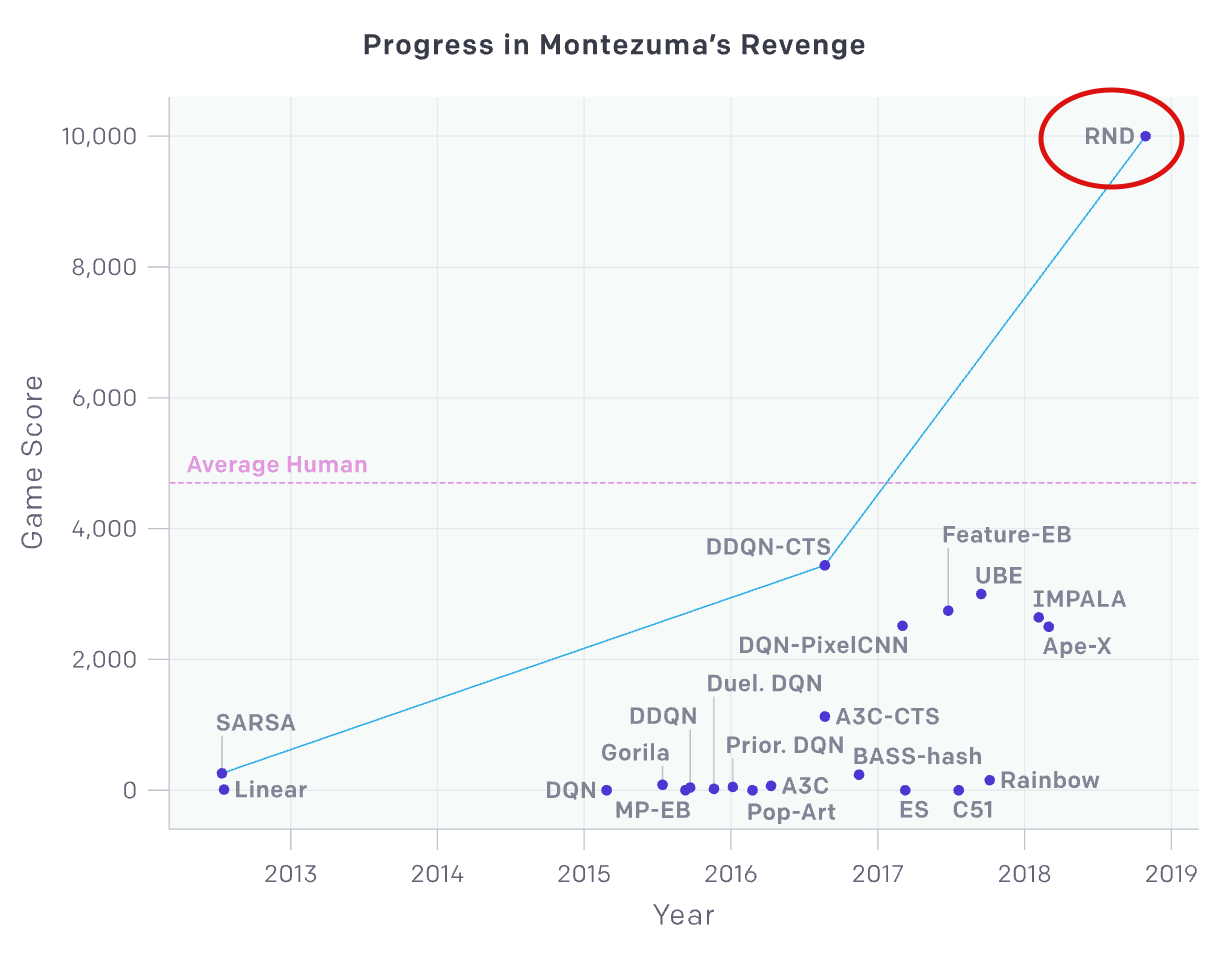
몬테주마의 복수는 강화학습에서 어려운 게임으로 여겨진다. 게임에서 치명적인 장애물을 피하기 위해 다양한 게임스킬들에 대한 조합들이 필요하고, 최적의 플레이를 하면서도 보상이 수백 스텝 이상 떨어져 있기 때문에, 보상을 찾기에 어려운 과제로 여겨진다.

몇 논문들에서 꽤 좋은 성과를 거두었지만, expert demonstrations와 emulator state에 대한 접근 없이는 가장 좋은 성과가 전체 방의 절반만 찾아내었다.

논문에서 발견한것 🔍

extrinsic reward 없는 경우

• extrinsic reward를 무시하여도 agent가 RND exploration bonus를 극대화 하도록 한다면 일관되게 몬테주마의 복수 게임에서 절반 이상의 방을 찾았다.

extrinsic reward와 exploration bonus 결합

• exploration bonus와 extrinsic reward를 결합하기 위해서 수정된 PPO(Poximal Policy Optimization)을 제안한다. 수정된 PPO는 2개의 보상을 위해 2개의 value head를 사용한다.
• 서로 다른 보상(reward)에 대해 서로 다른 discount rate를 사용하고, episodic과non-episodic 반환값(return)을 결합한다.

성과

first level에서 종종 몬테주마 게임에서 24개의 방 중에서 22개를 찾았고, 이따금씩 클리어 하기도 했다. 그리고 같은 방법으로 Venture와 Gravitar에서 SOTA를 달성하였다.
Venture

Gravitar

2. Method

2.1 Exploration Bonuses

explorration bonus는 보상 $e_t$가 드문 환경(environment)에서도 agent가 exploration 할수 있도록 장려하는 방법.

• 보상 $e_t$는 새로운 보상 $r_t= e_t + i_t$로 대체
• 이 때, $i_t$는 exploration bonus로 time $t$의 transition과 연관있다.

장려를 위한 방법

agent가 novel state들을 탐색하도록 장려하는 방법은, 자주 방문하는 것들보다 novel state들에 대해 $i_t$ 값이 더 커지도록 한다.

1) Count-Based

상태에 대한 제한 수를 가진 tabular setting에서는 $i_t$ 를 방문수 $n_t$에 따라 점점 줄어들도록 정의 할수 있고 이전 논문들에서 사용 되었다.

• $i_t = 1/n_t(s)$
• $i_t = 1/\sqrt{n_t(s)}$

non-tabular case에서는 대부분의 상태들이 한번 정도만 방문하기 때문에 위와 같이 적용하는 것은 쉽지 않다. 그래서 pseudo-count와 같은 방법들이 있다. pseudo-count는 이전에 방문했던 상태들과 유사하다면 과거에 방문한적이 없는 상태들에 대해 양수인 값을 줄 수 있는 density model로부터 얻을 수 있다.

2.2 Random Network Distollation

이 논문에서는 랜덤하게 생성된 prediction problem에 대한 다른 접근 방법을 소개 한다.target network와 predictor network와 같이 2개의 네트워크를 사용한다.

• $target$ network: fixed random initialized target network , prediction problem set
• $predictor$ network: agent에 의해 수집된 데이터로 학습하는 네트워크

target network
$f: O {\rightarrow} R^k$

predictor network
$\hat{f}: O {\rightarrow} R^k$

위와 같이 구하고 $||\hat{f}(x;\theta)-f(x) ||^2$ 에러값을 최소화 하도록 그래디언트 디센트 방법을 통해 predictor의 파라미터 $\theta_{\hat{f}}$을 학습한다.

위 방법이 target network인 randomly initialized neural network를 이용해서 predictor network를 학습 시키는 과정이다.

prediction error는 predictor가 학습한것과 다른 novel state에 대해서 높은 값을 가지게 될것이다.

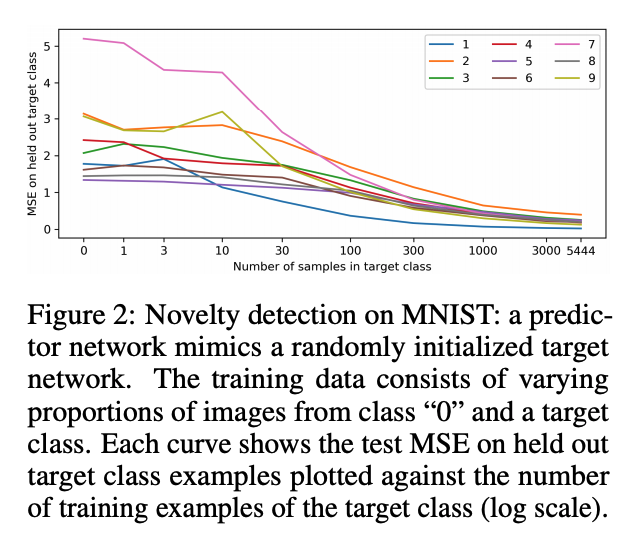
위 figure2에서는 target class에서 training example들의 수에 대해 test errorr가 감소하는것을 보여주고 novel state를 탐지할 수 있는데 사용할 수 있음을 알려준다.

predictor가 랜덤한 target network를 완전히 모사할 수 있을거라는 반대 의견도 있지만 위 figure를 통해 아님을 보였다.

2.2.1 Source of Prediction Errors

일반적으로 prediction error 들은 아래 요소들로부터 나온다.

1. Amount of training data

predictor가 전에 학습한 example들과 다를수록 prediction error가 높다

2. Stochasticity

target function이 확률적이기 때문에 prediction error가 크다. stochastic transition들은 forward dynamic prediction과 같은 에러들의 원인이다.

3. Model misspecification

필요한 정보가 부족하거나 모델이 target funtion의 복잡도에 맞추기 위해 제한적인 경우

4. Learning dynamics

predictor가 target funtion을 근사 하는 과정에서 최적화를 실패했을때,

• 2번째 요소는 noisy TV 문제를 야기하고 3번째 요소도 적절하지 않기 때문에 RND에서는 요소 2,3을 제거한다. 3 since the target network can be chosen to be deterministic and inside
  the model-class of the predictor network.

2.2.2 Relation to Uncertaionty Quantification

RND의 prediction errror는 불확실한것을 수량화하는 것과 관련이 있다.

RND prediction error

• Data distribution $D={x_i,y_i}_i$에 대한 regression 문제로 볼수 있다.
• 베이지안 설정에서 매핑된 $f_{\theta}$의 파라미터들에 대한 이전 $P(\theta^*)$를 고려하고 evidence 들에 대해 업데이트 한 후에 뒤쪽을 계산한다.
• $p({\theta})$로 부터 나온 ${\theta}^*$에 대해 함수 $g_{\theta}=f_{\theta}+f_{\theta^*}$의 분포가 되는 F
• ${\theta}$는 기대되는 prediction error를 최소화 한다
• ${\theta} = \underset{\theta}{argmin}E_{(x_i,y_i)~D}||f_{\theta}(x_i)+f_{\theta^*}(x_i) -y_i||^2 + R({\theta})$
• $R({\theta})$ 는 이전 논문에서 나온 정규화 용어. Osbands는 18년 눈문에서 앙상블 F가 수식에 대한 근사라고 함.

regression target $y_i$가 0이 된다면

• 최적화 문제는 $E_{(x_i,y_i)~D}||f_{\theta}(x_i)+f_{\theta^*}(x_i)||^2$는 distilling a randomly drawn function과 동일 하다고 볼수 있다.
• 이런 관점에서 predictor와 target network의 결과의 각 좌표들은 앙상블의 멤버로 반응하며 MSE 는 앙상블의 예측된 variance가 될 수 있다.
• 위 과정을 통해 distillation error 불확성에 대한 계량을 할 수 있음을 보인다.

2.3 Combining Intrrinsic and Extrinsic Return

이전 실험들에서 intrinsic reward만 non-episodic 문제에서 다루엇으며, 더 나은 exploration 결과를 보였다. 하지만 이 방법에서는 게임이 오버되어도 리턴이 종료 되지 않았다는 문제가 있었다.

• 저자들은 시뮬레이션 환경에서 더 자연스러운 exploration 방법을 보인다.
• agent 의 intringic return은 미래에 찾을 수 있는 모든 novel state들에 대해 관련 있어야 하기 때문에.
• 그리고 이 방법이 인간이 게임에서 explore 하는 방법과 가깝다고 주장한다.

extrrinsic reward에 대한 non-episodic return
non-episodic return 에 대해 non-episodic return을 사용하는것은 전략이 게임의 시작과 가까운 보상이 이용(exploited)되도록 할 수 있으며, 고의적으로 게임을 종료시키고 다시 게임의 시작으로 돌아가는 사이클이 반복 될 수 있다.

non-episodic stream value에서 intrinsic reward $i_t$와 epsodic stream에서 extrinsic reward $e_t$의 조합을 평가하는 방법은 불분명 하다.

• 그래서 저자들의 방법은 return들이 linear인지 관찰한다. 이때 $R = R_E+R_I$을 return으로 사용하였다.
• 따라서 2개의 value 헤드 $V_E$와 $V_I$ 값을 각각의 return들을 사용해서 fit 할수 있고
• 위의 값을 조합한 $V=V_E+V_I$도 사용할 수 있다.

2.4 Reward and Observation Normalization

reward

prediction error를 exploration bonus로 사용하는것이 보상의 크기가 환경에 따라, 시간에 따라 크게 다르기 때문에 모든 환경에서 동작하는 하이퍼파라미터를 찾는 것은 어려운 부분이 있다.

일정한 크기의 reward를 유지하기 위해서 intrinsic reward를 intrinsic reward의 표준편차들에 대한 추정치로 나누어 주어 normalization 과정을 거친다.

observation

랜덤 신경망을 사용할 때는 파라미터들이 고정되고 다른 데이터 셋들에 대해서도 조정되면 안되기 때문에 observation normalization이 중요하다. normalization이 부족하면 임베딩의 분산이 극단적으로 낮아지고 입력에 대한 정보가 조금만 전달되는 결과가 발생할 수 있다.

• 이러한 문제를 해결하기 위해 continuous control 문제에서 사용하는 observation normalization scheme을 사용하고, 각 dimension에 running mean을 빼고 running standard deviation을 나누어 값을 normalization.
• 그 후 값이 -5와 5사이에 오도록 잘라준다.
• predictor와 target network는 동일한 obsevation nomalization, policy network에 대해서는 사용하지 않는다.

References

• https://arxiv.org/pdf/1810.12894.pdf
• https://kr.endtoend.ai/slowpapers/rnd
• https://bluediary8.tistory.com/37
• https://seolhokim.github.io/deeplearning/2019/10/11/Exploration-by-random-network-distillation-review/
• https://openai.com/blog/reinforcement-learning-with-prediction-based-rewards/