Multi-step TD

Model-Free prediction

MDP를 모르는 경우에도 어떻게 prediction을 하고 어떻게 control을 할지.
prediction은 value를 찾는 문제. MC와 TD가 있다.

MC(Monte-Carlo Leanring)

에피소드를 끝까지 수행하고 얻은 결과에 대해 평균으로 value를 취한다. 실제 수행한 값의 평균을 취한다.

• 목표: Policy $\pi$ 를 따라 수행한 에피소드로 부터 $V_{\pi}$를 학습하는것
  
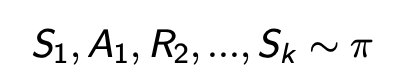
• return은 discounted reward의 총합
  
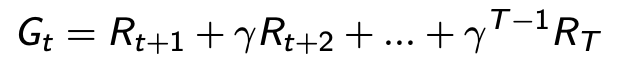
• $(V_t)$ 는 실제 에피소드가 끝나고 얻은 반환 값 $G_t$을 향해 업데이트

  $V(S_t) {\leftarrow} V(S_t) + \alpha( G_t - V(S_t))$

TD(Temporal-Difference Learning)

에피소드를 끝까지 수행하지 않고, 추측한 값을 통해 보상을 업데이트 하는것.

$TD(0)$

: 한스텝 앞(t+1)을 보고 현재(t)의 $V(S_t)$를 업데이트 하는것. n-step TD는 N 스텝 앞을 보고 현재의 $V(S_t)$를 업데이트 하는것. 현재의 가치를 예측한 추측값을 한스템 더 가서 추측한 값으로 업데이트를 하는것.

$V(S_t) {\leftarrow} V(S_t) + \alpha(R_{t+1} + \gamma V(s_{t+1}) - V(S_t))$

• TD target: $R_{t+1} + \gamma V(s_{t+1})$
• TD error: $R_{t+1} + \gamma V(s_{t+1}) - V(S_t)$

MC와 TD의 차이

MC

• complete
• function approximation에서 $V_{\pi}(S)$에수렴을 잘한다.
• 초기값에 덜 민감
• 사용과 이해에 편하다.

TD는

• in-complete
• function approximation에서 $V_{\pi}(S)$에 수렴을 못할 수도 있다.
• 초기값에 민감

N-Step TD

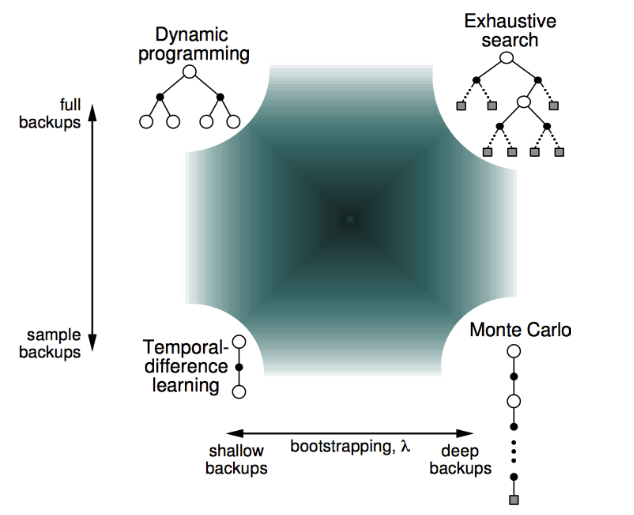
• Bootstrapping: 추측치로 추측치를 업데이트 하는것을 bootstrapping 이라 한다. 업데이트에 etstimate가 포함된다. (Depth 관점)
• Sampling: 탐색에 있어 너비에 대해 샘플링 하였는지. (Width 관점)
  

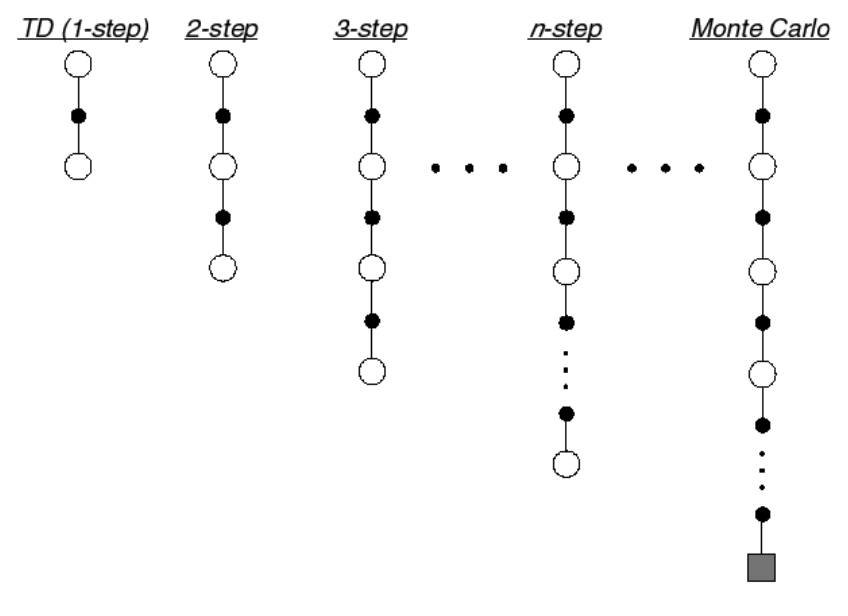
N-step TD

N 스텝의 값으로 업데이트를 하는것이 n-step TD

TD와 MC의 반환값

• n=1 (TD) ---- $G^{1}_t = R_{t+1} + \gamma V(S_{t+1})$
• n=2 ---- $G^{2}_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 V(S_{t+2})$
  ...
• n=$\infin$ (MC) ---- $G^{\infin}_t = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-1} V(S_{T})$

n-step의 반환값

• $G^{(n)}_t = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n-1} R_{t+n} +\gamma^{n} V(S_{t+n})$

이외의 TD

• Average n-step
• TD($\lambda)$
  • forward-view TD($\lambda)$
  • backward-view TD($\lambda)$

업데이트 방법

• Online: 에피소드의 매 스텝마다 업데이트가 되는것
• Offline: 에피소드가 끝나고 난 후 업데이트 되는것

Reference

• David Silver, RL lecture4: model-free prediction
• Random Walk Codee
• 팡요랩 강의