동적계획법

전체 문제를 작은 문제로 단순화한다. -> 부분 문제를 정의한다.
재귀적인 구조를 활용할 수 있는 점화식을 만든다. -> 점화식을 만든다.
작은 문제를 해결한 방법으로 전체 문제를 해결한다. -> 문제를 해결한다.

전체 문제를 작은 문제로 단순화한 다음 점화식으로 만들어 재귀적인 구조를 활용해서 전체 문제를 해결하는 방식

by 동적계획법

1003

1003번 : 피보나치 함수

#include <iostream>
using namespace std;

int fibo[50] = { 0, 1, };

int fibonacci(int n) {
    if (n == 0) {
        return fibo[n];
    }
    else if (n == 1) {
        return fibo[n];
    }
    if (fibo[n] != 0)
        return fibo[n];
    else {
        return fibo[n] = fibonacci(n - 1) + fibonacci(n - 2);
    }
} 

int main() {
    int T;
    cin >> T;
    int temp;
    for (int i = 0; i < T; i++) {
        cin >> temp;
        if (temp == 0)
            cout << "1 0" << '\n';
        else
            cout << fibonacci(temp - 1) << " " << fibonacci(temp) << '\n';
    }

}

🎈 배열 초기화

0과 1 인덱스에 각각 피보나치 수열함수를 불러올때마다 더해질 0와 1을 저장한다. {0, 1, } 은 인덱스 0에 0, 인덱스 1에 1을 저장하고, 그 뒤에는 0으로 모두 초기화한다는 뜻이다.

🎈 피보나치 수열함수

int fibonacci(int n) {
    if (n == 0) {
        return fibo[n];
    }
    else if (n == 1) {
        return fibo[n];
    }
    if (fibo[n] != 0)
        return fibo[n];
    else {
        return fibo[n] = fibonacci(n - 1) + fibonacci(n - 2);
    }
} 

만약 n이 0이면 인덱스 0을 리턴하고, n이 1이면 인덱스 1을 리턴하여 결과리턴값에서 각 int값이 더해지도록 구현한다.

🎈 메인 함수

int main() {
    int T;
    cin >> T;
    int temp;
    for (int i = 0; i < T; i++) {
        cin >> temp;
        if (temp == 0)
            cout << "1 0" << '\n';
        else
            cout << fibonacci(temp - 1) << " " << fibonacci(temp) << '\n';
    }

temp가 0일때는 피보나치 수열 합의 결과값이 0이므로 1 0을 출력하도록한다.
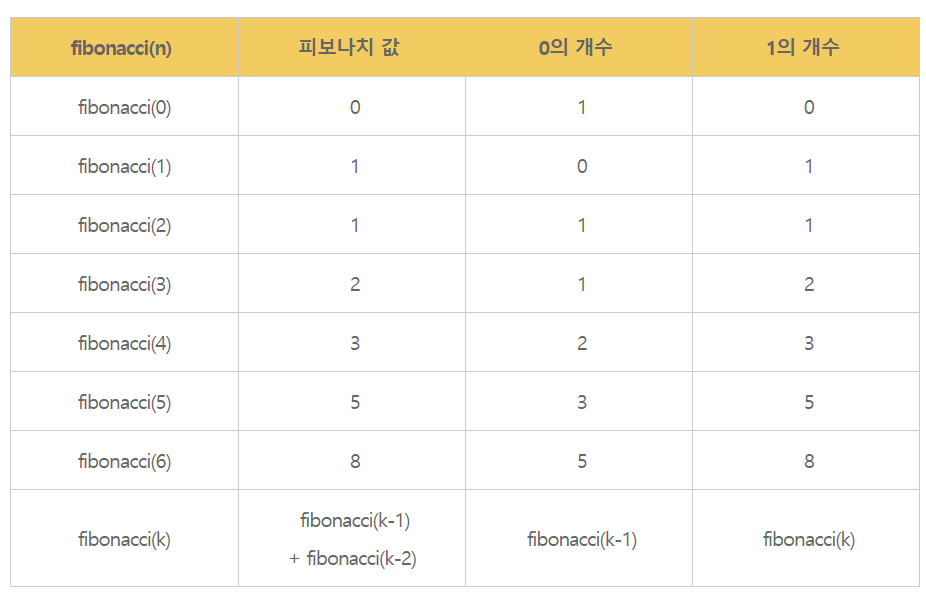
그 외의 경우에서는 규칙성을 찾아보았을 때, 0을 출력하는 횟수는 fibonacci(temp - 1), 1을 출력하는 횟수는 fibonacci(temp)에 해당한다.

🔔 규칙성