9184
🎈 해결방법
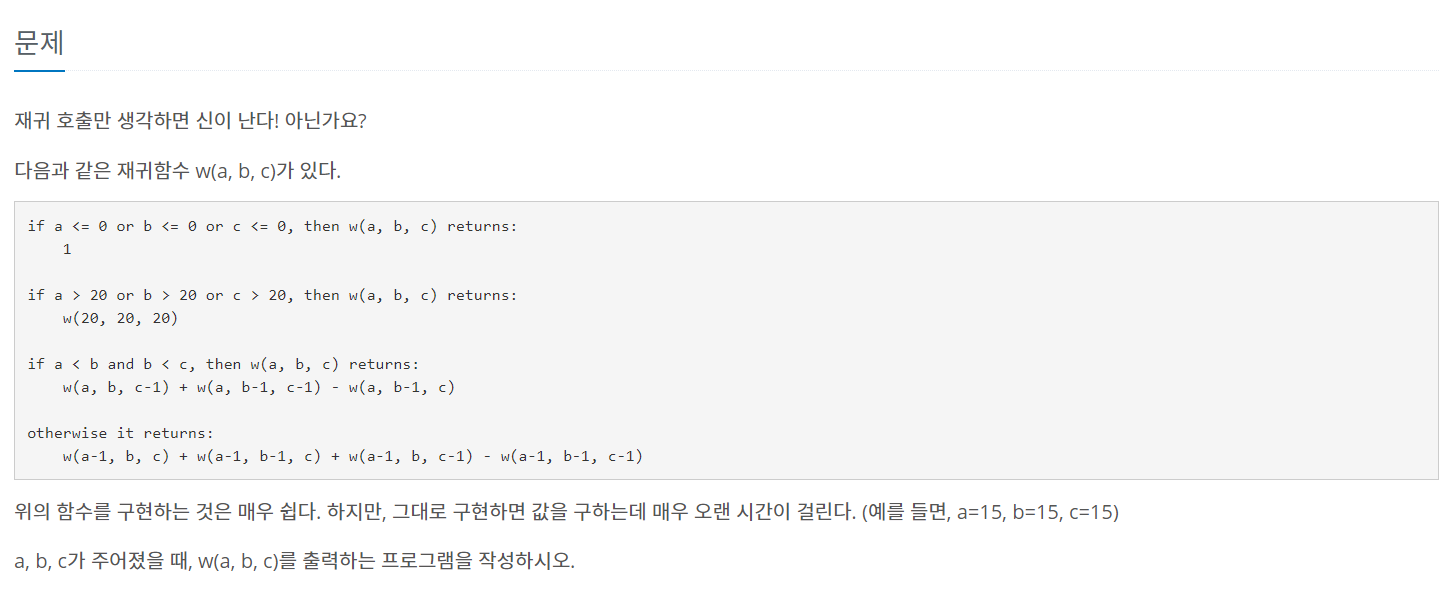
동적 계획법을 사용하여 구현해 주었다. w 함수를 도출하기 위해 매번 재귀를 불러와 시간을 증가하기 대신, 그때그때 각 상태에서의 함수값을 arr[][][]에 저장하여 필요할 때 불러주었다.
그 외 함수 형태는 문제에서 그대로 주어져 비교적 쉬웠다!
#include <iostream>
using namespace std;
int arr[50][50][50];
int w(int a, int b, int c) {
if (a <= 0 || b <= 0 || c <= 0)
return 1;
if (a > 20 || b > 20 || c > 20)
return w(20, 20, 20);
int& result = arr[a][b][c]; // 각 상태에서의 함수값 저장
if (result != 0)
return result;
if (a < b && b < c)
result = w(a, b, c - 1) + w(a, b - 1, c - 1) - w(a, b - 1, c);
else
result = w(a - 1, b, c) + w(a - 1, b - 1, c) + w(a - 1, b, c - 1) - w(a - 1, b - 1, c - 1);
return result;
}
int main() {
int a, b, c;
while (true) {
cin >> a >> b >> c;
if (a == -1 && b == -1 && c == -1)
break;
cout << "w(" << a << ", " << b << ", " << c << ") = " << w(a, b, c) << endl;
}
}그리디 알고리즘
그리디 알고리즘이란, 현재의 상황에서 가장 최선의 방법을 선택하는 알고리즘이다! 그래서 항상 실제 최선의 경우를 선택하진 않는다. 예를 들어, 트리구조에서

이 트리구조에서 그리디 알고리즘을 따른다면 3 - 4 - 7 순서로 선택하여 7을 가장 큰 숫자로 고르게 되는 것이다. 그러나 실제 최댓값은 9인 상황이다.
동적계획법은 모든 경우를 효율적으로 다 실행해보는 방식으로, 그리디 알고리즘과 대비된다.
11047
🎈 해결방법
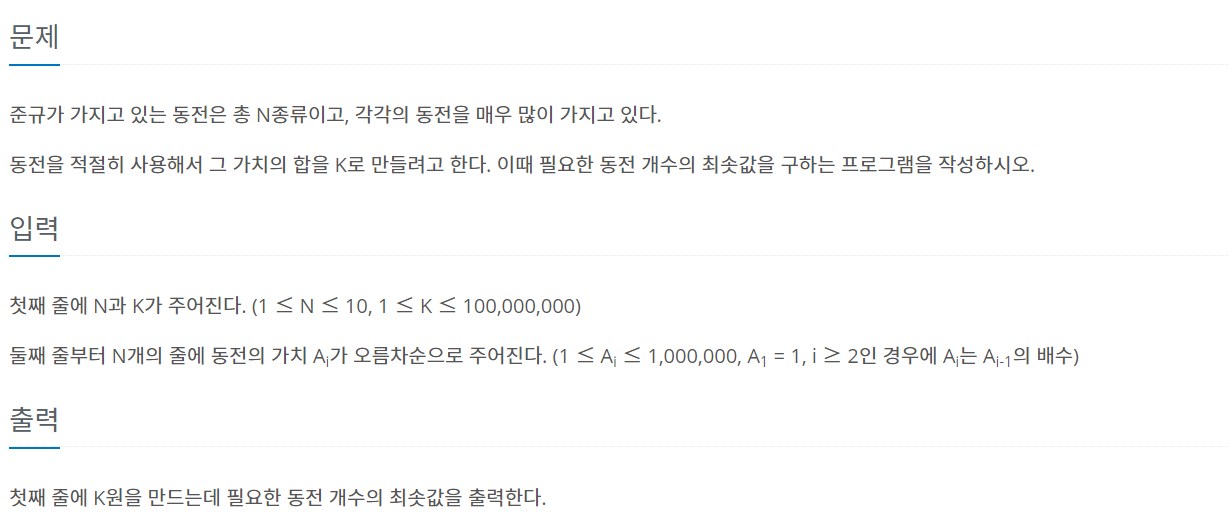
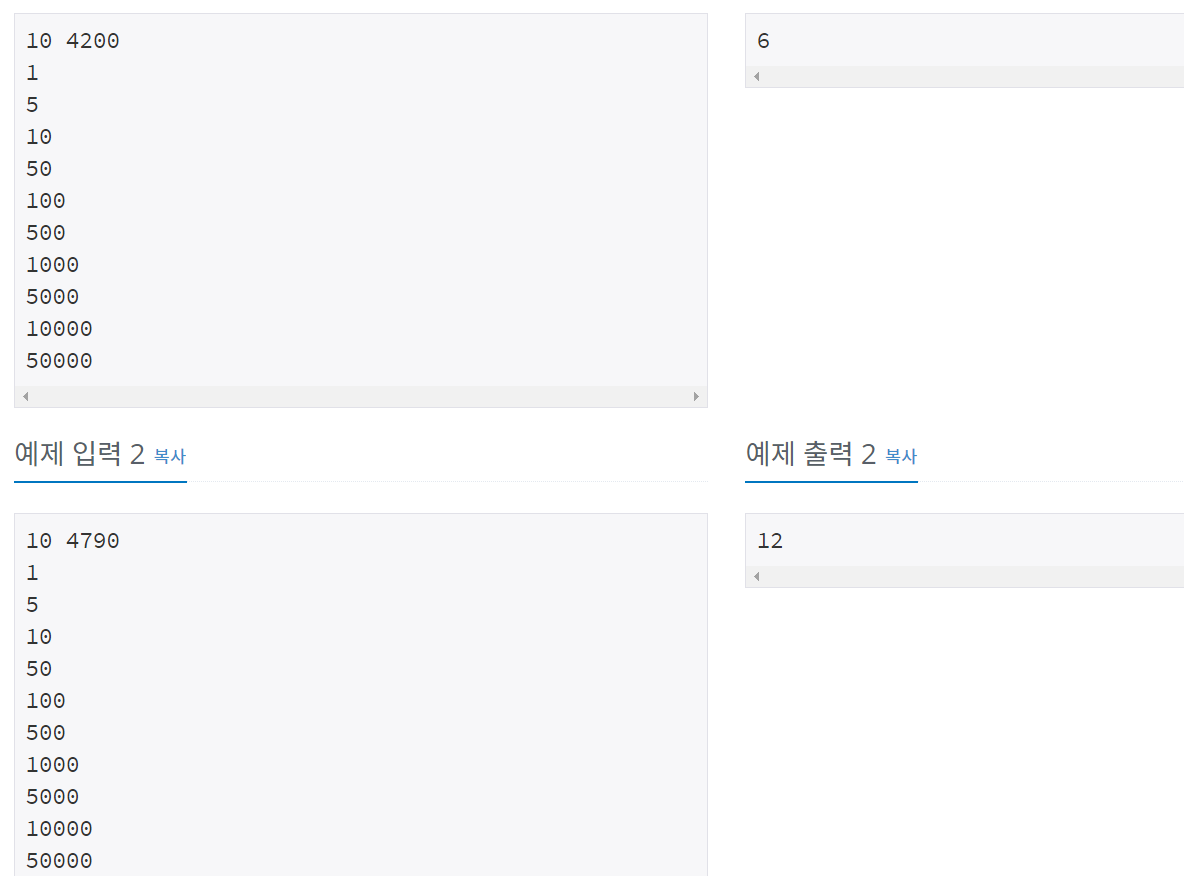
그리디 알고리즘을 통해 역순으로 입력된 coin 배열을 확인하면서 원하는 K원에 맞추어 필요한 동전을 계산해준다. 그 상황에서 최대로 고를 수 있는 동전갯수를 계산하는 알고리즘을 사용한다. 예를 들어, 4200원에 도달하기 위해 1000원에서 최대 4개를 선택해주어야하고, 남은 200을 위해 100원을 최대 2개를 선택해야한다.
#include <iostream>
using namespace std;
int main() {
int N, K;
cin >> N >> K;
int coin[10];
for (int i = 0; i < N; i++)
cin >> coin[i];
int count = 0;
for (int i = N - 1; i >= 0; i--) {
if (K == 0)
break;
if (coin[i] <= K) {
count += K / coin[i];
K -= K / coin[i] * coin[i];
}
}
cout << count;
}