종이 시험지 자동 채점 프로그램 시리즈

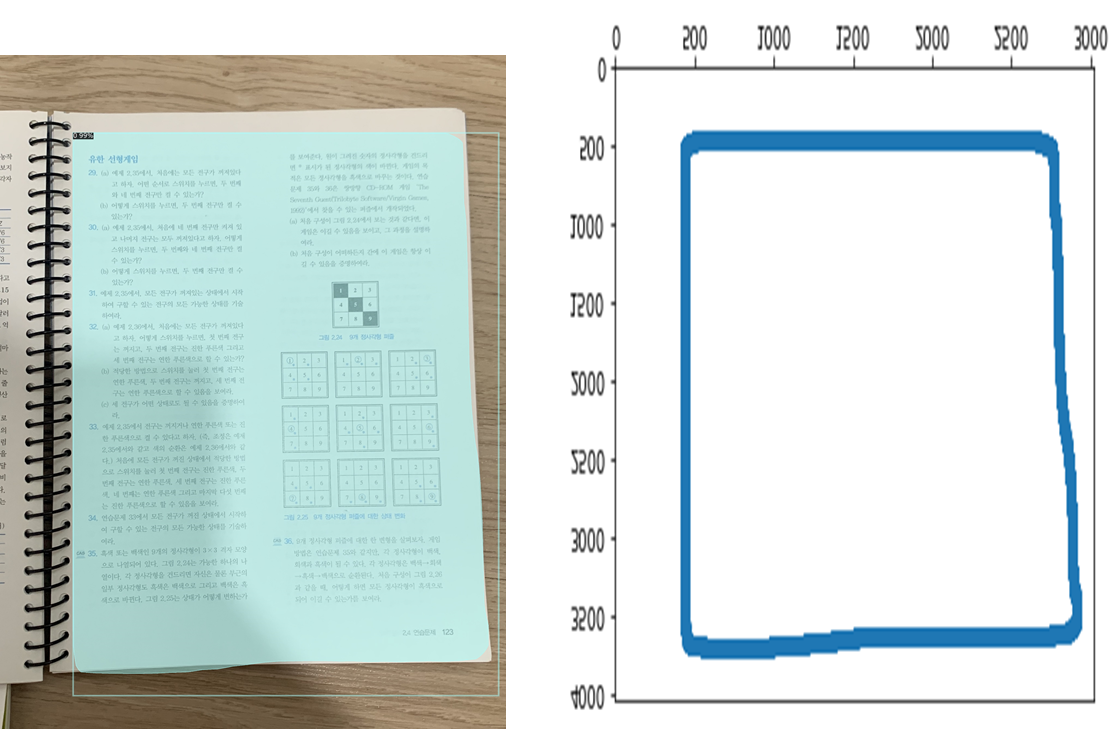
마스크 이미지로 부터의 가장자리

ch2에서 다루었던 segmentation 후 또다른 처리를 진행하기로 했습니다. 많이 기울어진 사진에 대해 투시변화를 통해 펼쳐주는 작업을 진행해 정확도를 높이기로 했습니다.

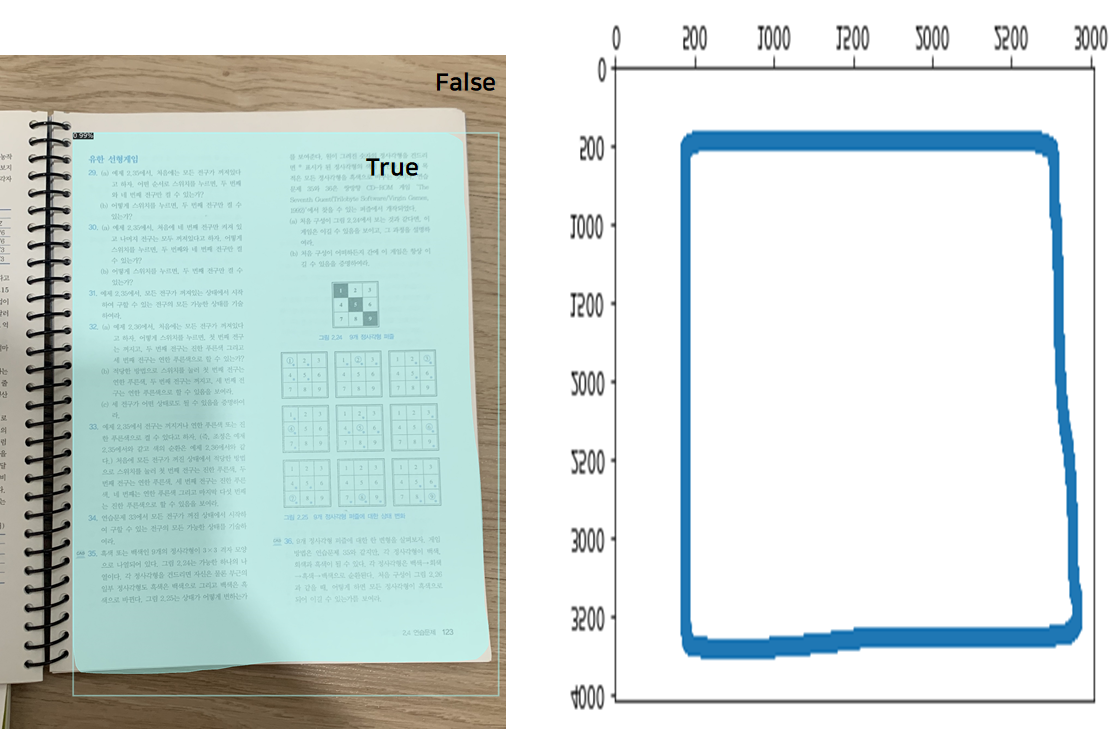
먼저 위의 이미지에서 왼쪽 이미지는 segmentation 결과 나타나는 출력 이미지 입니다. 여기서 마스크 행렬을 얻을 수 있고 마스크 범위안은 True, 범위 밖 즉 배경으로 인식한 부분은 False 값으로 저장되어 있습니다. 여기서 마스크 범위 가장자리의 종이의 변에 해당하는 부분을 따로 점을 찍어 표현한 것이 오른쪽 입니다. 이제 여기서 각 네변의 직선의 방정식을 구하기 위해 위, 왼쪽, 오른쪽, 아래 총 네 범위로 나누어 점들을 각각 저장해야 합니다.

각 변의 점의 좌표

마지막에 깃허브를 통해 제가 작성한 코드를 전체 공개할 예정이며, 여기서 사용한 코드를 일부 보여드립니다.

## 가장자리 true 값 좌표 알기 / A, B 행렬에 넣기
from matplotlib import pyplot as plt
import numpy as np

upA = np.empty((0,2), int)
upB = np.array([])
rightA = np.empty((0,2), int)
rightB = np.array([])
leftA = np.empty((0,2), int)
leftB = np.array([])
downA = np.empty((0,2), int)
downB = np.array([])

## scatter를 위한 list
#uplistx = []
#uplisty = []
#rightlistx = []
#rightlisty = []
#leftlistx = []
#leftlisty = []
#downlistx = []
#downlisty = [] 
#totalx = []
#totaly = []

for i in range(0, pred_masks.size()[1],2):
  for j in range(0, pred_masks.size()[2],2):
    if(pred_masks[0][i][j] == True):

      if (pred_masks[0][i-1][j] == False and pred_masks[0][i+1][j] == True):
        if(len(upA) == 0 or upA[-1][0] == j):
          upA = np.append(upA, np.array([[j, 1]]), axis=0)
          upB = np.append(upB, np.array([i]))
          #uplistx.append(j)
          #uplisty.append(i)
          #totalx.append(j)
          #totaly.append(i)
          continue

        if(abs((upB[-1] - i) / (upA[-1][0] - j)) < 3):
          upA = np.append(upA, np.array([[j, 1]]), axis=0)
          upB = np.append(upB, np.array([i]))
          #uplistx.append(j)
          #uplisty.append(i)
          #totalx.append(j)
          #totaly.append(i)

          if(len(upA) == 1):
            upA.pop(0)
            upB.pop(0)


      elif (pred_masks[0][i][j+1] == False and pred_masks[0][i][j-1] == True):
        if(len(rightA) == 0 or rightA[-1][0] == j):
          rightA = np.append(rightA, np.array([[j, 1]]), axis=0)
          rightB = np.append(rightB, np.array([i]))
          #rightlistx.append(j)
          #rightlisty.append(i)
          #totalx.append(j)
          #totaly.append(i)
          continue

        if(abs((rightB[-1] - i )/ (rightA[-1][0] - j)) > 6):
          rightA = np.append(rightA, np.array([[j, 1]]), axis=0)
          rightB = np.append(rightB, np.array([i]))
          #rightlistx.append(j)
          #rightlisty.append(i)
          #totalx.append(j)
          #totaly.append(i)
          
          if(len(rightA) == 1):
            rightA.pop(0)
            rightB.pop(0)
        

      elif (pred_masks[0][i][j-1] == False and pred_masks[0][i][j+1] == True):
        if(len(leftA) == 0 or leftA[-1][0] == j):
          leftA = np.append(leftA, np.array([[j, 1]]), axis=0)
          leftB = np.append(leftB, np.array([i]))
          #leftlistx.append(j)
          #leftlisty.append(i)
          #totalx.append(j)
          #totaly.append(i)
          continue
          
        if(abs((leftB[-1] - i )/ (leftA[-1][0] - j)) > 6):
          leftA = np.append(leftA, np.array([[j, 1]]), axis=0)
          leftB = np.append(leftB, np.array([i]))
          #leftlistx.append(j)
          #leftlisty.append(i)
          #totalx.append(j)
          #totaly.append(i)

          if (len(leftA) == 1):
            leftA.pop(0)
            leftB.pop(0)


      elif (pred_masks[0][i+1][j] == False and pred_masks[0][i-1][j] == True):
        if(len(downB) == 0 or downA[-1][0] == j):
          downA = np.append(downA, np.array([[j, 1]]), axis=0)
          downB = np.append(downB, np.array([i]))
          #downlistx.append(j)
          #downlisty.append(i)
          #totalx.append(j)
          #totaly.append(i)

          continue
        if(abs((downB[-1] - i )/ (downA[-1][0] - j)) < 3):
          downA = np.append(downA, np.array([[j, 1]]), axis=0)
          downB = np.append(downB, np.array([i]))
          #downlistx.append(j)
          #downlisty.append(i)
          #totalx.append(j)
          #totaly.append(i)

          if(len(downA) == 1):
            downA.pop(0)
            downB.pop(0)

주석처리 되어 있는 부분은 시각화를 위한 리스트 append 작업이며, 시각화를 원하지 않을 때는 주석처리를 해두어 시간을 절약했습니다.

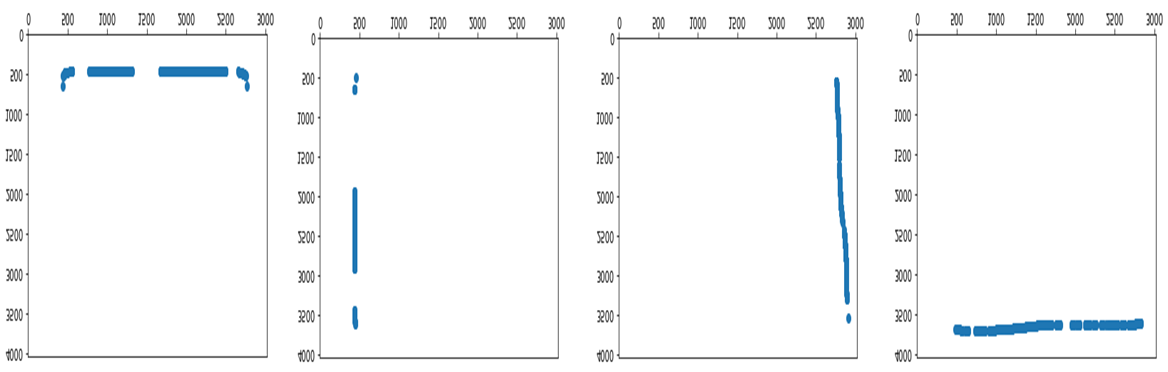
시각화 하게 되면 각 변에 대해 점들이 위와 같이 찍히게 됩니다. 이것을 이미지 픽셀의 x좌표에 대한 직선의 방정식으로 표현해야 합니다.

기울기와 y절편구하기

이때 사용한 것은 선형대수의 최소제곱법 입니다.

먼저 x값들에 대한 y값을 표현한 선형식들이 도출됩니다.

그것을 AX = B라는 식으로 표현할 수 있게 되고, 여기서 X행렬은 기울기와 y절편이 포함된 행렬입니다. 그 후 양변에 𝐴^𝑇를 곱하여, 좌변에 X만을 남겨 정리하면 아래와 같은 식이 도출됩니다.

X = (𝑨^𝑻 𝑨)^(−𝟏) 𝑨^𝑻B

이것을 numpy에서 제공하는 linalg의 역행렬과 곱행렬을 계산하는 inv, dot함수를 통해 각 변에 대해 계산을 해주었습니다.

import numpy.linalg as lin

X_up = np.linalg.inv(upA.T.dot(upA)).dot(upA.T).dot(upB)
X_right = np.linalg.inv(rightA.T.dot(rightA)).dot(rightA.T).dot(rightB)
X_left = np.linalg.inv(leftA.T.dot(leftA)).dot(leftA.T).dot(leftB)
X_down = np.linalg.inv(downA.T.dot(downA)).dot(downA.T).dot(downB)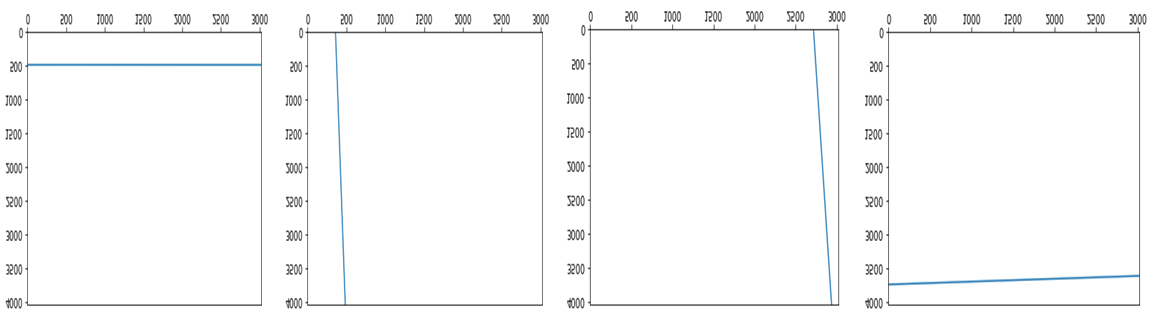

구한 기울기와 y좌표를 통해 그래프를 plot하면 위와 같은 그래프를 각각 얻을 수 있고, 이제 이 네개의 직선에 대한 교점을 구해 투시변화를 위한 네 꼭지점을 구하면 됩니다.

교점, 네 꼭지점 구하기

교점을 구하기 위해서는 겹쳐지는, 교점이 발생하는 두 직선의 방정식을 연립하여 풀어주면 교점의 x좌표와 y좌표를 구할 수 있습니다.

여기서는 이러한 연립방정식을 해결하는 numpy의 linalg solve함수가 있어 이것을 사용하여 해결해 주었습니다.

위 그림처럼 각 교점에 대해 solve함수로 모두 구해주었고, 가끔 교점의 좌표가 이미지 픽셀 범위를 벗어나는 경우가 있어, 이 경우에는 0이나 픽셀의 최대값으로 설정해주는 작업을 추가로 진행하였습니다.

PerspectiveTransform 투시변환

이제 마지막 단계입니다. 앞에서 구한 네개의 꼭지점, 변환해야할 네 좌표점과, 출력될 이미지의 끝 좌표점을 입력하여 getPerspectiveTransform 함수를 통해 투시변환을 진행해주면 됩니다.

from PIL import Image

pts1 = np.float32([itpoint_1, itpoint_2, itpoint_4, itpoint_3])

w1 = abs(itpoint_1[0] - itpoint_2[0])
w2 = abs(itpoint_3[0] - itpoint_4[0])
h1 = abs(itpoint_1[1] - itpoint_3[1])
h2 = abs(itpoint_2[1] - itpoint_4[1])
width = max([w1, w2])
height = max([h1, h2])

pts2 = np.float32([[0,0], [width-1, 0], [width-1, height-1], [0, height-1]])

mtrx = cv2.getPerspectiveTransform(pts1, pts2)

result = cv2.warpPerspective(im, mtrx, (int(width), int(height)))
plt.imshow(result)

그 결과는 위 이미지와 같이 도출됩니다.

조금더 큰 효과를 테스트 해보기 위해 아래의 사진을 처리해보았습니다.

그 결과는 확실히 기울어진 문제가 조금더 정면으로 변환된 것을 확인할 수 있었고, chapter2에서 진행했던 segmentation 모델에 기울어진 시험지 이미지를 좀더 추가해 학습을 진행한다면 더 좋은 성능을 가질 거라고 생각합니다. 그래서 추후에 이미지를 추가해 학습을 진행할 예정입니다.

감사합니다.

모든 코드는 깃허브에 있습니다.

🎁 Paper Perspective Transform With LSM and Segmentation