[딥러닝] 역전파 알고리즘 (Backpropagation)

경사 하강법의 문제

• 손실함수에 경사 하강법 적용 시, 신경망의 역방향으로 미분값을 순차로 곱해야 한다는 점
• 모든 가중치 파라미터에 대해 개별적으로 적용 시 같은 미분값이 반복 계산된다는 점 -> 비효율적 !
  
  

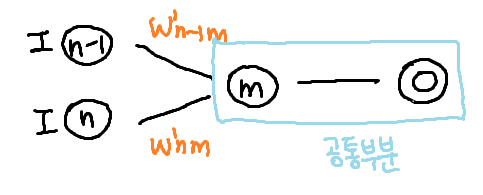
-> 그렇다면 중복되는 편미분 값들 저장해놨다가 필요할 때 꺼내 써보자. (역전파의 두등등장 😎)

---

역전파 알고리즘이란 ?

• 현재 파라미터를 통한 신경망의 결과 값을 다시 역으로 입력 방향으로 보내며 가중치를 재업데이트하는 과정
• 즉, 결과의 에러 (Error)에 영향을 미친 노드를 파악하고 줄여 나가는 방식
• 딥러닝 모델을 훈련시키는 가장 대표적인 방법

---

실행 순서

1. 손실함수 미분

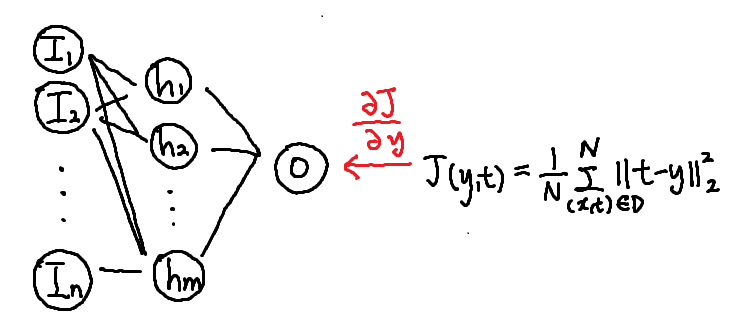
1 ) 손실 함수 미분

• 손실 함수 $J(y)$의 미분인 $\frac{∂J}{∂y}$ 를 계산한다.

2 ) 출력 뉴런에 미분 전달

• 계산된 값을 출력 계층인 $O$에 전달한다.

2. 출력 뉴런 미분

출력 뉴런 $O$는 미분 값 $\frac{∂J}{∂y}$ 를 전달 받고 가중치의 미분을 계산해서 가중치를 업데이트하고, 입력의 미분을 계산해서 은닉 계층에 전달한다.

또한 $O$는 활성 함수 $y$ = $Identitiy(z^2)$ 와 가중 합산인 $z^2$ = $w_1^2*a_1^1 + w_2^2*a_2^1 + ... + w_m^2*a_m^1$ 으로 이루어지므로 미분을 별도로 수행해줘야 한다.

1) 공통 부분 계산

• 활성 함수 $y$ = $Identitiy(z^2)$ 의 미분인 $\frac{∂y}{∂z^2}$ 과 $\frac{∂J}{∂y}$ 를 곱한 $\frac{∂J}{∂z^2}$ 가 공통 부분이 된다.

2) 가중치 업데이트

• $\frac{∂z^2}{∂w_1^2}, ... , \frac{∂z^2}{∂w_m^2}$ 를 각각 계산한 후 공통 부분인 $\frac{∂J}{∂z^2}$ 를 곱해준다.

• $\frac{∂J}{∂w_1^2}, ..., \frac{∂J}{∂w_m^2}$ 를 통해 $w_1^2, ..., w_m^2$ 를 업데이트한다.

3) 은닉 계층에 미분 전달

• $\frac{∂z^2}{∂a_1^1}, ... , \frac{∂z^2}{∂a_m^1}$ 를 각각 계산한 후 공통 부분인 $\frac{∂J}{∂z^2}$ 를 곱해준다.

• $\frac{∂J}{∂a_1^1}, ..., \frac{∂J}{∂a_m^1}$ 를 각 은닉 뉴런에 전달한다.

3. 은닉 뉴런 미분

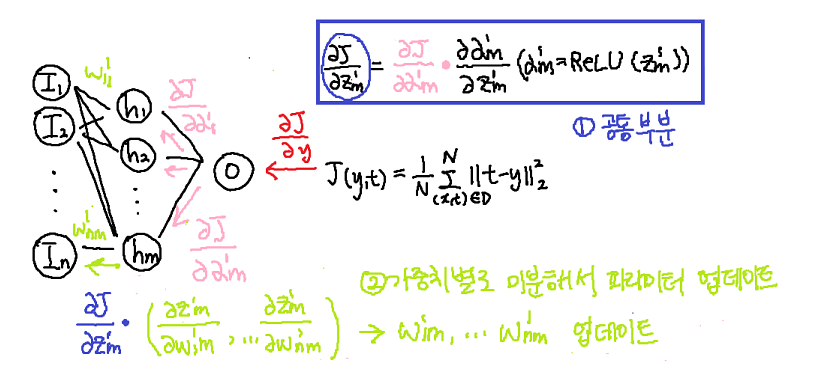
1) 공퉁 부분 계산

• 활성 함수 $a_m^1$ = $ReLU(z_m^1)$ 의 미분인 $\frac{∂a_m^1}{∂z_m^1}$ 과 $\frac{∂J}{∂a_m^1}$ 을 곱한 $\frac{∂J}{∂z_m^1}$ 가 공통 부분이 된다.

2) 가중치 업데이트

• $\frac{∂z_m^1}{∂w_1m^1}, ... , \frac{∂z_m^1}{∂w_nm^1}$ 를 각각 계산한 후 공통 부분인 $\frac{∂J}{∂z_m^1}$ 를 곱해준다.

• $\frac{∂J}{∂w_1m^1}, ..., \frac{∂J}{∂w_nm^1}$ 를 통해 $w_1m^1, ..., w_nm^1$ 를 업데이트한다.

3) 입력 계층에 미분 전달

• 입력 계층에는 가중치가 없기 때문에 미분 값을 전달하지 않아도 된다.

---

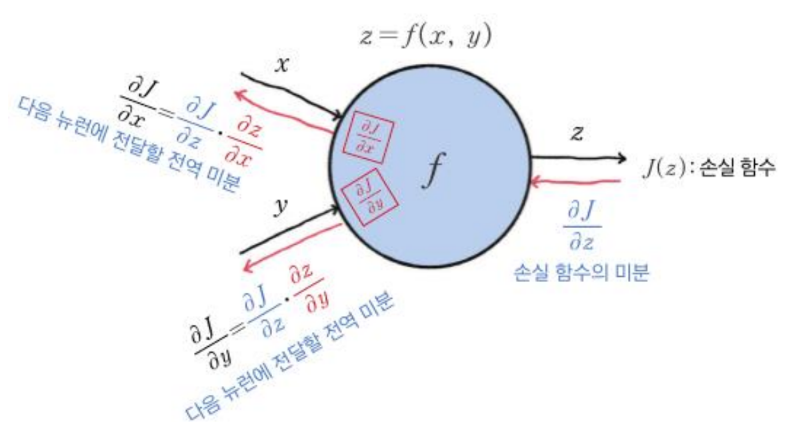
뉴런 관점에서 보는 역전파

각 뉴런 입장에서는 연관된 가중치에 대한 지역적 미분값만을 구하고 전달받은 (공통) 미분값을 곱한다.

연쇄 법칙을 통해 가중치에 대한 손실함수의 미분을 구하고 경사 하강법을 적용한다.

-> 가중치 업데이트

---

🌟 요약

경사 하강법에서 모든 가중치 파라미터에 대해 공통적으로 연산되는 부분의 반복으로 인한 계산의 비효율성이라는 문제를 해결하기 위해 역전파 두등등장.

공통된 부분은 저장해놨다가 꺼내서 쓰지만, 공통되지 않은 부분은 미분해서 그 파라미터를 업데이트 --> 역방향으로 이 과정의 반복을 통해 결과의 에러 최소화 !