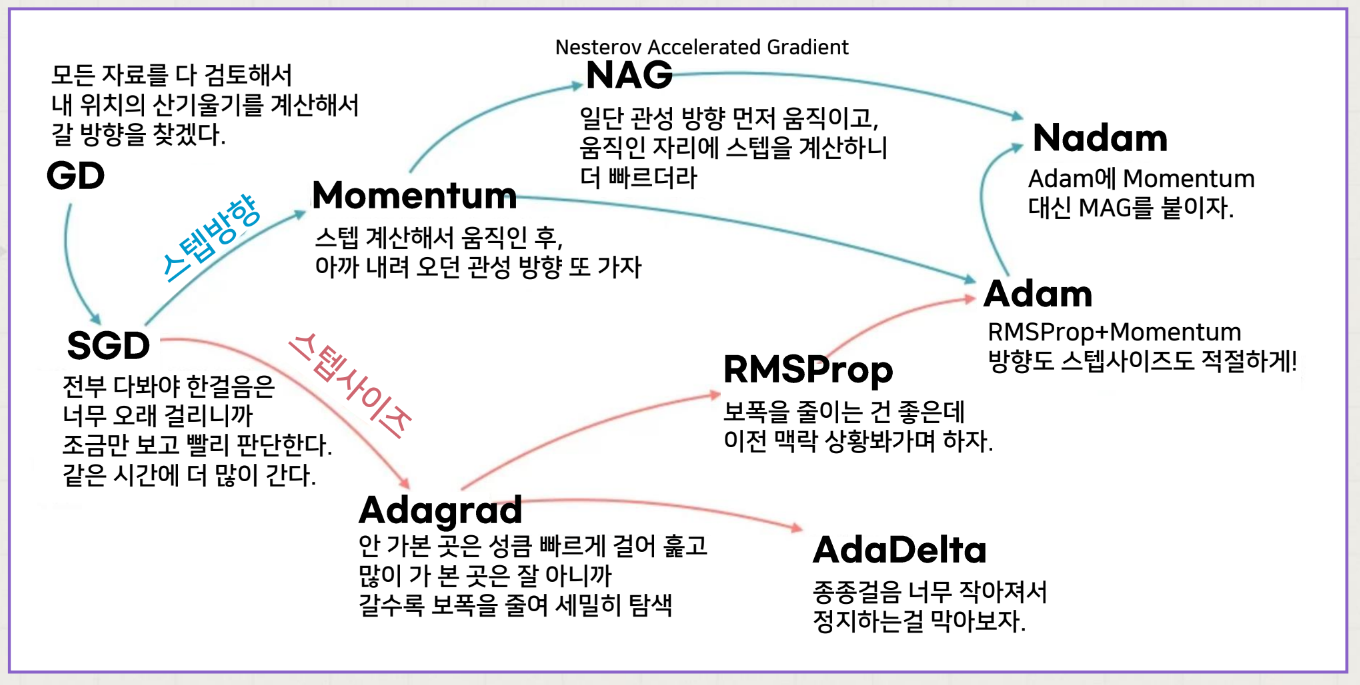
최적화 알고리즘의 개요
⚠️ 확률적 경사 하강법의 문제점
1. 고정된 학습률 활용 -> 최적해에 수렴하지 않을 수 있음.
-> 적응적 학습률 활용 !
2. 1차 미분인 기울기만 사용 -> 특정 차원에 의존적일 수 있음.
-> 2차 미분 활용 !
3. 안장점 (임계점이지만 극값을 가지지 않는 점)
-> 이전 업데이트를 고려한 모멘텀(Momentum) 활용 !
Momentum
목적함수 의 최소 지점을 찾기 위해 경사 하강법에서 (1차) 미분값에 속도를 통한 관성 효과를 반영해 학습한 것이다.
즉, 가중치를 수정하기 전에 이전 수정 방향 (+, -) 을 참고하여 같은 방향으로 일정한 비율만 수정하게 된다.
이로 인해 지그재그 현상이 줄어들고, 이전 이동 값을 고려하여 일정 비율만큼 다음 값을 결정하므로 관성 효과를 얻을 수 있다.

-
일 때는, 경사가 가파른 곳에서 빠르게 이동하고 안장점 혹은 지역적 최소 지점을 벗어나기에 유리하다.
-
일 때는, 경사 하강법과 동일하다.
⚠️ 오버슈팅 (Overshooting) 문제
그러나 최소 지점 주변의 경사가 가파른 경우, 관성에 의해 최소 지점을 지나칠 우려가 있을 수 있다.
Nesterov Momentum
위에서 Momentum 의 오버슈팅 문제를 해결하기 위해 한 걸음 미리 갔을 때의 미분값을 반영하여 학습하는 것이다.
이는 모멘텀으로 절반 정도 이동한 후 어떤 방식으로 이동해야 하는지 다시 계산하여 결정한다.
따라서 모멘텀 방법의 이점인 빠른 이동 속도는 그대로 가져가면서 멈추어야 할 적절한 시점에서 제동을 거는 데 훨씬 용이하다.

AdaGrad
목적함수 의 곡면의 변화량에 따라 적응적 (Adaptive) 으로 학습률을 결정하는 알고리즘이다.
곡면의 변화량이 크면 적은 폭으로, 작으면 큰 폭으로 이동한다.
즉, 많이 변화한 변수는 최적 값에 근접했을 것이라는 가정하에 작은 크기로 이동하면서 세밀하게 값을 조정하고, 반대로 적게 변화한 변수들은 학습률을 크게 하여 빠르게 오차 값을 줄이고자 하는 것이다.
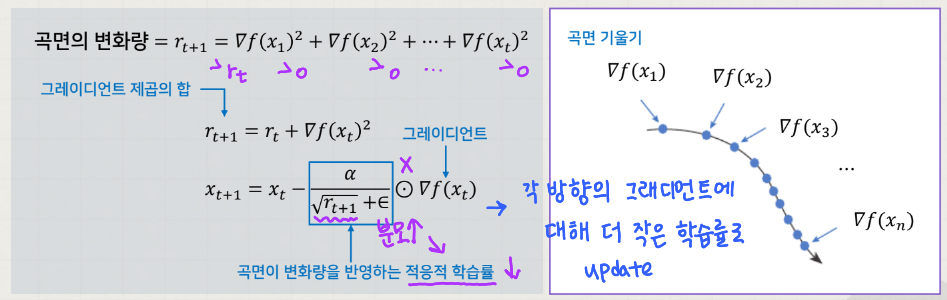
⚠️ 조기 중단 (early stopping) 문제
오버슈팅과 비슷한 개념으로, 경사가 가까운 지점에서 시작하면 초반에 학습률이 급감하여 조기 중단될 수 있다.
RMSProp
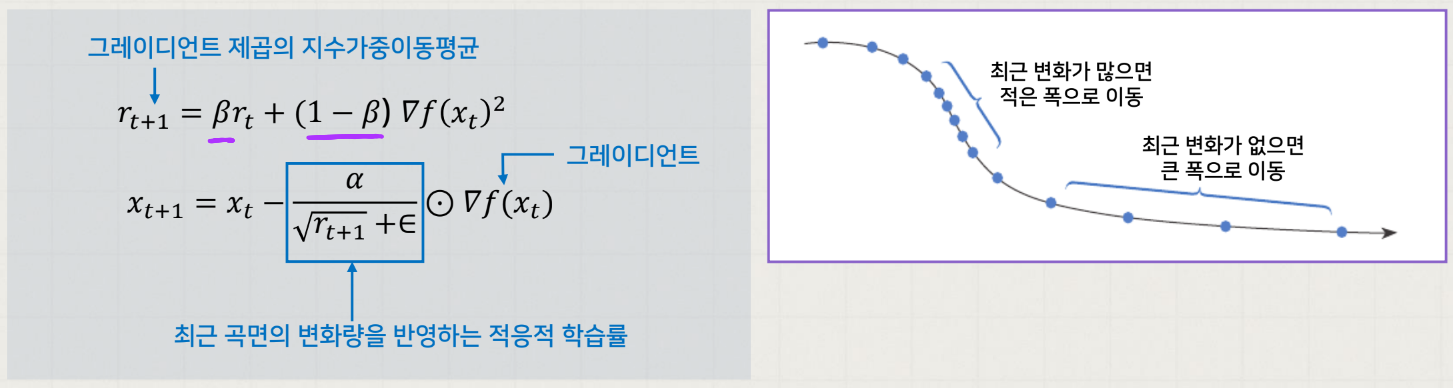
위에서 AdaGrad 의 조기 중단 문제를 해결하기 위해 가중이동평균을 적용해 적응적 학습률을 결정하는 알고리즘이다.
최근 변화는 많이 반영되고, 오래된 변화는 적게 반영되게 할 수 있다.
Adam
위에서 설명한 RMSProp (곡면의 변화량에 따른 적응적 학습률) 에 Momentum (관성 효과) 을 추가 적용한 것이다.
가장 많이 쓰이는 효과적인 방법이다. 😊

한눈에 요약