LeetCode 1 Two Sum

nayu1105·2023년 8월 30일

leetcode 알고리즘

LeetCode

목록 보기

18/28

LeetCode 1 Two Sum 풀러가기

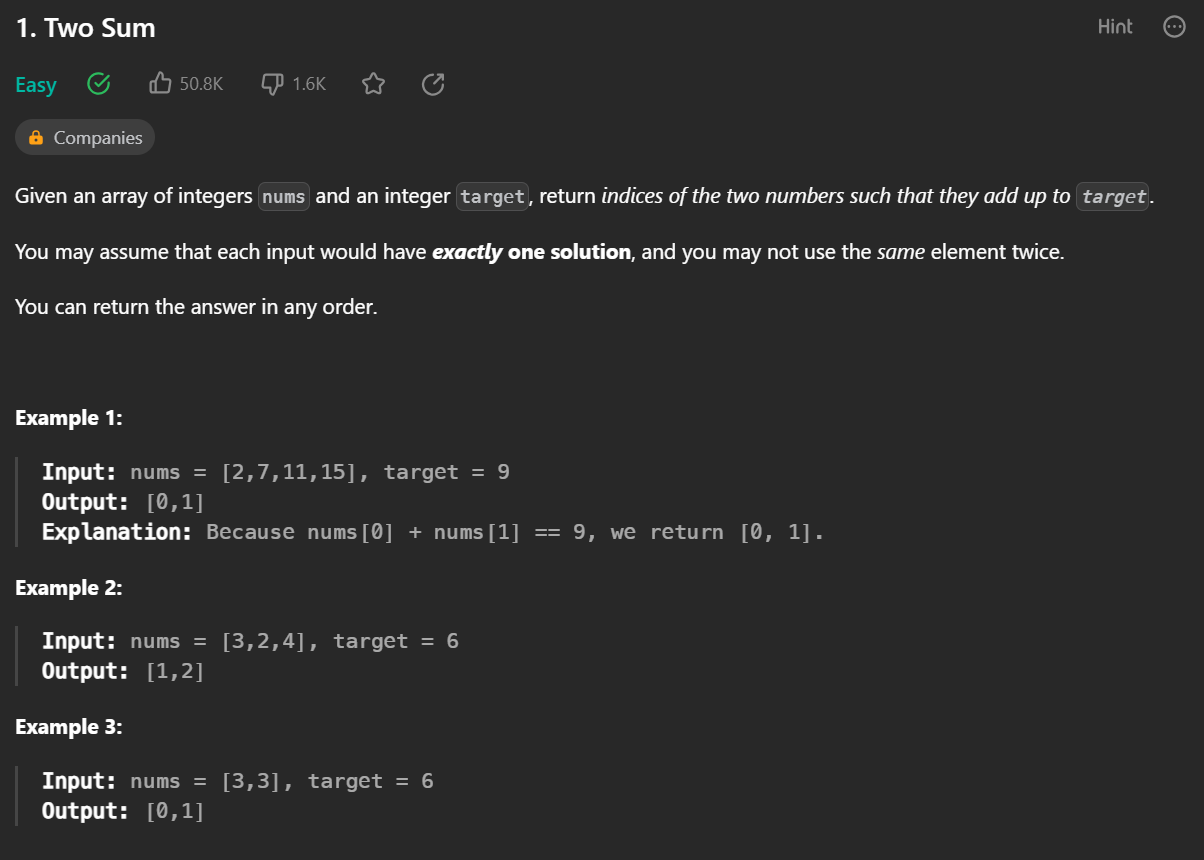
문제

문제 분석

첫번째 시도

가장 빠르게 생각난 방법은 이중 포문을 써서 모든 경우의 수를 조사하는 것이였다.

대신 이 방법은 시간복잡도가 O(N^2) 이였다.

코드

class Solution {
    public int[] twoSum(int[] nums, int target) {
        for(int i=0; i<nums.length; i++){
            for(int j=i+1; j<nums.length; j++){
                if(nums[i] + nums[j] == target)return new int[] {i, j};
            }
        }

        return new int[2];
    }
}

결과 : 성공

Runtime

Memory

역시나 시간이 너무 오래걸리는 방법이였다. 시간을 줄이기 위해 다른 방법을 고민해보았다.

다른 분의 코드(시간 개선)

sort하고, 투포인터를 활용해서 이분탐색을 해야하나 고민했는데, 반례들이 자꾸 떠올라서 안 될 것 같았다.

결국, 다른 분의 코드를 참고했는데, 이것은 map을 사용한 방법이였다.

map의 key값을 nums로, value를 nums의 갯수로 저장하였다.

그리고 nums를 탐색하며 map에 taget-nums가 없다면 해당 nums를 추가하고, map에 있다면 이 두개가 정답인 한 쌍이라는 것이기에 반환하면 됐다.

코드는 아래와 같다.

코드

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> numMap = new HashMap<>();
        int n = nums.length;

        for (int i = 0; i < n; i++) {
            int complement = target - nums[i];
            if (numMap.containsKey(complement)) {
                return new int[]{numMap.get(complement), i};
            }
            numMap.put(nums[i], i);
        }

        return new int[]{}; 
    }
}