Abstract

DDPM achieved great performance in image generation, yet require many steps of Markov chain to produce a sample. The process is very slow compared to the previous GAN approach. A more efficient way to sample will accelerate the whole process of DDPMs in the mean time keeping the training procedure same, namely DDIM. We generalize the DDPM process into non-Markovian diffusion process using the same training objective. The non-markovian process can correspond to generative process that is deterministic, giving rise to implicit models that produce high quality samples faster. DDIM achieves semantically meaningful image interpolation directly in the latent space and reconstructs observations very precisely.

Deterministic Process: In DDIM, the generative process is designed to be deterministic, meaning that given a specific initial noise, the sequence of steps taken to generate a sample is fixed and does not involve any randomness.
Reconstruct Observation well: DDIM is highly effective at generating samples that closely match the original data used during training. This low error is achieved through the deterministic and flexible nature of the reverse process in DDIM,

Introduction

Existing Models in Generative models

GAN	DDPM & NCSN
Better sample quality than VAE, Flow	Great sample quality without adverserial training
Very hard to optimize because training is very unstable	Many denoising autoencoding models trained to denoise samples corrupted by various levels of Gaussian noise.
Mode collase issue(limited modes)	Require many iterations to produce a high quality sample

DDIM

To meet the efficiency gap between GAN and DDPM, authors present DDIM. DDIM is a implicit model like GAN highy related to DDPM, in that they share the same Training Objective. By generalizing the forward(diffusion) process to non-Markovian process, it is possible to design a training objective which it happens to be exactly same as DDPM objective. The advantage of non-Markovian process is the possibility of choosing a large variety of Generative models that use the same neural network simply by choosing a different pair of (non-Markovian diffusion process, reverse Markovian generative process). By using non-Markovian diffusion process, it is feasible to achieve a shorter reverse generative Markov chain.(-> Advantage of non-markovian process)

The benefits of DDIM over DDPM is as follows

• Sample generation quality is superior to DDPM in 10X ~ 100X accelerated sampling
• Consistency property is better held : Starting from the same latent variable, samples with different chain lengths
• Consistency in the DDIM allows semantically meaningful image interpolation via manipulating the initial latent variables.

Background

The parame- ters θ are learned to fit the data distribution q(x0) by maximizing a variational lower bound:

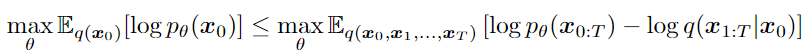
Variantional Inference for Non-Markovian Forward Process

Our observation of DDPM objective in the form of $L_\gamma$ is that it only depends on the marginal distribution $q(x_t|x_0)$ but not directly on the joint distribution $q(x_{1:T}|x_0)$.
Explanation

1. Dependency on Marginal Distribution:

• The DDPM objective focuses on how well the model can predict each noisy data point $𝑥_t$ given the original data $x_0$.
• This means that at each time step t, the objective is concerned with $𝑞(𝑥_𝑡∣𝑥_0)$, which summarizes the effect of noise added up to that step.

2. Not Directly on the Joint Distribution:

• The joint distribution $q(x_{1:T}|x_0)$ captures the entire sequence of noisy data points, but DDPM objective doesn't require modeling the correlation between all these points directly.
• Instead, by focusing on the marginals, the model can simplify the training objective and avoid the complexity of dealing with the full joint distribution.

By depending only on the marginals, the DDPM objective simplifies the learning process. The model needs to learn how to handle the noise at each step without explicitly considering the dependencies between all steps.

Non-Markovian Forward Processes

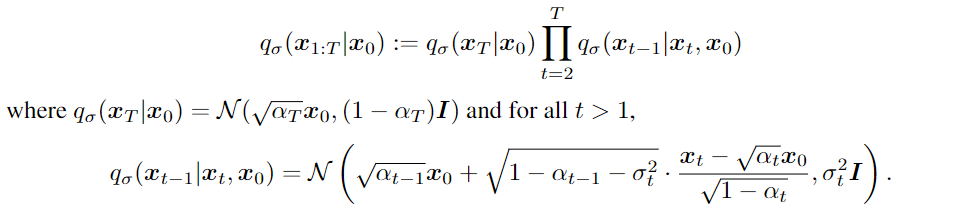
The mean function is chosen in order to satisfy the condition $q_\sigma(x_t|x_0)=\mathcal{N}(\sqrt{\alpha_t}x_0,(1-\alpha_t)I)$ for all t, so that it defines a joint inference distribution that matches the Marginal. Since each $x_t$ could depend on both $x_{t−1}$ and $x_0$. The magnitude of σ controls the how stochastic the forward process is; when σ → 0 of no stochasticity, we reach an extreme case where as long as we observe $x_0$ and $x_t$ for some t, then $x_{t−1}$ become known and fixed.

Proven that Markov forward process $q$ and non-Markovian forward process $q_\sigma$ has the same Margin

Generative Processes and unified variational inference objective

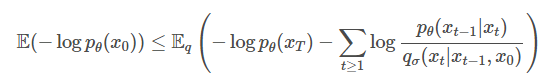
Above is a variational lower bound of the DDIM, only difference with DDPM is the non-Markovian forward process $q_\sigma$. The loss can be derived the equivalent way as DDPM resulting in:

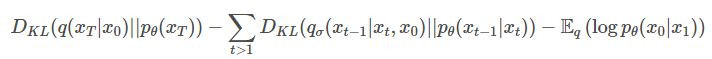
Similarly the first term is not of interest and organizing the equation respect to reverse process $p_\theta$:

The term $x_0(x_t,\epsilon_\theta)$ is derived from the equation $x_0=(x_t - \sqrt{1-\bar{\alpha}_t}\space.\space\epsilon_\theta^{(t)}(x_t))/\sqrt{\bar{\alpha}_t}$. Substituting p with q:

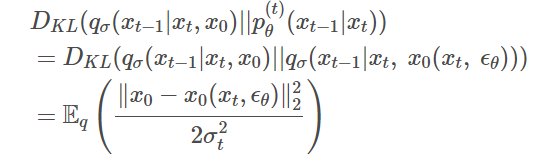
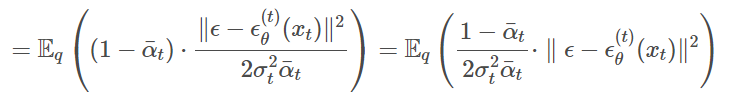
Sampling from generalized generative processes

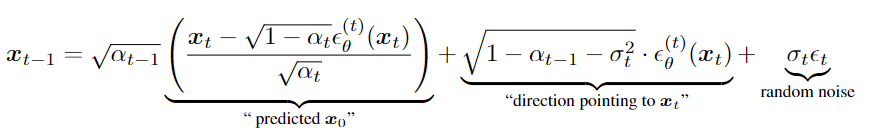
Looking at the equation, the first term depicts a process of predicting $x_0$ by removing predicted noise and scaling it by a value ($\sqrt{\frac{\alpha_{t-1}}{\alpha_t}})$ and second term adding predicted noise towards the $x_t$ direction. So in short, we are sampling from the origin $x_0$ and adding predicted noise to the origin to predict each timestep. So it is needless to predict every time and instead use only subset of the process. For time sequence $\lbrack1,2, ... T\rbrack$ and sub-sequence $\lbrack x_{\tau_1},x_{\tau_2},x_{\tau_3}...x_{\tau_s}$ we can define non-Markovian forward process $q(x_{\tau_i}|x_0) = \mathcal{N}(\sqrt{\alpha_{\tau_i}}x_0, (1-\alpha_{\tau_i})I)$. Now it doesn't depend on the previos state thus no dependency on continuos sequence.

Reference

Derivation Details : https://junia3.github.io/blog/ddim
DDIM paper : https://arxiv.org/abs/2010.02502