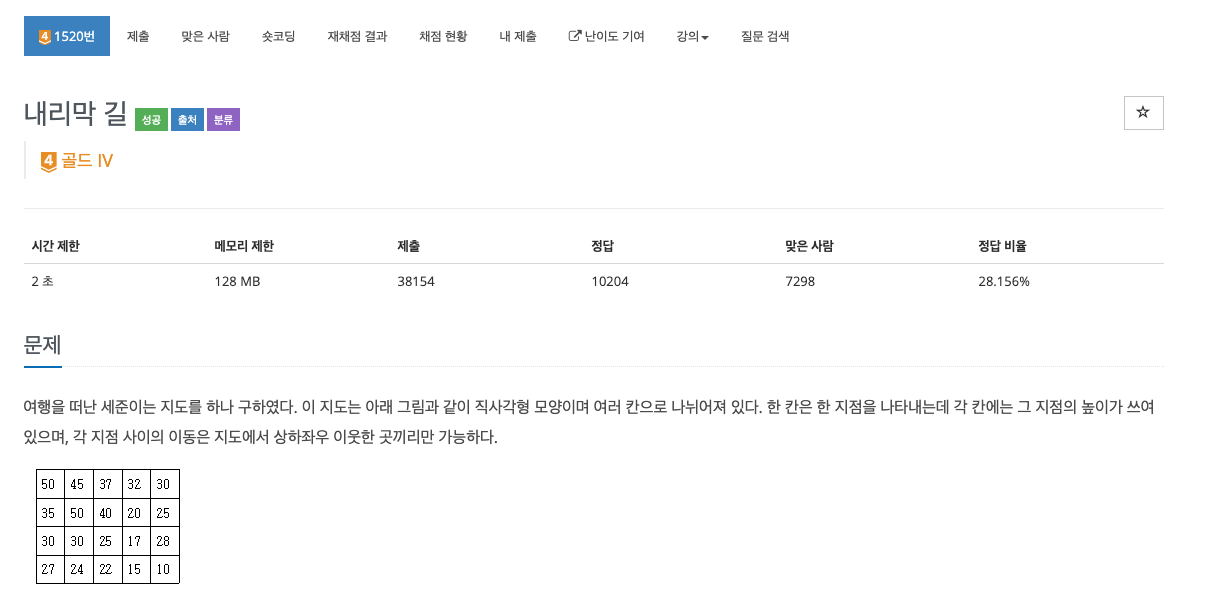
내리막길

코드

[ 시간초과 코드 ]

#include <vector>
#include <queue>
#include <iostream>
#include <cmath>
#include <algorithm>
#include <deque>
#include <numeric>
#include <map>
#include <stack>
#define ll long long
using namespace std;
int M,N,ans;
int board[550][550];
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
struct info{
    int y;
    int x;
};
stack<info> s;
// DFS든 BFS든 vis를 빼고 그냥 수행하면 된다
// -> 어차피 더 높은곳으로 이동하지 못하니까 이전 길로 돌아갈일이 없음
// 문제는 시간초과;
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> M >> N; // M=세로, N=가로
    for(int i=0;i<M;i++)
        for(int j=0;j<N;j++)
            cin >> board[i][j];
    info t = {0, 0};
    s.push(t);
    while(!s.empty())
    {
        auto cur = s.top(); s.pop();
        for(int dir=0;dir<4;dir++)
        {
            int ny = cur.y + dy[dir];
            int nx = cur.x + dx[dir];
            if(nx<0 or ny<0 or ny>=M or nx>=N) continue;
            if(board[ny][nx] >= board[cur.y][cur.x]) continue;
            if(ny == M-1 and nx == N-1) 
            {
                ans++;
                continue;
            }
            info t = {ny, nx};
            s.push(t);
        }
    }
    cout << ans;
    return 0;
}

• 원리
  • 갈 수 있는 모든 경로를 재귀 DFS라면 백트래킹을 통해서 쉽게 해결했을 것이다
  • 하지만 N과 M이 커서 재귀가 힘들다고 생각해서 stack을 이용한 DFS를 수행
    : 중요한 것은 어차피 낮은 곳으로만 이동하기 때문에 왔던 경로로는 절대 갈 수 없음
    --> BFS든 DFS든 vis[][]없이 수행만 하면 모든경로의 수를 구할 수 있음

• 문제점
  : 모든 점에 대해서 4방향을 수행하기 때문에 이론상 최대 4^(500*500)의 경우의 수로 시간초과가 발생

[ DP적용 코드 ]

#include <vector>
#include <queue>
#include <iostream>
#include <cmath>
#include <algorithm>
#include <deque>
#include <numeric>
#include <map>
#include <stack>
#define ll long long
using namespace std;
int M,N,ans;
int board[550][550];
int dp[550][550];
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
struct info{
    int y;
    int x;
};
// dp[y][x] = y,x부터 M-1 N-1까지 가는 경우의 수
int DFS(int y, int x){
    if(dp[y][x] != -1) return dp[y][x]; // dp결과가 있으면 바로 return
    if(y == M-1 and x == N-1) return 1; // 최종 목적지로 도착하면 종료
    dp[y][x] = 0;
    for(int dir=0;dir<4;dir++)
    {
        int ny = y + dy[dir];
        int nx = x + dx[dir];
        if(nx<0 or ny<0 or nx>=N or ny>=M) continue;
        if(board[ny][nx] >= board[y][x]) continue;
        // dp값이 있으면 바로 더하기
        if(dp[ny][nx] != -1){
            dp[y][x] += dp[ny][nx];
        }else{
            // dp값이 없으면 구해와서 더하기
            dp[y][x] += DFS(ny,nx);
        }
    }
    return dp[y][x];
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> M >> N; // M=세로, N=가로
    for(int i=0;i<M;i++)
        for(int j=0;j<N;j++)
        {
            cin >> board[i][j];
            dp[i][j] = -1;
        }
    ans = DFS(0,0);
    cout << ans;
    return 0;
}

• 문제 풀이
  • DFS + DP를 이용해서 이미 검증한 경로에 대해서는 중복을 생략할 수 있음
  • DP[r][c] = r행 c열에서 (M-1, N-1)로 가는 경우의 수
    (주의 : DP는 초기에 -1로 세팅 해야 한다. --> 경로의 수가 0인지 아직 구하지 않은건지 구별하기 위함)

• 느낀 점
  • 중복된 경로를 제거해야 한다는 것은 느꼈지만, 방법을 떠올리기 어려웠다
  • DFS와 DP의 조합으로 중복 경로를 제거할 수 있음을 깨달았다