전 글(Linear Regression)에서 cost function을 다뤄봤다.
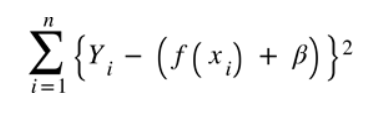
cost의 총 합을 줄이는 것이 목표인데 이때 사용하는 방법이 Gradient Descent(경사 하강법)이다.
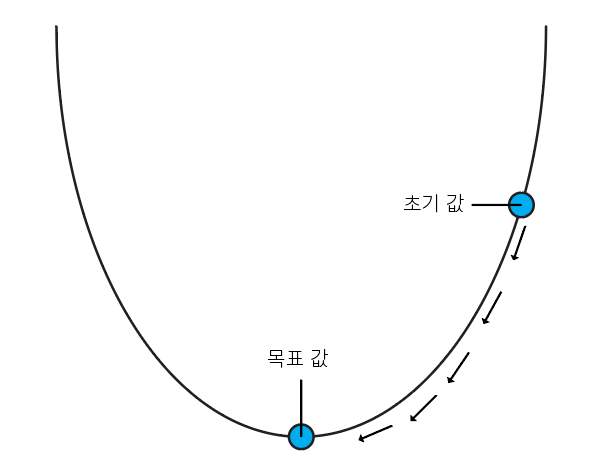
경사 하강법은 cost function을 미분하여 미분값이 낮은 최저점을 찾아가는 알고리즘이다. 위 그림처럼 기존 가중치를 경사 하강법을 통해 업데이트해가는 방식이다.(cost function은 가중치에 관한 식이기 때문에 W = weight에 관한 식을 정리한다.)
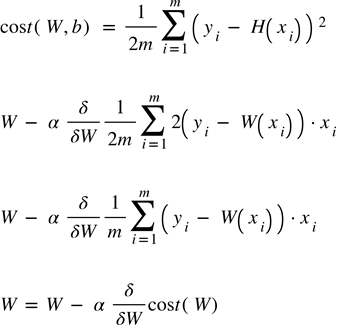
-
W,b에 관한 cost function을 위와 같이 정해놓고 (이때 2m으로 나눠주는 이유는 편미분시 제곱에 있던 2를 제거하기 위해 2m으로 나눠줬다.)
-
cost function을 편미분하여 alpha 값을 곱하여 기존 가중치에 빼준다.(이때 alpha는 보통 learning rate라고 한다.)
위 이미지에서 마지막으로 정리된 식이 weight값을 업데이트하는 방법이다.
간단한 python code를 통해 Gradient Descent를 구현해보자.
(이 코드는 tensorflow 2.7에서 작성했습니다.)
# import
import numpy as np
import tensorflow as tf
# set data
x_data = [1, 2, 3, 4]
y_data = [3, 5, 7, 9]
# y = 2x + 1을 목표로 데이터를 설정했다.
x_data = tf.cast(x_data, tf.float32)
y_data = tf.cast(y_data, tf.float32)
# set weight and bias
W = tf.Variable(tf.random.normal([1]), name="Weight")
b = tf.Variable(tf.random.normal([1]), name="Bias")
W,b
x, y, weight, bias를 정의하는 코드이다.
출력 이미지는 Weight와 Bias의 초기값을 보여준다.
epochs = 500
learning_rate = 1e-2
for epoch in range(1, epochs+1):
with tf.GradientTape() as tape:
hypothesis = W * x_data + b
cost = tf.reduce_mean(tf.square(hypothesis - y_data))
W_grad, b_grad = tape.gradient(cost, [W,b])
W.assign_sub(learning_rate * W_grad)
b.assign_sub(learning_rate * b_grad)
if epoch % 50 == 0:
print("Epochs : {:3}, cost: {:6.3f}".format(epoch, cost))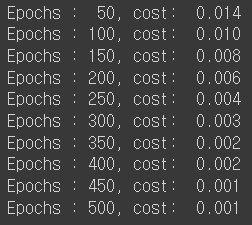
500번 동안 학습하며 가중치를 업데이트하고 출력은 50번 학습마다 cost를 출력한 것이다.
내가 원하는 가설 (hypothesis)은 y = 2x + 1 인데 w,b가 잘 학습됐는지 확인해보자.

완전 같지는 않지만 원하는 값 W : 2, b : 1에 가깝게 나온것을 확인했다.
h(x) 와 y값을 비교해보자.
for i in range(len(y_data)):
print("origin y : {} | predicted y : {}".format(y_data[i], x_data[i]*W + b))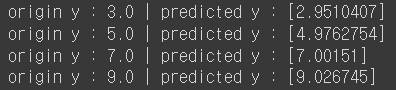
오차가 조금 있지만 원하는 가설식이 세워진 것을 확인할 수 있다.
여기까지 경사하강법과 간단한 코드로 구현하기를 진행해봤습니다. 읽어주셔서 감사합니다!
