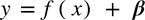Linear Regression(선형 회귀)란?
선형 회귀는 종속 변수 y와 독립 변수 x와의 선형 관계를 모델링하는 방법이다. 이때 독립 변수 x는 하나일수도, 여러 개일수도 있으며 독립 변수를 통해서 종속변수 y를 예측할 때 사용한다. 또한 독립 변수가 연속형일때는 수치예측, 범주형일때는 분류로 사용할 수 있다.
수치예측
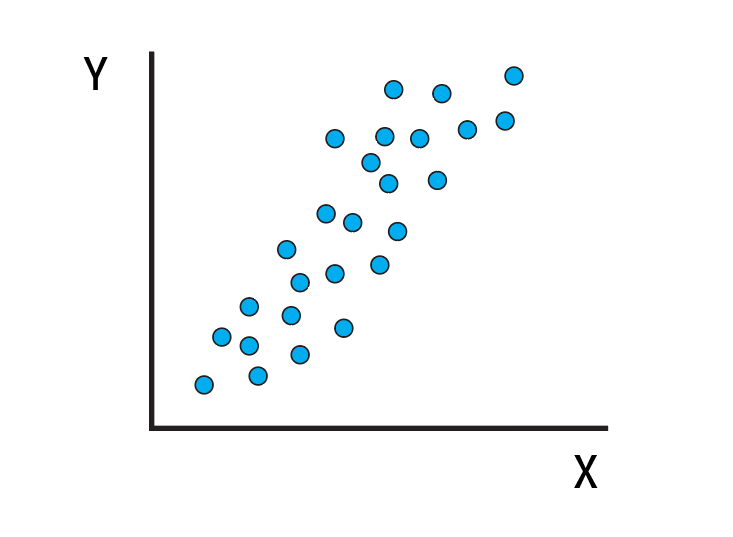
예를 들어 데이터가 위 그림처럼 분포되어 있을 때 y 값을 대표할 수 있는 하나의 선을 그어본다면 어떻게 그려볼까?
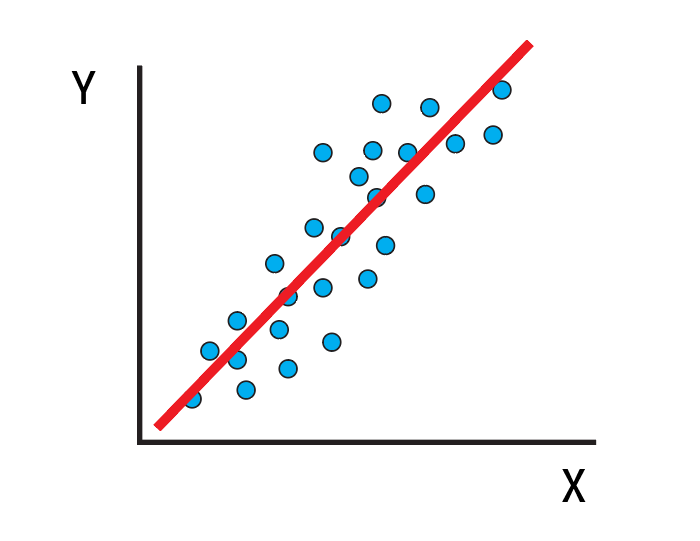
아마 이런 직선이 y 값을 대표할 수 있는 직선일 것이다.
그러고 이런 직선을 통해 우리는 새로운 x값이 들어와도 y값을 예측할 수 있을 것이다.
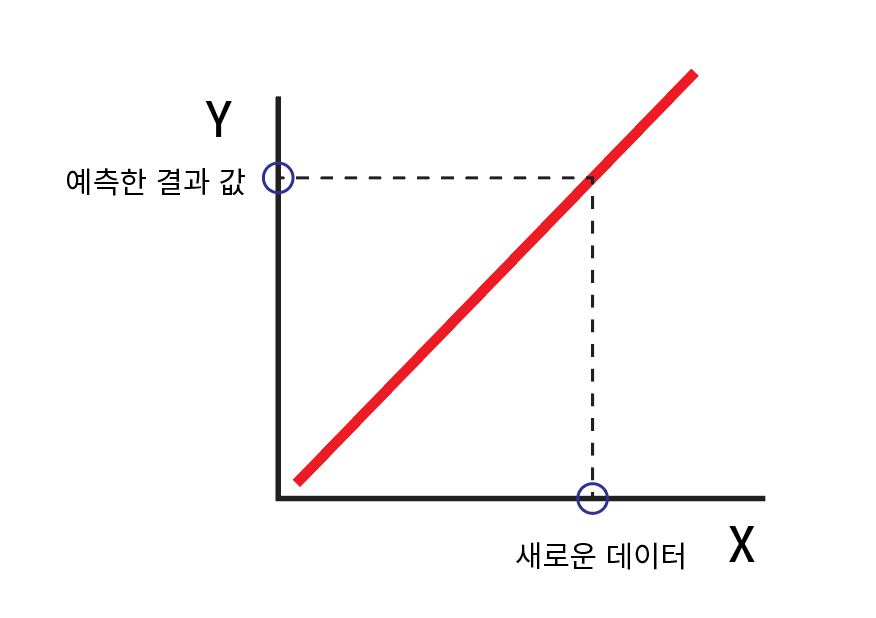
이런식으로 직선을 통해 새로운 데이터가 들어와도 결과 값을 예측할 수 있게 된다.
그렇다면 우리는 이러한 직선(회귀선)을 어떻게 구할 수 있을까?
이때 확률적으로 x만으로 y를 100% 표현할 수 있다면 y=Wx 라는 식으로 표현할 수 있을 것이다.
예를 들어 다음 데이터로 회귀선을 예측해보자.
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
이때 회귀선은 어떻게 될까?
y = 2x 라는 식으로 표현할 수 있을 것이다.
그런데 데이터가 이런식이라면 어떨까?
| x | y |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
y = 2x +1 이렇게 표현할 수 있지 않을까?
위 데이터처럼 x변수만으로 y를 100% 표현할 수 없을 때 우리는 회귀식에 상수항을 더해줘야 한다.
정리하자면 회귀선은 다음과 같이 표현할 수 있다.
그러면 어떠한 회귀선이 가장 좋은 회귀선일까?
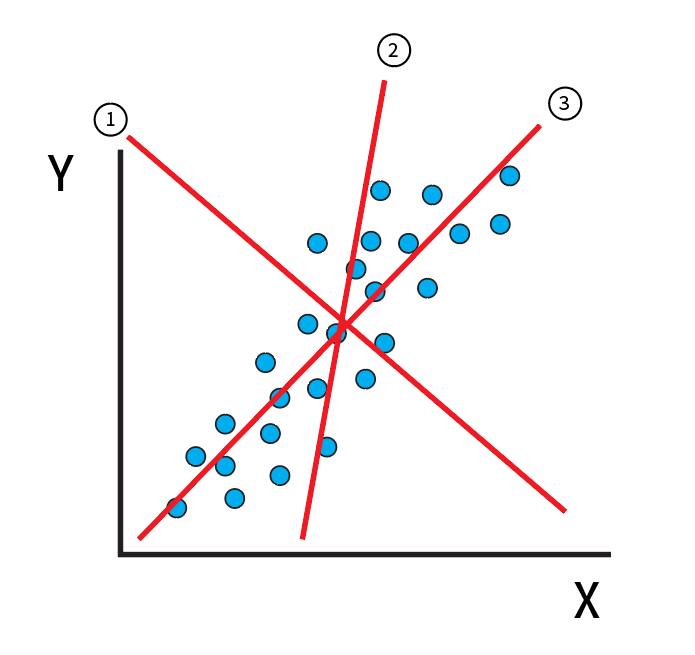
위 그림을 보면 우리는 3번 회귀선이 가장 좋은 회귀선이라는 것을 본능적으로 알 수 있다. 데이터들을 가장 잘 나타낼 수 있는 회귀선의 기준은 y값과 비교해서 오차를 합하여 알 수 있다.
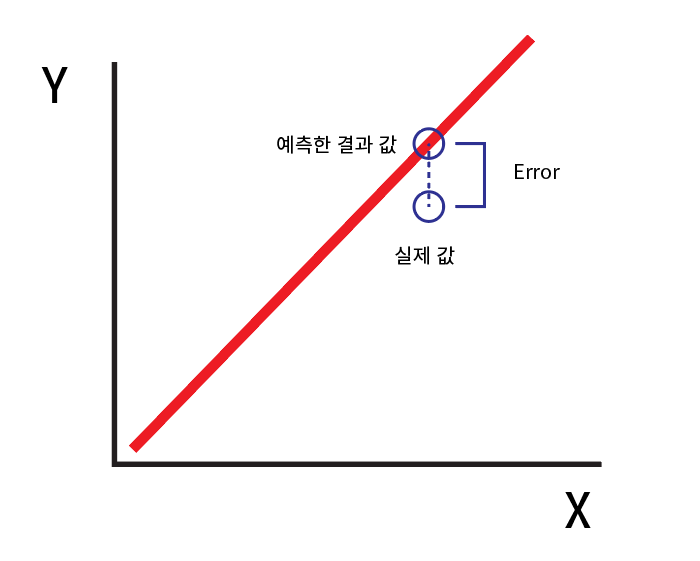
위 그림처럼 실제 값 - 예측한 값 을 통해 오차(error)를 구할 수 있다. 이러한 오차가 작을수록 좋은 회귀선일 것이다.
여기서 오차를 cost(비용)라고도 하는데 각 예측값과 실제 값을 전부 합하는 cost function을 총 cost를 구하고 cost를 줄여가면 가장 좋은 회귀선을 구할 수 있을 것이다.
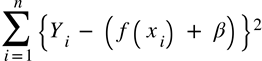
실제 값 y와 예측값 {f(x) + b} 의 차이를 전부 합치면 되는데 이때 왜 제곱을 하여 더해줄까?
오차가 2, -2, 3, -3이라고 하면 오차의 합을 단순히 더한다면 0이 될것이다. 이렇게 음수로 인한 총합의 감소를 막고자 절대값을 취하거나 제곱을 통해 코스트를 구하게 된다.
이 코스트함수를 미분하여 미분 값이 0이면 cost의 최저점을 구할 수 있을 것이다.
다음 글에서는 이 코스트함수를 미분하는 Gradient Descent의 개념과 간단한 예제를 코드를 통하여 구현해보자.