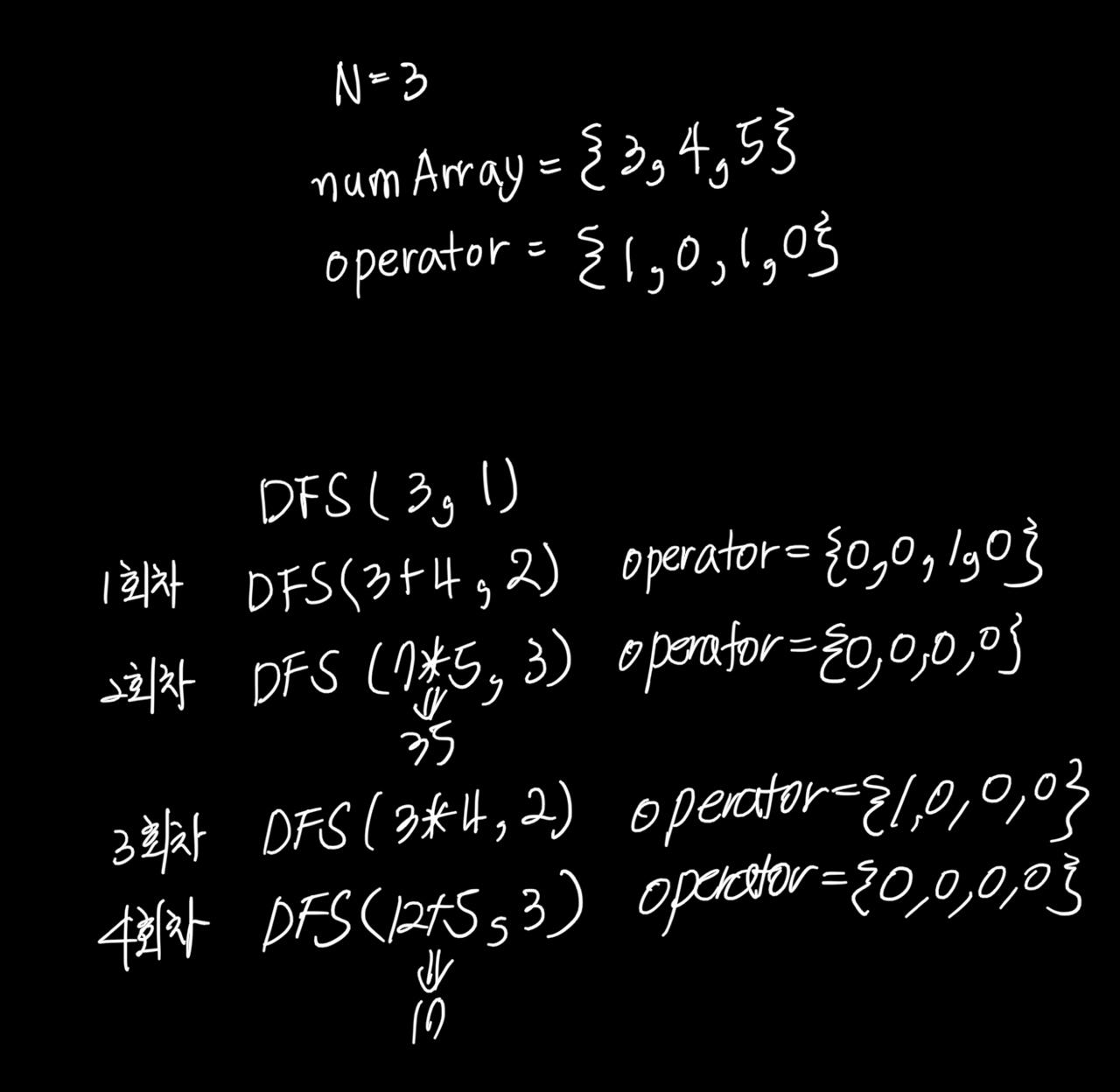[JAVA/14888번] 연산자 끼워넣기

---

문제

---

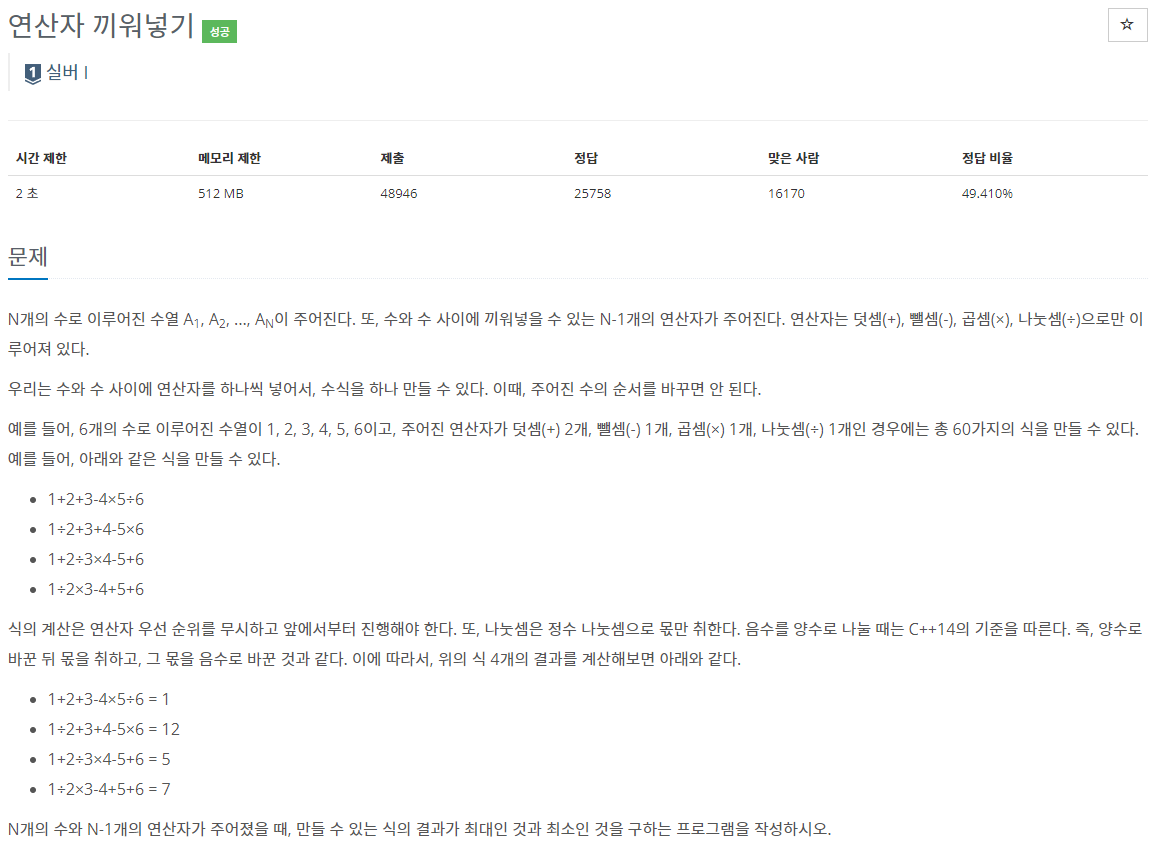
입력 및 출력

---

풀이

import java.io.*;

class Main {
    public static int MAX = Integer.MIN_VALUE;
    public static int MIN = Integer.MAX_VALUE;
    public static int[] numArray;
    public static int[] operator = new int[4];
    public static int N;

    public static void main(String args[]) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        // 수의 개수 N(2 <= N <= 11)
        N = Integer.parseInt(br.readLine());

        // N개의 숫자를 입력받는다.
        String[] temp = br.readLine().split(" ");

        // N의 크기를 갖는 정수형 배열을 선언한다.
        numArray = new int[N];
        for (int i = 0; i < N; i++) {
            numArray[i] = Integer.parseInt(temp[i]);
        }

        // 연산자의 개수를담을 배열 (+, -, *, / 순으로 구성된다.)
        String[] temp2 = br.readLine().split(" ");

        // 연산자의 개수를 담을 배열
        for (int i = 0; i < operator.length; i++) {
            operator[i] = Integer.parseInt(temp2[i]);
        }

        DFS(numArray[0], 1);

        // 결과 값 출력
        System.out.println(MAX);
        System.out.println(MIN);
    }

    public static void DFS(int number, int index) {
        if (index == N) {
            MAX = Math.max(MAX, number);
            MIN = Math.min(MIN, number);
        }

        for (int i = 0; i < 4; i++) {
            if (operator[i] > 0) {
                // operator의 개수를 1 감소
                operator[i]--;

                // i에 매핑되는 결과 값에 조건을 실행
                switch (i) {
                    case 0:
                        DFS(number + numArray[index], index + 1);
                        break;
                    case 1:
                        DFS(number - numArray[index], index + 1);
                        break;
                    case 2:
                        DFS(number * numArray[index], index + 1);
                        break;
                    case 3:
                        DFS(number / numArray[index], index + 1);
                        break;
                }
                // 다시 operator의 개수를 증가
                operator[i]++;
            }
        }
    }
}

---

결과 및 해결방법

[결과]

[정리]

해결방법
이번 문제는 N개의 수열로 이루어진 숫자 사이에 N-1개의 연산자를 넣어 최댓값과 최솟값을 구하는 문제이다.

브루트포스와 관련된 문제이기 때문에, 숫자와 연산자를 조합하여 만들 수 있는 모든 경우의 수를 탐색하는 것이 이 문제를 해결하는 키 포인트이다.

모든 경우의 수를 탐색하기 위한 DFS함수를 생성하고, 인자로 N개의 숫자 중 첫 번째 숫자와 깊이를 알기 위한 인덱스 값을 넘겨주었다.
=> DFS(numArray[0], 1)

자, 이제 본격적으로 DFS함수를 분석해보자!

가장 먼저, DFS함수의 첫 번째 조건을 보면 인덱스의 값이 N과 동일하다면 Math함수를 사용하여 최댓값과 최솟값을 대입하였다.

두 번째로, 연산자의 개수만큼 반복문을 수행한다. 연산자의 개수는 operator배열에 존재하고 +, -, *, /로 구성되기 때문에 4번 반복 수행한다.

operator배열의 i번째 인덱스가 0보다 클 경우, operator배열의 i번째 요소를 1 감소시키고 스위치-케이스문을 통해 맞는 조건을 찾아 재귀함수를 호출하였다.

그 후가 중요한데, 스위치-케이스문 뒤를 보면 operator배열의 i번째 요소를 1증가 시켜주는 것을 확인할 수 있다. 이로써 다시 모든 원소의 개수가 돌아오게 되고 반복문을 반복해서 수행할 수 있게 된다.

이와 같은 문제풀이 방식은 최적의 해를 찾을 수 있지만, 시간이 많이 걸린다는 단점이 있다.

[이해를 위한 예시]