문제
입력 및 출력
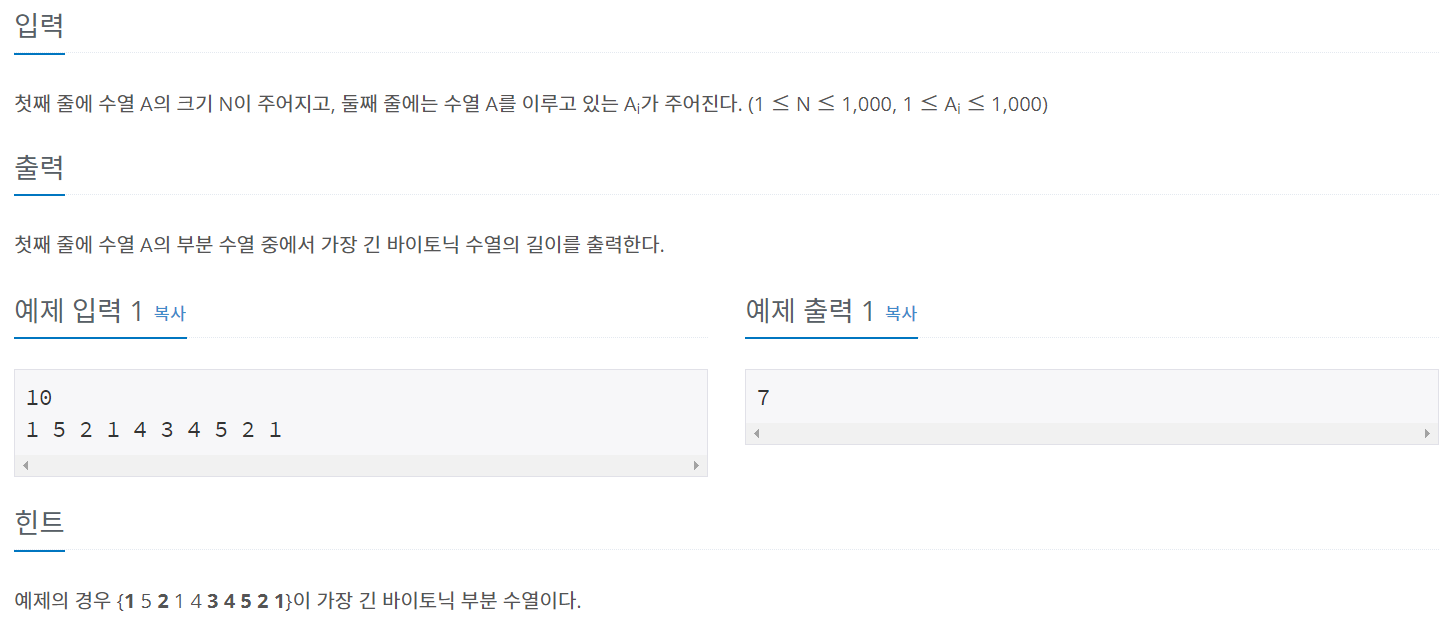
풀이
import java.io.*;
class Main {
public static void main(String args[]) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 수열의 크기N
int N = Integer.parseInt(br.readLine());
// N의 크기를 갖는 수열 A
String[] temp = br.readLine().split(" ");
// temp배열을 숫자배열로 변환
int[] A = new int[N];
for (int i = 0; i < N; i++) {
A[i] = Integer.parseInt(temp[i]);
}
// RDP
int[] RDP = new int[N];
// 수열의 크기인 N만큼 반복문을 수행한다.
for (int i = 0; i < N; i++) {
// 해당 위치에 원소 자신의 개수인 1을 저장한다.
RDP[i] = 1;
// 0부터 i번째 - 1까지 반복문을 수행한다.
for (int j = 0; j < i; j++) {
// A배열의 i번째 원소가 j번째 원소보다 크고, RDP배열의 i번째 원소가 j번째 원소 + 1보다 값이 작을경우, 값을 변경한다.
if (A[j] < A[i] && RDP[i] < RDP[j] + 1) {
RDP[i] = RDP[j] + 1;
}
}
}
// LDP
int[] LDP = new int[N];
for (int i = N - 1; i >= 0; i--) {
LDP[i] = 1;
for (int j = N - 1; j > i; j--) {
if (A[j] < A[i] && LDP[i] < LDP[j] + 1) {
LDP[i] = LDP[j] + 1;
}
}
}
// MAX
int max = -1;
// RDP와 LDP의 부분수열 길이의 합 중 최댓값
for (int i = 0; i < N; i++) {
if (max < LDP[i] + RDP[i]) {
max = LDP[i] + RDP[i];
}
}
// 중복제거를 위해 -1을 더한 후 결과 값 출력
System.out.println(max - 1);
}
}결과 및 해결방법
[결과]
[정리]
해결방법
눈으로 수열을 보고 가장 긴 부분수열을 찾는 과정은 쉬었으나, 이를 코드로 구현하는 것은 생각보다 까다로웠다.
문제에서 나타난 예제를 통해 나올 수 있는 경우의 수는 총 세가지로 오름차순으로 이루어진 순열, 내림차순으로 이루어진 순열, 특정 값을 기준으로 왼쪽부분은 오름차순이고 오른쪽부분은 내림차순인 순열이 있다.
문제에서 예로 나타낸 {1, 5, 2, 1, 4, 3, 4, 5, 2, 1}을 통해 문제를 이해해보자.
가장 먼저 왼쪽에서 오른쪽으로 진행하는 오름차순의 경우, 원소별 수열의 길이를 보면 다음과 같이 나타낼 수 있다.
RDP의 원소의 각 인덱스의 길이를 나타내보자!
RDP[0] = {1} => 길이 1
RDP[1] = {1, 5} => 길이 2
RDP[2] = {1, 2} => 길이 2
RDP[3] = {1} => 길이 1
RDP[4] = {1, 2, 4} => 길이 3
RDP[5] = {1, 2, 3} => 길이 3
RDP[6] = {1, 2, 3, 4} => 길이 4
RDP[7] = {1, 2, 3, 4, 5} => 길이 5
RDP[8] = {1, 2} => 길이 2
RDP[9] = {1} => 길이 1
다음으로 오른쪽에서 왼쪽으로 진행하는 오름차순 부분수열을 구해보자!
RDP[9] = {1} => 길이 1
RDP[8] = {1, 2} => 길이 2
RDP[7] = {1, 2, 5} => 길이 3
RDP[6] = {1, 2, 4} => 길이 3
RDP[5] = {1, 2, 3} => 길이 3
RDP[4] = {1, 2, 3, 4} => 길이 4
RDP[3] = {1} => 길이 1
RDP[2] = {1, 2} => 길이 2
RDP[1] = {1, 2, 3, 4, 5} => 길이 5
RDP[0] = {1} => 길이 1
왼쪽에서 오른쪽으로, 오른쪽에서 왼쪽으로의 수열을 구할 수 있었다. 가장 긴 부분수열을 구하기 위해 두 수열을 합쳐보겠다.
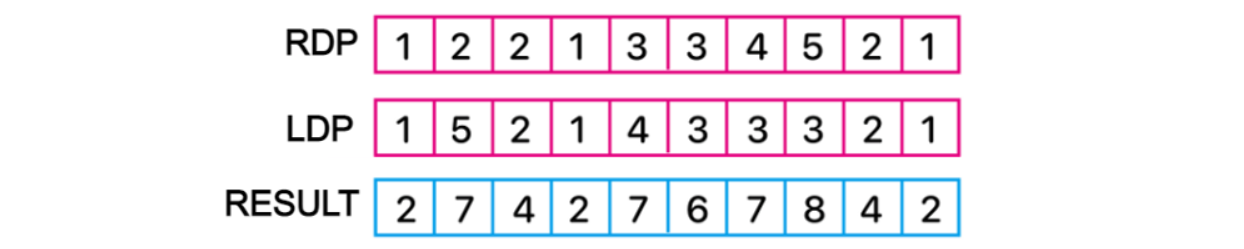위 그림에서 보았듯이 오름차순 수열과 내림차순 수열을 합쳐서 가장 긴 수열을 구할 수 있다. 이때, 두 배열을 단순히 합한 결과이기 때문에 중복되는 수를 제거하기 위해 -1을 수행해주어야 한다.
다음 결과 배열을 아래와 같이 나타낼 수 있다.
RESULT[0] = (RDP[0] + LDP[0]) = {1} + {1} = {1} => 길이 1
RESULT[1] = (RDP[1] + LDP[1]) = {1, 5} + {5, 4, 3, 2, 1} = {1, 5, 4, 3, 2, 1} => 길이 6
RESULT[2] = (RDP[2] + LDP[2]) = {1, 2} + {2, 1} = {1, 2, 1} => 길이 3
RESULT[3] = (RDP[3] + LDP[3]) = {1} + {1} = {1} => 길이 1
RESULT[4] = (RDP[4] + LDP[4]) = {1, 2, 4} + {4, 3, 2, 1} = {1, 2, 4, 3, 2, 1} => 길이 6
RESULT[5] = (RDP[5] + LDP[5]) = {1, 2, 3} + {3, 2, 1} = {1, 2, 3, 2, 1} => 길이 5
RESULT[6] = (RDP[6] + LDP[6]) = {1, 2, 3, 4} + {4, 2, 1} = {1, 2, 3, 4, 2, 1} => 길이 6
RESULT[7] = (RDP[7] + LDP[7]) = {1, 2, 3, 4, 5} + {5, 2, 1} = {1, 2, 3, 4, 5, 2, 1} => 길이 7
RESULT[8] = (RDP[8] + LDP[8]) = {1, 2} + {2, 1} = {1, 2, 1} => 길이 3
RESULT[9] = (RDP[9] + LDP[9]) = {1} + {1} = {1} => 길이 1
따라서 길이가 가장 긴 7이 정답이 될 것이다. 이제 코드 부분으로 이동하자!
[이해를 위한 예시]
