[JAVA/17087번] 숨바꼭질 6

문제

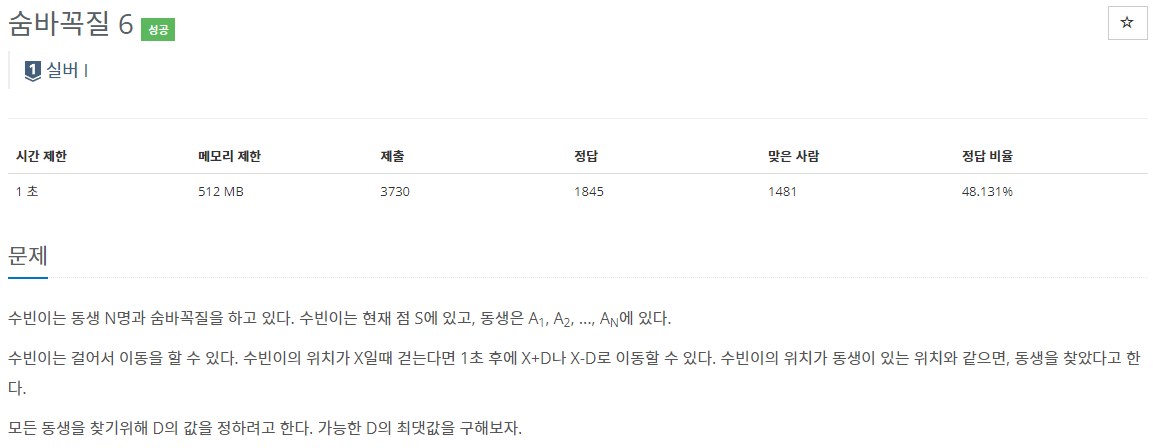
입력 및 출력

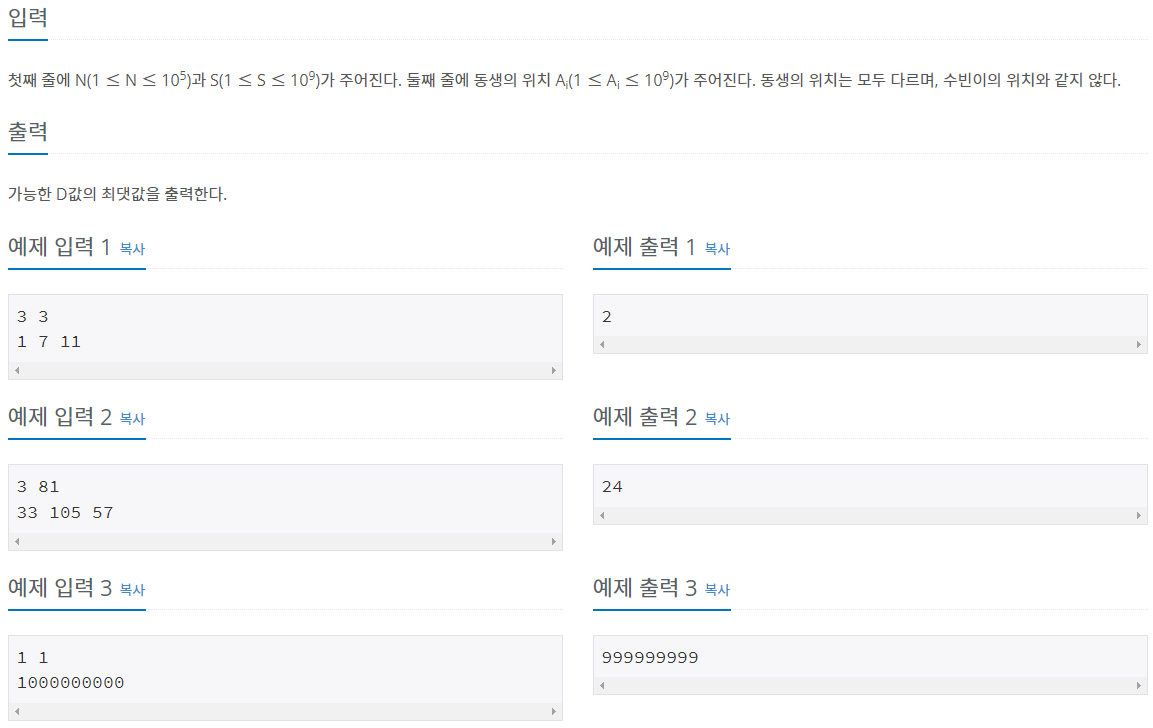
풀이

import java.io.*;

class Main {
    public static int gcd(int A, int B) {
        if (B == 0) {
            return A;
        } else {
            return gcd(B, A % B);
        }
    }

    public static void main(String args[]) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] strArray = br.readLine().split(" ");

        // N, S
        int N = Integer.parseInt(strArray[0]);
        int S = Integer.parseInt(strArray[1]);

        // 동생들의 위치
        String[] position = br.readLine().split(" ");

        // 나와 동생들의 거리
        int[] distance = new int[N];
        for (int i = 0; i < position.length; i++) {
            // 나의 거리에서 동생의 거리를 뺀 값을 num에 저장
            int num = S - Integer.parseInt(position[i]);

            // 음수를 양수로 전환
            if (num < 0) {
                num = num * -1;
            }

            distance[i] = num;
        }

        // 나와 동생들 거리의 최대공약수
        int result = distance[0];
        for (int i = 1; i < N; i++) {
            result = gcd(result, distance[i]);
        }

        // 결과값 출력
        System.out.println(result);
    }
}

결과 및 해결방법

[결과]

[정리]

해결방법

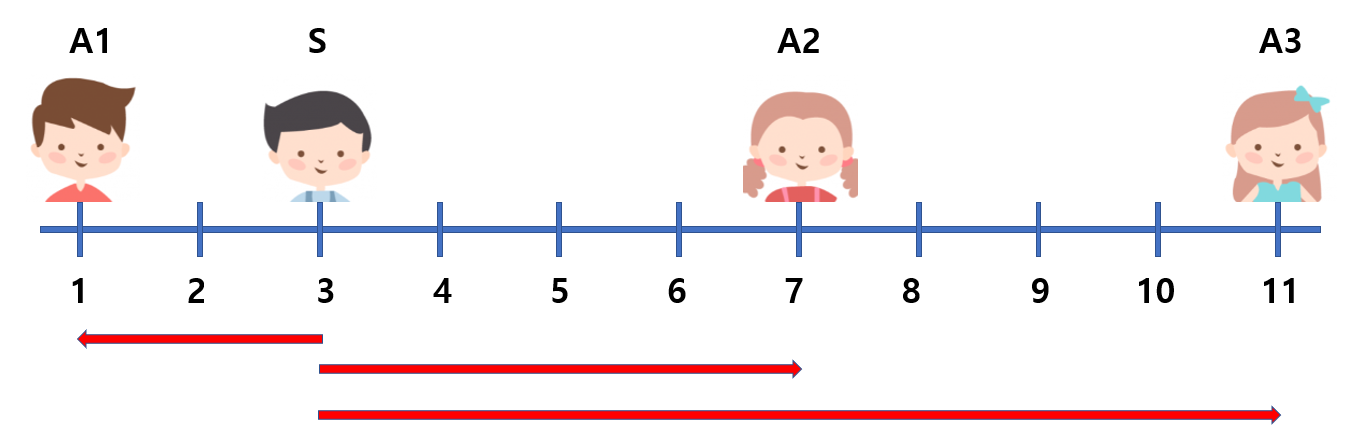
수빈이의 위치 S와 동생들의 수 N을 입력받는다. 동생들의 수 만큼 동생들의 위치를 입력받아 배열에 넣어준다.

위 그림을 참고하면 수빈이(S)를 기준으로 각 동생들의 거리를 뺸다. 만약 뺀 거리가 음수일 경우 -1을 곱하여 양수로 만들어준다. 그 후, 나와 동생들의 거리를 저장할 distance배열에 넣어준다.

모든 동생들을 찾기위한 D의 값을 구하고 있으므로 distance배열의 각 원소별 최대공약수를 구하면 D값을 찾을 수 있다.