[JAVA/2225번] 합분해

문제

입력 및 출력

풀이

import java.io.*;

class Main {
    public static void main(String args[]) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] strArray = br.readLine().split(" ");
        
        // N, K
        int N = Integer.parseInt(strArray[0]);
        int K = Integer.parseInt(strArray[1]);

        // N을 K개의 수를 통해 만들때 결과 값을 넣을 배열 DP
        int[][] DP = new int[N + 1][K + 1];

        // 1부터 K개까지 반복문을 수행
        for (int i = 1; i <= K; i++) {
            // i개수를 갖고 1을 만들 수 있는 경우의 수는 i개이다.
            // DP[1][2] = (0,1),(1,0)
            // DP[1][3] = (0,0,1),(0,1,0),(1,0,0)
            DP[1][i] = i;
        }

        // 1부터 N개까지 반복문을 수행
        for (int i = 1; i <= N; i++) {
            // 1개로 i를 만들 수 있는 경우의 수는 1개이다.
            // DP[2][1] = (2)
            // DP[3][1] = (3)
            DP[i][1] = 1;
        }

        // 1에대한 처리는 수행했기 때문에 2부터 N과 K개 까지의 반복문 수행
        for (int i = 2; i <= N; i++) {
            for (int j = 2; j <= K; j++) {
                DP[i][j] = (DP[i][j - 1] + DP[i - 1][j]) % 1000000000;
            }
        }

        // 결과 값 출력
        System.out.println(DP[N][K]);
    }
}

결과 및 해결방법

[결과]

[정리]

해결방법
N이 0일 경우
K=1 => (0)
K=2 => (0+0)
K=3 => (0+0+0)

N이 1일 경우
K=1 => (1)
K=2 => (0+1), (1+0)
k=3 => (1+0+0), (0+1+0), (0+0+1)

N이 2일 경우
K=1 => (2)
K=2 => (1+1), (2+0), (0+2)
K=3 => (0+0+2), (0+2+0), (2+0+0), (1+1+0), (1+0+1), (0+1+1)

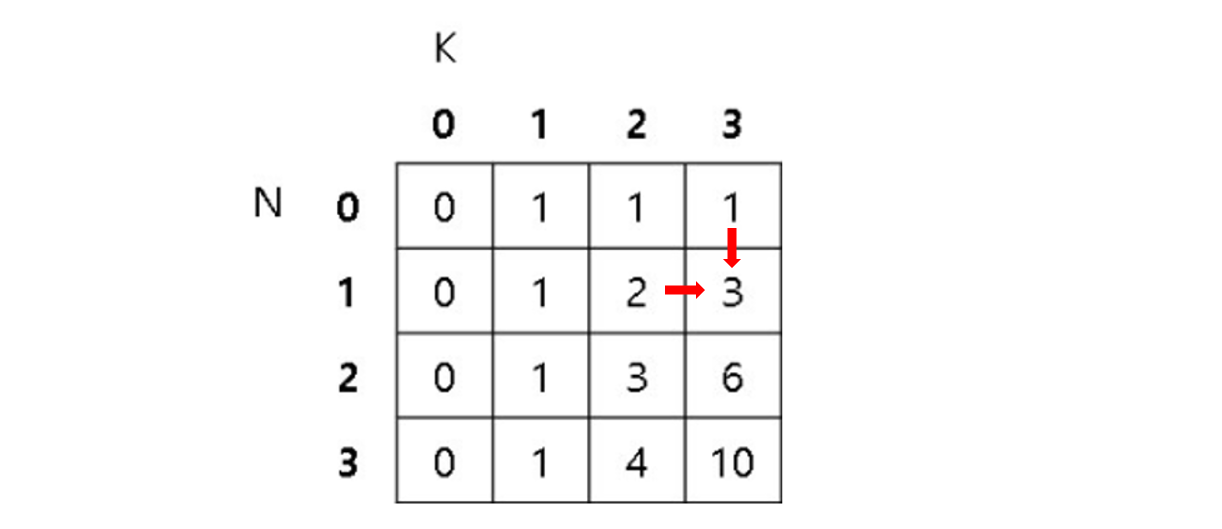
위 정보를 토대로 점화식을 작성해보자!
DP[1][3] = DP[0][3] + DP[1][2]
=> DP[N][K] = DP[N-1][K] + DP[N][K-1]의 공식을 확인할 수 있고, 식을 적용시켜보자!