목차

자료구조

• Stack
• Queue
• Tree
• Binary Search Tree
• Graph

알고리즘

• DFS
• BFS

자료구조

자료구조란?
여러 데이터의 묶음을 저장하고 사용하는 방법을 정의한 것
=> 1)데이터 저장 2) 사용하는 방법 정의

자료구조는 자료(데이터)를 다루는 구조 그 자체를 뜻하며, 구현하는 방식에는 제약이 없습니다

데이터란?
문자, 소리, 그림, 영상 등 실생활을 구성하고 있는 모든 값

데이터 그 자체만으로는 어떤 정보를 가지기 힘들다
그러므로 분석하고 정리하여 활용해야만 의미를 가질 수 있다
사용하려는 목적에 따라 형태를 구분하고 분류하여 사용할 수 있다

데이터를 정해진 규칙 없이 저장하거나 하나의 구조로만 정리하고 활용하는 것보다 데이터를 체계적으로 정리하여 저장해두는 게 데이터를 활용하는 데 있어 훨씬 유리

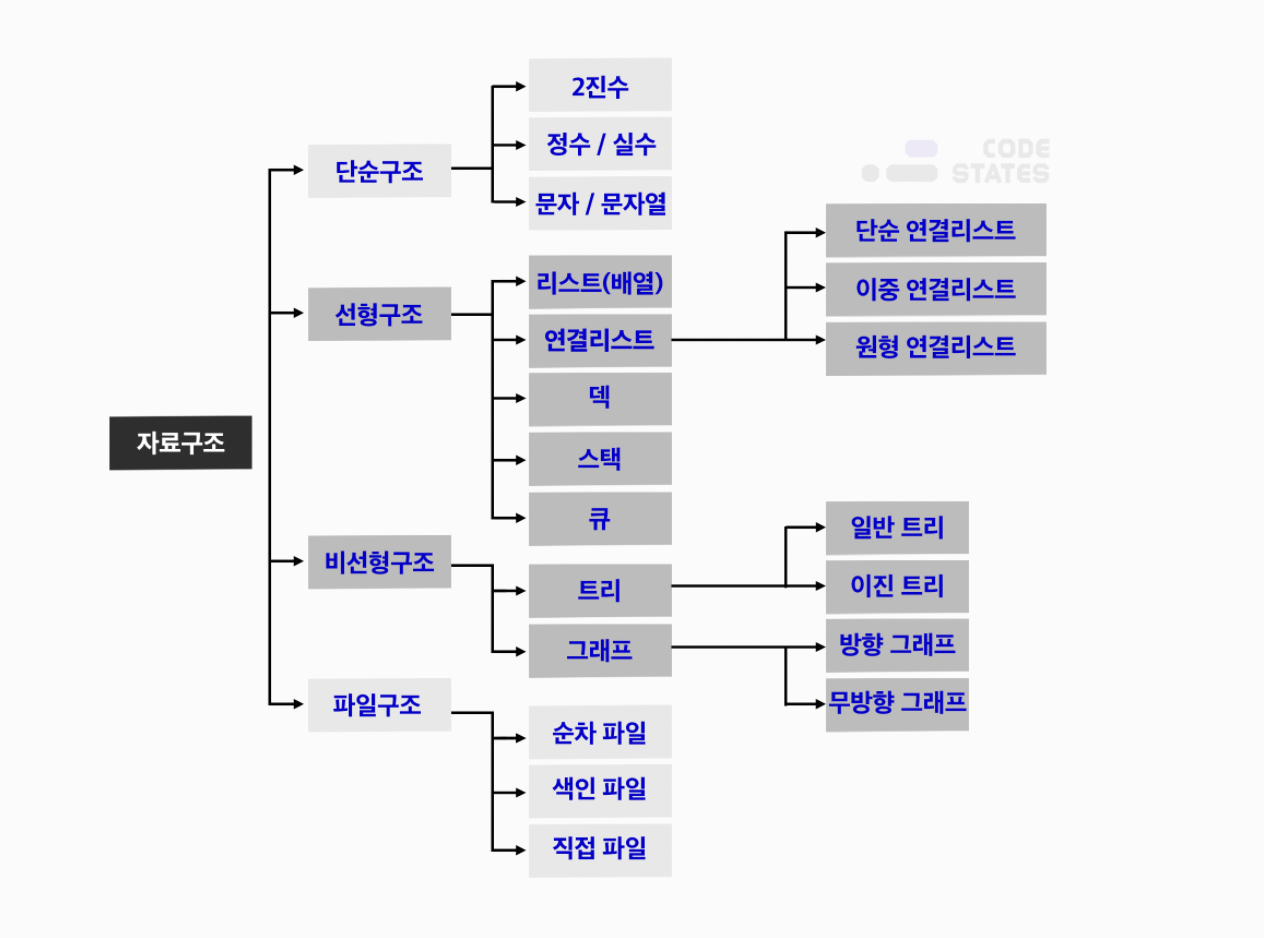
선형구조 : 순서대로
비선형구조 : 순서 없음

대부분의 자료구조는 특정한 상황에 놓인 문제를 해결하는 데에 특화되어 있다
그러므로 많은 자료구조를 알아두면 어떠한 상황이 닥쳤을 때 적합한 자료구조를 빠르고 정확하게 적용하여 문제를 해결할 수 있다.
=> 자료구조를 알면 알고리즘을 풀기 좋다

1. 각 자료구조가 가진 특징을 학습
2. 각 자료구조를 사용하기 적합한 상황을 이해한다
3. 자료구조 내부를 직접 구현한다 : 다른 자료구조와의 차이점 이해, 동작원리 이해
   => class를 이용해서 정의, 속성과 메서드를 학습
   => 자료구조를 활용해 알고리즘을 푼다 - 문제를 풀기에 적합한 자료구조를 파악하고 사용한다
   알고리즘 문제를 만날 때마다 필요한 자료구조를 클래스로 직접 정의해서 풀기에는 다소 많은 시간이 소요됩니다. 그러므로 JavaScript에서 제공하는 배열(Array)과 같은 데이터 타입을 이용해 자료구조의 형태와 유사하게 구현하여 문제를 해결합니다.

Stack

데이터를 순서대로 쌓는 자료구조
입력과 출력이 하나의 방향으로 이루어지는 제한적 접근

• LIFO : 마지막으로 들어온 것이 가장 먼저 나간다
• FILO : 가장 먼저 들어간 것이 가장 나간 것

Stack의 실사용 예제
-브라우저의 뒤로 가기, 앞으로 가기 기능 구현 시
1. 새로운 페이지로 접속할 때 : 현재 페이지를 Prev Stack에 보관합니다.
2. 뒤로 가기 : 현재 페이지를 Next Stack에 보관하고
Prev Stack에 가장 나중에 보관된 페이지를 현재 페이지로 가져옵니다.
3. 앞으로 가기 : Next Stack의 가장 마지막으로 보관된 페이지를 가져옵니다.
마지막으로 현재 페이지를 Prev Stack에 보관합니다.

Queue

FIFO : 먼저 들어간 데이터가 먼저 나온다
LILO : 마지막에 넣은 데이터가 마지막에 나온다

데이터(data)가 입력된 순서대로 처리할 때 주로 사용합니다.

Queue의 실사용 예제
-컴퓨터와 연결된 프린터에서 여러 문서를 순서대로 인쇄할 때 사용
1. 문서를 작성하고 출력 버튼을 누르면 해당 문서는 인쇄 작업 (임시 기억 장치의)Queue에 들어간다
2. 프린터는 인쇄 작업 queue에 들어온 문서를 순서대로 인쇄한다

컴퓨터 장치들 사이에서 데이터를 주고받을 때, 각 장치 사이에 존재하는 속도의 차이나 시간 차이를 극복하기 위해 임시 기억 장치의 자료구조로 queue를 사용한다
이것을 통틀어 버퍼라고 한다

대부분의 컴퓨터 장치에서 발생하는 이벤트는 파동 그래프와 같이 불규칙적으로 발생한다
CPU와 같이 발생한 이벤트를 처리하는 장치는 일정한 처리 속도를 갖는다
불규칙적으로 발생한 이벤트를 규칙적으로 처리하기 위해 버퍼를 사용한다

프린터는 속도가 느리다
CPU는 프린터와 비교하여 데이터를 처리하는 속도가 빠르다
따라서 CPU는 빠른 속도로 인쇄에 필요한 데이터를 만든 다음

• 인쇄 작업 queue에 저장하고 다른 작업 수행
• 프린터는 인쇄 작업 queue에서 데이터를 받아 일정한 속도로 인쇄한다

1. 사용자 정의 데이터 타입(class)로 구현해서 사용하기 vs 배열 사용하기

사용자 정의 데이터 타입을 구현해서 Stack과 Queue를 사용해도 좋습니다.
그러나 JavaScript에는 Array라는 훌륭한 자료형이 이미 있습니다.
Array를 사용하면 1)사용자 정의 데이터 타입을 구현하는 시간을 절약할 수 있고,
2) 몇 가지의 메서드로 Stack과 Queue처럼 동작하도록 사용할 수 있습니다.

자료구조는 자료(데이터)를 다루는 구조 그 자체를 뜻하며, 구현하는 방식에는 제약이 없습니다

배열로 자료구조 Stack 구현하기

// const array = new Array() 미리 정의된 Array 객체를 사용합니다.

const stack = []; 

stack.push(1); // [1]
stack.push(2); // [1, 2]
stack.push(3); // [1, 2, 3]
stack.push(4); // [1, 2, 3, 4]
stack.push(5); // [1, 2, 3, 4, 5]

console.log(stack); // [1, 2, 3, 4, 5]

stack.pop(); // [1, 2, 3, 4]
stack.pop(); // [1, 2, 3]

console.log(stack); // [1, 2, 3]

Stack 구현하기

class Stack {
  constructor() {
    this.storage = {};
    this.top = 0; // 스택의 가장 상단을 가리키는 포인터 변수를 초기화 합니다.
  }

  size() {
    return this.top;
  }

	// 스택에 데이터를 추가 할 수 있어야 합니다.
  push(element) {
    this.storage[this.top] = element;
    this.top += 1;
  }
	
	// 가장 나중에 추가된 데이터가 가장 먼저 추출되어야 합니다.
  pop() {
    // 빈 스택에 pop 연산을 적용해도 에러가 발생하지 않아야 합니다
    if (this.top === 0) {
      return;
    }

    const result = this.storage[this.top-1];
    //변수에 넣는 이유 : delete하면 top이 달라지니까
    //1개있을 때 0번째 인덱스니까 
    delete this.storage[this.top-1];
    this.top -= 1;
    
    return result;
  }
}

배열로 자료구조 Queue 구현하기

// const array = new Array() 미리 정의된 Array 객체를 사용합니다.

const queue = []; 

queue.push(1); // [1]
queue.push(2); // [1, 2]
queue.push(3); // [1, 2, 3]
queue.push(4); // [1, 2, 3, 4]
queue.push(5); // [1, 2, 3, 4, 5]

console.log(queue); // [1, 2, 3, 4, 5]

queue.shift(); // [2, 3, 4, 5]
queue.shift(); // [3, 4, 5]

console.log(queue); // [3, 4, 5]

Queue 구현하기

class Queue {
  constructor() {
    this.storage = {};
    this.front = 0;
    this.rear = 0;
  }

  size() {
    return this.rear-this.front;
    //this.rear에 마지막에 +1을 해서 성립
  }
	
	// 큐에 데이터를 추가 할 수 있어야 합니다.
  enqueue(element) {
    this.storage[this.rear] = element; // 1 : 2 ~ 8:9 
    this.rear += 1; //+9
  }
	
	// 가장 먼저 추가된 데이터가 가장 먼저 추출되어야 합니다.
  dequeue() {
    // 빈 큐에 dequeue 연산을 적용해도 에러가 발생하지 않아야 합니다
    if (this.rear === this.front) {
      return;
    }

    const result = this.storage[this.front];
    delete this.storage[this.front];
    this.front += 1;//1

    return result;
  }
}

Graph

자료구조의 그래프는 여러 개의 점들이 선으로 이어져 있는 복잡한 네트워크망과 같은 모습
여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조

직접적인 관계 : 두 점 사이를 이어주는 선이 있다
간접적인 관계 : 몇 개의 점과 선에 걸쳐 이어진다
=> 관계가 있다

간선은 관계가 있음을 의미
간접적으로도 간선으로 이어지지 않으면 관계가 없음

가중치 : 연결의 강도가 얼마나 되는지
가중치 그래프 : 추가적인 정보를 파악할 수 있는 그래프

• 연결의 강도(추가적인 정보)가 얼마나 되는지 적혀져 있는 그래프
  비가중치 그래프 : 추가적인 정보를 파악할 수 없는 그래프

• 연결의 강도가 적혀져 있지 않는 그래프

  무방향 그래프 : 정점 사이 양방향
  단방향 그래프 : 한쪽 방향만 가능

  진입 차수 : 한 정점에 진입(들어오는 간선)의 개수
  진출 차수 : 진출(나가는 간선)의 개수

  인접 : 두 정점 간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점

  자기루프 : 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기루프를 가졌다고 한다
  다른 정점을 거치지 않는다는 것이 특징

  사이클 : 한 정점에서 출발해 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다

  정점(vertex): 하나의 점 (노드), 그래프의 기본 원소

• 인접 정점 : 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점
  간선(edge) : 하나의 선, 정점 간의 관계 나타낸다

  그래프의 실사용 예제

• 포털 사이트의 검색 엔진,

• SNS에서 사람들과의 관계,

• 내비게이션 (길 찾기) 등에서 사용하는 자료구조

세 가지 모두 수많은 정점을 가지고 있고, 서로 관계가 있는 정점은 간선으로 이어져 있습니다. 세 가지 중에서 내비게이션 시스템이 어떤 방식으로 자료구조 그래프를 사용하는지 살펴보겠습니다.

질문
위 내비게이션 예제에서 서울은 몇 개의 진입차수와 몇 개의 진출차수를 가지고 있나요?
내비게이션 대신 SNS에서 자료구조로 그래프를 이용한다면, 정점과 간선은 무엇이 될까요?
SNS에서 어떤 관계일 경우 단방향 그래프가 생성될까요?
자기 루프와 사이클은 어떻게 다를까요?

그래프 표현방식1 : 인접 행렬

두 정점을 이어주는 간선이 있다면 두 정점은 인접하다
인접 행렬 : 서로 다른 정점들이 인접한 상태인지를 표시한 행렬, 2차원 배열의 형태
이어져 있으면 true(1), 아니면 false(0)
만약 가중치 그래프라면 1 대신 관계에서 의미 있는 값을 저장한다

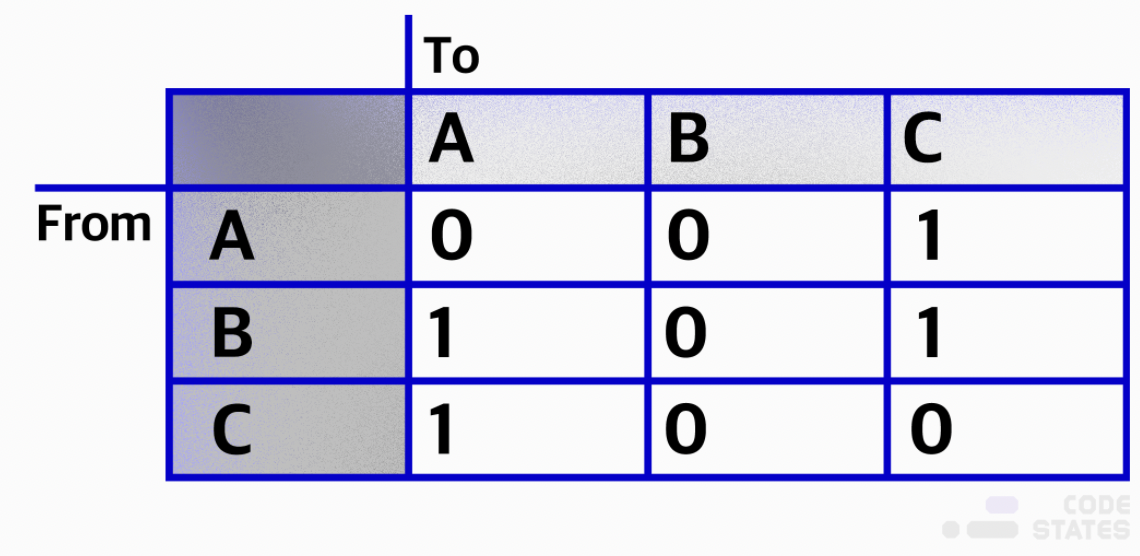
A의 진출차수는 1개 입니다: A —> C
[0][2] === 1
B의 진출차수는 2개 입니다: B —> A, B —> C
[1][0] === 1
[1][2] === 1
C의 진출차수는 1개입니다: C —> A

• [2][0] === 1

인접 행렬은 언제 사용할까?
한 개의 큰 표와 같은 모습을 한 인접 행렬은 두 정점 사이에 관계가 있는지, 없는지 확인하기에 용이합니다.
예를 들어, A에서 B로 진출하는 간선이 있는지 파악하기 위해선 0 번째 줄의 1 번째 열에 어떤 값이 저장되어 있는지 바로 확인할 수 있습니다.
가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용됩니다.

// directed graph (방향 그래프)
// unweighted (비가중치)
// adjacency matrix (인접 행렬)
// 이해를 돕기 위해 기존 배열의 인덱스를 정점으로 사용합니다 (0, 1, 2, ... --> 정점)

class GraphWithAdjacencyMatrix {
	constructor() {
		this.matrix = [];
	}

	addVertex() {
        //버텍스를 추가합니다.
		const currentLength = this.matrix.length; 
		for (let i = 0; i < currentLength; i++) {
			this.matrix[i].push(0); 
      //안에 있는 배열 각각에 0을 푸시
		}
		this.matrix.push(new Array(currentLength + 1).fill(0));
    //새로운 배열을 만들어서 추가
	}



	contains(vertex) {
        //TODO: 버텍스가 있는지 확인합니다.
        if(vertex < this.matrix.length){ 
          return true;
        }
        return false; 
	}

	addEdge(from, to) { 
    // 0-> 1
		const currentLength = this.matrix.length;
		if (from === undefined || to === undefined) {
			console.log("2개의 인자가 있어야 합니다.");
			return;
		}
        //TODO: 간선을 추가할 수 없는 상황에서는 추가하지 말아야 합니다.
		if ( to + 1 > currentLength || from + 1 > currentLength || from < 0 || to < 0) {
			console.log("범위가 매트릭스 밖에 있습니다.");
			return;
		}
        //TODO: 간선을 추가해야 합니다.
        this.matrix[from][to] = 1;
	}

	hasEdge(from, to) {
		//TODO: 두 버텍스 사이에 간선이 있는지 확인합니다.
    if(this.matrix[from][to] === 1){ 
      return true;
    }
    return false;
	}

	removeEdge(from, to) {
		const currentLength = this.matrix.length;
		if (from === undefined || to === undefined) {
			console.log("2개의 인자가 있어야 합니다.");
			return;
		}
        //TODO: 간선을 지울 수 없는 상황에서는 지우지 말아야 합니다.
		if (to + 1 > currentLength || from + 1 > currentLength || from < 0 || to < 0) {
      console.log("범위가 매트릭스 밖에 있습니다.");
      return;
		}
        //TODO: 간선을 지워야 합니다.
    else this.matrix[from][to] = 0;

	}
}

그래프 표현방식2 : 인접 리스트

인접 리스트
각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 표현합니다.
각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있습니다.
위 그래프를 인접 리스트로 표현하면 다음 그림과 같습니다.

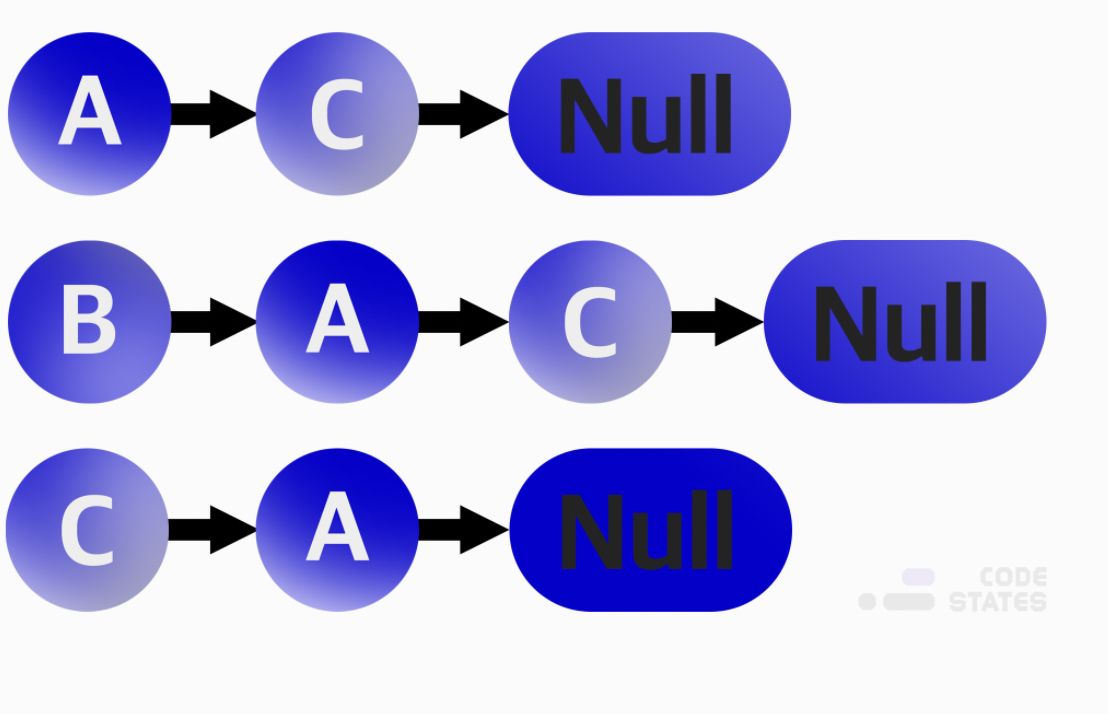
B는 A와 C로 이어지는 간선이 두 개가 있는데, 왜 A가 C보다 먼저죠? 이 순서는 중요한가요?

보통은 중요하지 않습니다. 그래프, 트리, 스택, 큐 등 모든 자료구조는 구현하는 사람의 편의와 목적에 따라 기능을 추가/삭제할 수 있습니다. 그래프를 인접 리스트로 구현할 때, 정점별로 살펴봐야 할 우선순위를 고려해 구현할 수 있습니다. 이때, 리스트에 담긴 정점들을 우선순위별로 정렬할 수 있습니다. 우선순위가 없다면, 연결된 정점들을 단순하게 나열한 리스트가 됩니다.

우선순위를 다뤄야 한다면 더 적합한 자료구조(ex. queue, heap)를 사용하는 것이 합리적입니다. 따라서 보통은 중요하지 않습니다. (언제나 예외는 있습니다.)

인접 리스트는 언제 사용할까?
메모리를 효율적으로 사용하고 싶을 때 인접 리스트를 사용합니다.
인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지합니다.

Tree

Tree는 이름 그대로 나무의 형태를 가지고 있습니다. 정확히는 나무를 거꾸로 뒤집어 놓은 듯한 모습을 가지고 있습니다. 그래프의 여러 구조 중 단방향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아 있다고 해서 트리 구조라고 부릅니다.

마치 가계도와 흡사해 보이는 이 트리 구조는 데이터가 바로 아래에 있는 하나 이상의 데이터에 단방향으로 연결된 계층적 자료구조입니다. 데이터를 순차적으로 나열시킨 선형 구조가 아니라, 하나의 데이터 아래에 여러 개의 데이터가 존재할 수 있는 비선형 구조입니다. 트리 구조는 계층적으로 표현이 되고, 아래로만 뻗어나가기 때문에 사이클이 없습니다.

노드(Node) : 트리 구조를 이루는 모든 개별 데이터
루트(Root) : 트리 구조의 시작점이 되는 노드
부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
자식 노드(Child node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
리프(Leaf) : 트리 구조의 끝 지점이고, 자식 노드가 없는 노드

깊이 (depth) : 루트로부터
트리 구조에서는 루트로부터 하위 계층의 특정 노드까지의 깊이(depth)를 표현할 수 있습니다.
루트 노드는 지면에 있는 것처럼 깊이가 0입니다.
위 그림에서 루트 A의 depth는 0이고, B와 C의 깊이는 1입니다. D, E, F, G의 깊이는 2입니다.

레벨(Level)
트리 구조에서 같은 깊이를 가지고 있는 노드를 묶어서 레벨(level)로 표현할 수 있습니다.
depth가 0인 루트 A의 level은 1입니다. depth가 1인 B와 C의 level은 2입니다. D, E, F, G의 레벨은 3입니다.
같은 레벨에 나란히 있는 노드를 형제 노드(Sibling Node) 라고 합니다.

높이(Height) : 리프로부터
트리 구조에서 리프 노드를 기준으로 루트까지의 높이(height)를 표현할 수 있습니다.
리프 노드와 직간접적으로 연결된 노드의 높이를 표현하며, 부모 노드는 자식 노드의 가장 높은 height 값에 +1한 값을 높이로 가집니다. 트리 구조의 높이를 표현할 때에는 각 리프 노드의 높이를 0으로 놓습니다. 위 그림에서 H, I, E, F, J의 높이는 0입니다. D와 G의 높이는 1입니다. B와 C의 높이는 2입니다. 이때 B는 D의 height + 1 을, C는 G의 height + 1 을 높이로 가집니다. 따라서, 루트 A의 높이는 3입니다.

서브 트리(Sub tree)
트리 구조의 root에서 뻗어 나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리를 서브 트리 라고 부릅니다. (D, H, I)로 이루어진 작은 트리도 서브 트리이고, (B, D, E)나 (C, F, G, J)도 서브 트리입니다.

트리의 실사용 예제

• 컴퓨터의 디렉토리 구조
• 월드컵 토너먼트 대진표
• 가계도(족보)
• 조직도

Binary Search Tree

트리 구조는 편리한 구조를 전시하는 것 외에 효율적인 탐색을 위해 사용

이진 트리

자식 노드가 최대 두개 인 노드들로 구성된 트리
왼쪽 자식 노드와 오른쪽 자식 노드

자료의 삽입, 삭제 방법에 따라 정이진트리, 완전이진트리, 포화이진트리로 나뉜다
정이진 트리 (full binary tree) - 각 노드가 0개 혹은 2개인 자식 노드를 갖는다
포화 이진 트리 (perfect binary tree) - 정이진 트리이면서 완전 이진 트리, 모든 리프 노드의 레벨 동일, 모든 레벨이 가득
완전 이진 트리 (complete binary tree) - 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야 한다

class Tree {
  constructor(value) {
		// constructor로 만든 객체는 트리의 Node가 됩니다.
    this.value = value;
    this.children = [];
  }

	// 트리의 삽입 메서드를 만듭니다.
  insertNode(value) {
		// 값이 어떤 이름으로 만들어지고 어느 위치에 붙는지 떠올리는 것이 중요합니다.
		// TODO: 트리에 붙게 될 childNode를 만들고, children에 넣어야 합니다.
    const childNode = new Tree(value);
    this.children.push(childNode);
  }

	// 트리 안에 해당 값이 포함되어 있는지 확인하는 메서드를 만듭니다.
  contains(value) {
		// TODO: 값이 포함되어 있다면 true를 반환하세요. 
    if (this.value === value) {
      return true;
    }
		// TODO: 값을 찾을 때까지 children 배열을 순회하며 childNode를 탐색하세요.
    for(let child of this.children){ 
      if(child.contains(value)){ 
        //위에서 본인을 찾는 것만으로 클리어
        return true;
      }
    }
		// 전부 탐색했음에도 불구하고 찾지 못했다면 false를 반환합니다.
    return false;
  }
}

이진 탐색 트리

모든 왼쪽 자식의 값이 루트나 부모보다 작고,
모든 오른쪽 자식의 값이 루트나 부모보다 크다

이전 탐색 트리는 균형잡힌 트리가 아니면 입력되는 값의 순서에 따라 한쪽으로 몰리게 될 수 있다
이 경우에는 탐색하는 데 시간이 더 걸리는 경우도 있기 때문에 삽입과 삭제마다 트리의 구조를 재조정하는 과정을 거치는 알고리즘을 추가할 수 있다

트리 순회

특정 목적을 위해 트리의 모든 노드를 한번씩 방문하는 것
3가지 방법 : 트리구조에서 노드를 순차적으로 조회할 대의 순서 (왼 -> 오)

• 전위 순회
  루트에서 시작해 왼쪽의 노드들을 순차적으로 둘러본 뒤 왼쪽이 끝나면 오른쪽 노드를 탐색한다
• 중위 순회
  루트를 가운데에 두고 순회한다. 제일 왼쪽 끝에 있는 노드부터 순회하기 시작
  루트를 기준으로 왼쪽에 있는 노드의 순회가 끝나면 루트를 거쳐 오른쪽에 있는 노드로 이동하여 마저 탐색
• 후위 순회
  루트를 가장 마지막에 순회한다. 왼쪽 끝에 있는 노드부터 순회 시작, 루트를 거치지 않고 오른쪽으로 이동해 순회한 뒤 제일 마지막에 루트 방문

BFS

그래프의 탐색은 하나의 정점에서 시작하여 그래프의 모든 정점들을 한번씩 방문(탐색)
모든 자료를 하나씩 확인해본다는 점은 같다
너비 우선적으로 탐색하는 방법
두 정점 사이의 최단 경로를 찾을 때 사용한다

DFS : 더 오랜 시간, 더 완전

깊이 우선적으로 탐색하는 방법
한 정점에서 시작해서 다음 경로로 넘어가기 전에 해당 경로를 완벽하게 탐색할 때 사용한다
BFS보다 탐색 시간은 조금 오래 걸릴지라도 모든 노드를 완전히 탐색할 수 있다

DFS와 BFS의 장단점은 또 무엇이 있을까요?
그래프가 굉장히 크다면 어떤 탐색 기법을 고려해야 할까요? BFS
반대로, 그래프의 규모가 작고, depth가 얕다면 어떤 탐색 기법을 고려해야 할까요? DFS