알고리즘 study -20-

<문제 해결의 절차>

• 1. 문제를 정확히 이해한다
• 2. 문제를 해결하는 알고리즘을 설계한다
• 3. 알고리즘이 문제를 해결한다는 것을 증명한다(수학적으로)
• 4. 알고리즘이 제한시간 내에 동작한다는 것을 보인다(시간복잡도)
• 5. 알고리즘을 코드로 작성한다(한번에 디버깅 없이 한번에 하는 습관)

---

<문제해결의 기본 : 탐색공간 파악하기>

• 문제해결을 위해 고려해야 하는 모든 경우

---

ex> 연속 부분 최대합

• 연속된 부분을 선택하여, 그 합이 최대가 되게 하라(단, 1<=n<=100)
  

Q) 고려해야 하는 경우의 개수는?
-> 1개선택 = 8개 / 2개 선택 = 7개 ..... 8개 선택 = 1개
==>> n(n+1)/2 -> O(n^2)

Sol) 위 방법은 가능한 모든 경우를 고려했으므로 정답을 찾을 수 있다

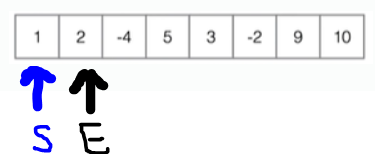
for(start = 0 ~ n)   -> O(n)
	for(end = start ~ n)   -> O(n)
    		for(start ~ end)  -> O(n)
        		sum 구하고 최대값 비교  -> O(1)

==>> O(n^3) 시간복잡도

---

<구현>

#include <stdio.h>
using namespace std;

const int MAX = 100;

int n;
int data[MAX];

int main() {

  scanf("%d", &n);
  
  for(int i = 0; i<n; i++)
    scanf("%d", &data[i]);
  
  int max = -999999999;
  for(int start = 0; start < n; start++){
    for(int end = start; end < n; end++){
      int sum = 0;
      
      for(int k = start; k<=end; k++){
        sum += data[k];
      }
      
      if(sum > max)
        max = sum;
    }
  }
  
  printf("%d\n", max);

  return 0;
}

---

n의 범위가 100 이상으로 주어지면 위 알고리즘은 비효율적!

for(start = 0 ~ n)   -> O(n)
	for(end = start ~ n)   -> O(n)
    		for(start ~ end)  -> O(n)
        		sum 구하고 최대값 비교  -> O(1)

위 부분에서 어떤 부분의 시간복잡도를 줄일 수 있을까???

-> start~end 구간 합을 구하는 과정을 재설계!

sol) [0][0~1] [0~2] ... [0~6][0~7]
위와 같이 처음 인덱스 부터 개수를 한 개씩 늘린 합을 원소로 하는 배열 생성

위 배열을 활용하여 start ~ end 합을 구할때 for문 사용하지 않고 계산

ex> start~end = (0~end) - {0~(start-1)}

---

#include <stdio.h>
using namespace std;

const int MAX = 100;

int n;
int data[MAX];
int sumFirst[MAX]; // sum[x] = 첫번째 숫자부터 x번째 숫자까지의 합

int main() {

  scanf("%d", &n);
  
  for(int i = 0; i<n; i++)
    scanf("%d", &data[i]);
  
  // 첫번째 숫자부터 x번째 숫자까지의 합 배열 구하기
  sumFirst[0] = data[0];
  for(int i = 1; i < n; i++)
    sumFirst[i] = sumFirst[i-1] + data[i];
//////////////////////////////////////////////
  
  int max = -999999999;
  for(int start = 0; start < n; start++){
    for(int end = start; end < n; end++){
      int sum = 0;
      
      if(start == 0)   // 처음부터 더하는 경우
        sum = sumFirst[end];
      else
        sum = sumFirst[end] - sumFirst[start-1];
      
      if(sum > max)
        max = sum;
    }
  }
  
  printf("%d\n", max);

  return 0;
}

---

문제 해결 시 우선 완전 탐색으로 생각해보자

-> 탐색공간을 파악하는 것이 문제 해결에서 가장 중요!
-> 모든 경우를 고려해서 시간 내에 해결이 된다면 ok
-> 시간 내에 해결이 되지 않으면 경우의 수를 줄이는 시도를 해야함