알고리즘 study -21-

<분할정복(Divide & Conquer)>

• 문제를 소문제로 분할
• 각각의 소문제를 해결
• 소문제의 해결 결과를 이용하여 전체 문제를 해결

---

<합병정렬>

• 재귀호출을 이용한 대표적인 정렬

-->> 처음에 mid = (start+end)/2로 나누는 것이 divide

---

앞 글에서의 <연속부분 최대합 문제> 를 분할정복으로 풀어보자

배열을 반으로 나누어 생각했을 때

• 최대합이 왼쪽에만 있는 경우
• 오른쪽에만 있는 경우
• 반으로 자린 자리를 포함해서 걸치는 경우

세 가지 경우로 나누어 생각을 해볼 수 있다

---

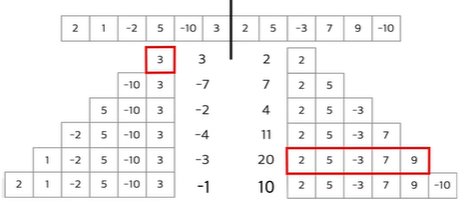
자른부분을 포함하는 경우 위 그림과 같이 왼쪽 오른쪽 각각 경우에서 최대를 더한 것을 찾아야 한다
ex> 위 그림의 경우 3 2 5 -3 7 9 가 자른 부분을 포함하는 경우에서 최대값이 된다

---

T(n) = n개의 숫자 중에 연속 부분 최대합을 구하는데 걸리는 시간
--> T(n) = 2*T(n/2) + O(n)

• 반으로 나눈 양쪽의 두 부분에서 연속 부분 최대합을 구하므로 2*T(n/2)
• 반으로 나눈 부분을 포함하는 경우 차례로 더하며 최대값을 찾아야하므로 O(n)

---

위 식을 정리하면 합병정렬과 같이 O(nlogn)의 시간복잡도를 가진다

#include <stdio.h>
using namespace std;

const int MAX = 100;

int n; // 숫자 개수
int data[MAX];

// 재귀함수를 작성하기 위한 과정
// 1. 함수를 말로 정의한다
// 2. 기저조건일 때 제대로 동작하게 작성한다
// 3. 함수가 제대로 동작한다고 가정하고 완성한다

int getSubMax(int start, int end){
  // data배열의 start 부터 end 까지 최대합을 구해주는 함수

  if(start >= end)  // 안전하게 하기 위해 >=
    return data[start];  // 원소가 하나이면 자기자신 리턴
  else{
    int mid = (start+end)/2;
    
    int left = getSubMax(start, mid); // 왼쪽 연속 부분 최대합
    int right = getSubMax(mid+1, end); // 오른쪽 연속 부분 최대합
    
    // 중간 부분을 포함하는 연속부분 중 최대합 구하기
    
    int leftSum = 0;
    int leftMax = -99999999;
    for(int i=mid; i>=start; i--){
      leftSum += data[i];
      
      if(leftMax < leftSum)
        leftMax = leftSum;
    }
    
    int rightSum = 0;
    int rightMax = -99999999;
    for(int i=mid+1; i<=end; i++){
      rightSum += data[i];
      
      if(rightMax < rightSum)
        rightMax = rightSum;
    }
    
    int middleMax = leftMax + rightMax;
    
    // 세개의 값 비교
    if(left >= right && left > middleMax) return left;
    else if(right >= left && right >= middleMax) return right;
    else return middleMax;
    
  }
}

int main() {

  scanf("%d", &n);
  
  for(int i = 0; i<n; i++)
    scanf("%d", &data[i]);
    
  printf("%d\n", getSubMax(0, n-1));

  return 0;
}

---