알고리즘 study -23-

<연속 부분 최대합 문제를 동적계획법으로 풀이>

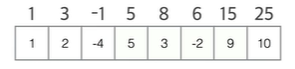
각 원소가 오른쪽 끝에 있다 가정했을 때 최대값들을 나열한 것이다
ex> -4의 경우 -4 vs 2 - 4 vs 1 + 2 - 4 --> -1이 최대!

n번째를 오른쪽 끝으로 했을 때 연속 부분 최대합은 n-1번째를 오른쪽으로 끝으로 하는 연속 부분 최대합을 이용하면 된다!!

---

<풀이 순서 적용>

• 1. 부분 문제 정의 = 무슨 값을 구할지를 정의
     -> T(i) = i번째 숫자를 오른쪽 끝으로 하는 연속 부분 최대합
     T(i) = max(T(i-1) + Data[i], Data[i])
     
     그 전 원소를 오른쪽 끝으로 했을때의 최대합에 현재 원소 더한 것 vs 현재 원소 하나의 값

---

#include <stdio.h>

using namespace std;

const int MAX = 100;

int Table[MAX];  // 최대값들 들어갈 배열
int Data[MAX]; // data 배열
int n; // 원소 개수

int main() {
  
  scanf("%d", &n);
  
  for(int i = 0; i<n;i ++)
    scanf("%d", &Data[i]);
  
  
  // 기저 조건은 직접 채워주자 / 점화식으로 채우지 못하므로
  Table[0] = Data[0];
  
  for(int i = 1; i<n; i++){
    if(Table[i-1] + Data[i] > Data[i])
      Table[i] = Table[i-1] + Data[i];
    else
      Table[i] = Data[i];
  }
  
  int myMax = -999999999;
  
  for(int i = 0; i<n; i++){
    if(Table[i] > myMax)
      myMax = Table[i];
  }
  
  printf("%d\n", myMax);
  

  return 0;
}

---

<팰린드롬 만들기> - 동적계획법 사용

• palindrome = 앞으로 읽거나 뒤로 읽거나 모두 같은 문자열

Q. 팰린드롬을 만들기 위한 최소 추가 문자 개수를 구하여라
ex> abccdbac -> 2 // a왼쪽에 c, b오른쪽에 d 넣으면 팰린드롬

---

• 1. T(i,j) = i부터j까지 문자열을 palindrome으로 만들기 위해 추가해야 하는 문자개수 최솟값

양 끝 문자가 같다면 T(i,j) = T(i+1, j-1)
다르다면 T(i,j) = min(T(i+1,j) + 1, T(i, j-1) + 1)
(왼쪽 끝을 오른쪽 끝의 오른쪽에 붙이기 or 오른쪽 끝을 왼쪽 끝의 왼쪽 끝에 붙이기)

---

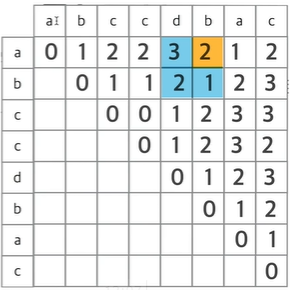
• T(i+1, j-1) = 왼쪽 아래 대각선
• T(i, j-1) = 왼쪽
• T(i+1, j) = 아래쪽

---

#include <stdio.h>
#include <string.h>

int const MAX = 1010;

char data[MAX];
int Table[MAX][MAX] = {0,};

int main() {

  scanf("%s", data); // 문자열 입력
  
  int len = strlen(data);
  
  for(int i = len-2; i >= 0; i--){
    for(int j = i+1; j <= len-1; j++){
      if(data[i] == data[j])
        Table[i][j] = Table[i+1][j-1];
      else{
        if(Table[i+1][j] < Table[i][j-1])
          Table[i][j] = Table[i+1][j] + 1;
        else
          Table[i][j] = Table[i][j-1] + 1;
      }
    }
  }
  
  printf("%d\n", Table[0][len-1]);
  

  return 0;
}

---

<동적계획법 정리>

• 부분문제를 정의하는 것이 가장 어렵다
  -> 어떻게 정의하느냐에 따라 풀리기도 하고 안풀리기도 함

• 문제가 "재귀적으로 해결되는지"를 볼 줄 알아야 함
  -> 규칙찾는 것으로 보일 때도 있고, 실제로 틀린 말도 아니다

• 많은 예제를 풀어야 익숙해질 듯 하다
  -> 재귀호출 & 동적계획법 기초 실력 향상은 우선 많은 문제를 접해봐야 한다

---