알고리즘 study -22-

<동적 계획법>

-> 부분 문제를 해결한 결과를 이용하여 전체 문제를 해결

---

<동적계획법과 분할정복법의 차이>

• 분할정복법 : 위에서 밑으로 큰 문제를 쪼개면서 내려간다
• 동적계획법 : 제일 작은 것 부터 하나하나 구해서 제일 큰 문제를 해결

---

<동적 계획법의 문제 풀이 순서>

• 1. 부분 문제를 말로 정의한다 = 무슨 값을 구할지를 정의(함수 정의)
     -> T(i) 정의하기!!
• 2. 점화식을 구한다 = 그 값을 어떻게 구할지에 대한 식 세우기
     -> 부분문제 or 소문제는 풀려있다고 가정!
• 3. 점화식을 바탕으로 문제를 해결한다 = 값을 직접 구하는 코드 작성

ex> 피보나치 수열을 동적계획법으로 풀이

---

ex>
2 X N 상자를 2 X 1 블럭으로 채우는 경우의 수??

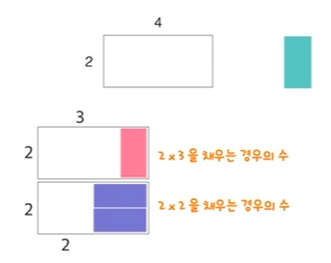
--> 2x4를 채우는 경우 마지막이 세워져 있는 것과 눕혀있는 두 가지 경우로 나눌 수 있다

• 1. T(i) = 2 x i의 상자를 채우는 경우의 수
• 2. 점화식 : 2 x i = 2 x (i-1) + 2 x (i-2)
     -->> T(i) = T(i-1) + T(i-2) = 결국 피보나치 수열 문제!!!

  

  ---

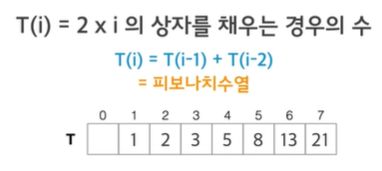
  전체 경우를 어떻게 나눠서 바라 볼것인지 중요!!
  나눠서 합쳐서 완성하는 방법 찾아보기

  ---

<숫자 만들기>

동적계획법 대표적 예제

---

1~M 까지의 숫자를 더하여 N을 만드는 경우의 수는???

ex> 입력 : 5(N) 3(M) // 출력 : 13

--> 맨 끝이 1로 끝나는 경우 / 2로 끝나는 경우 / 3으로 끝나는 경우

--> 1. 부분문제 정의 : T(i) = 1~M의 수를 이용하여 i를 만드는 경우의 수
2. 점화식 : T(i) = T(i-1) + T(i-2) + ... + T(i-M)
3. 문제해결 :

#include <stdio.h>
using namespace std;

const int MAX = 100;

int Table[MAX];
int n, m;

int main() {

  scanf("%d %d", &n, &m);
  
  // ex> M = 4;
  // Table[1] = 1
  // Table[2] = 2
  // Table[3] = Table[1] + Table[2] + 1  // 3 하나만 있는 경우
  // Table[4] = Table[3] + Table[2] + Table[1] + 1
  
  // 1-M 까지 구하기
 Table[1] = 1;
 int sum = 0;
 
 for(int i = 2; i <= m; i++){
   sum += Table[i-1];
   
   Table[i] = sum + 1;
 }
 
 for(int i = m+1; i <=n; i++){
   for(int j=i-m; j<=i-1; j++ ){
     Table[i] += Table[j];
   }
 }
 
 printf("%d\n", Table[n]);
 
  return 0;
}

---