Graph
제일 복잡한 형태의 일반화된 자료구조
G = (V, E)
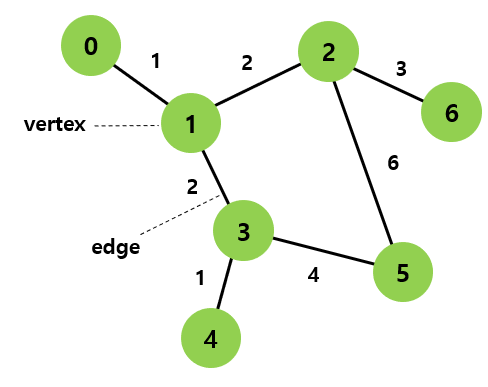
# V = vertex set : 각각의 노드들에 대한 정보 (vertex,node,정점,노드)
# E = edge set : 노드 사이의 관계(edge)에 대한 정보(두 노드의 값으로 한개의 edge를 표현한다)
V = {0,1,2,3,4,5,6}
E = {(0,1),(1,2),(1,3),...,(6,2)}
Graph 관련 용어
- 정점(vertex): 위치라는 개념. (node 라고도 부름)
- 간선(edge): 위치 간의 관계. 즉, 노드를 연결하는 선 (link, branch 라고도 부름)
- 인접 정점(adjacent vertex): 간선에 의해 직접 연결된 정점
- 정점의 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 무방향 그래프에 존재하는 정점의 모든 차수의 합 = 그래프의 간선 수의 2배- 전체 그래프의 차수는 각 노드의 차수 중 최대값이 된다.
- 진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (내차수 라고도 부름)
- 진출 차수(out-degree): 방향 그래픙에서 외부로 향하는 간선의 수 (외차수 라고도 부름)
- 방향 그래프에 있는 정점의 진입 차수 또는 진출 차수의 합 = 방향 그래프의 간선의 수(내차수 + 외차수) - 경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
- 단순 경로(simple path): 경로 중에서 반복되는 정점이 없는 경우
- 사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우, 닫힌 경로
사이클이 없는 그래프 = Tree (사이클이 없으면 두 노드를 잇는 경로는 한가지 방법 뿐이다.)
출처 : https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
- graph는 무방향과 방향 두가지의 간선 종류를 갖는다.
- 무방향 그래프는 두 노드사이가 서로를 향할 수 있다.
- 방향 그래프는 두 노드사이에 특정 방향으로만 경로가 성립한다.

Graph의 표현
그래프는 인접행렬과 인접리스트로 표현할 수 있다.
- 인접행렬은 다음과 같이 표현할 수 있다.
0,0 ~ 5,5 의 대각선방향의 인덱스는 자기자신을 향하는 경로로 자기자신으로의 loop가 가능하거나, 가능하지 않거나는 문제 정의에 따라서 바뀔 수 있다.G = [ [1,1,0,0,1,0], [1,1,1,0,1,0], [0,1,1,1,0,0], [0,0,1,1,1,1], [1,1,0,1,1,0], [0,0,0,1,0,1] ]
인접 행렬은 실제 간선 정보에 비해서 쓰이지 않는 데이터도 자릿값을 차지하기 때문에 메모리의 낭비가 심하다.
만약 각 노드에 가중치가 있다면 1이 아닌 가중치에 대한 값을 주게되면 가중치 사용이 가능하게된다.
- 인접리스트는 엣지(간선)의 정보만을 표현한다.
G
[1]->[2 | ]->[1 | ]->[5 | ]->none
[2]->[2 | ]->[5 | ]->[1 | ]->[3 | ]->none
[3]->[3 | ]->[2 | ]->[4 | ]->none
[4]->[5 | ]->[4 | ]->[3 | ]->[6 | ]->none
[5]->[1 | ]->[2 | ]->[4 | ]->[5 | ]->none
[6]->[6 | ]->[4 | ]->none
각각이 노드의 연결, 즉 엣지를 표현한다. (self-loop)를 표현한다.
각 리스트를 한 방향 또는 양 방향으로 표현할 수 있다. 리스트의 순서, 정렬은 상관없다.
방향이 있는 그래프는 각 방향에 맞춰서 연결 리스트를 만들어준다.
인접리스트에서도 각 표현에서 가중치를 표현해주면 된다.
| 인접행렬 | 인접리스트 | |
|---|---|---|
| memory | O(n^2) | O(n) -> O(n+m) |
| search | O(1) -> (G[u][v]==1) | O(n) -> (G[u].search(v)) |
| u에 인접한 모든 노드 v 에 대해 | O(n) -> (for 문 (1,n+1)범위의 v에 대해 G[u][v]를 조작) | O(인접노드수) -> 각 edge(node)에 대해서만 for문으로 조작 |
| 새 에지 삽입(u,v) | O(1) -> G[u][v] = 1 | O(1) -> G[u].pushFront(v) (python에서는 append) |
| 에지 삭제(u,v) | O(1) -> G[u][v] = 0 | O(n) -> G[u]를 서치 후, 그 노드를 삭제 |
각 노드사이에 에지개수가 많으면 인접 리스트도 n^2으로 메모리가 수렴하지만,
일반적인 경우에는 메모리 측면에서 행렬에 비해서 메모리 사용에 유리하다.
대신 탐색이나 연산을 할 때 상대적으로 불리하다.
Graph 순회
이진 트리의 preorder, inorder, postorder와 같은 탐색 방법이 필요하다.
-> DFS(깊이 우선 탐색), BFS(너비 우선 탐색)
DFS (recursive)
curr_time = 1 # 초기화
DFS(v): # v를 방문 중
mark[v] = 'visited'
pre[v] = curr_time # v의 첫번째 방문 시간
curr_time += 1
for each edge(v,w): # v에 인접한 모든 노드 w에 대해
if mark[w]!='visited'
parent[w] = v
DFS(w)
# v에 인접한 모든 노드를 고려하면 for loop 탈출
post[v] = curr_time # v에서 DFS가 완료된 시간
curr_time += 1
return
DFSAll(G): # 연결되지 않은 형태의 DFS일 때,
for all nodes v in G:
mark[v] = 'unvisited'
for all nodes v in G:
if mark[v] != 'visited'
DFS(v)DFS (stack)
DSF(s):
stack.push((None,s)) # tuple의 형태로 삽입
while stack is not empty:
p,v = stack.pop()
if v is unmarked:
mark[v] = 'visited'
parent[v] = p
for each edge (v,w):
if w is unmarked:
stack.push((v,w))