
📌 슬라이딩 윈도우 알고리즘(Sliding Window)
슬라이딩 윈도우 알고리즘을 쉽게 비유하자면, 어떤 창문을 왼쪽부터 오른쪽으로 밀어 오면서 창문 안에 있는 값들을 부분 배열이라고 생각하는 것과 같습니다.
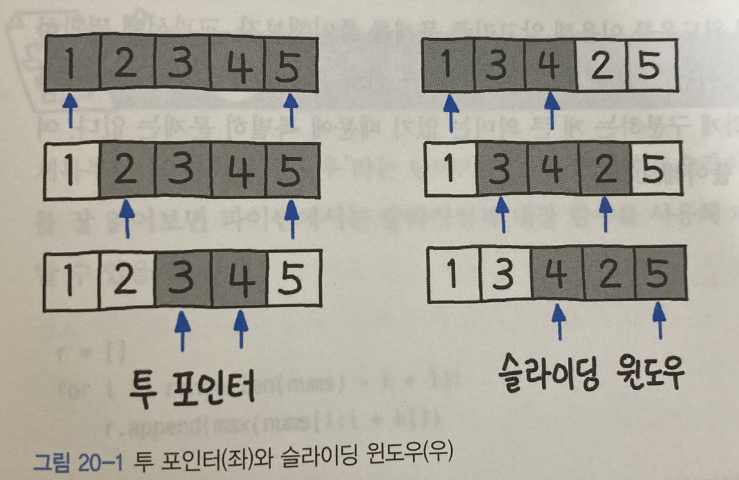
슬라이딩 윈도우 알고리즘은 연속되는 투 포인터와 유사하게 부분 배열들을 활용하여 특정 조건을 일치시키는 알고리즘이지만, 부분 배열의 길이(크기)가 고정적 입니다.
- 선형 공간(1차원 배열)을 2회 이상 반복적으로 탐색해야 할 경우 O(N^2) 이상 걸릴 시간 복잡도를 부분 배열을 활용하여 O(N)으로 줄일 수 있다는 공통점을 가지고 있습니다.
위 이미지를 참고해서 보면, 투 포인터 알고리즘은 구간의 넓이가 조건에 따라 유동적으로 변하지만 슬라이딩 윈도우 알고리즘은 항상 구간의 넓이가 고정되어 있다는 차이점을 가지고 있는 것을 확인할 수 있습니다.
즉, 고정 사이즈의 윈도우가 이동하면서 윈도우 내에 있는 데이터를 이용해 문제를 풀이하는 알고리즘입니다.
교집합의 정보를 공유하고, 차이가 나는 양쪽 끝 원소만 갱신하는 방법을 통해 배열이나 리스트의 요소의 일정 범위의 값을 비교할 때 사용하면 매우 유용합니다.
슬라이딩 윈도우 알고리즘은 투 포인터(two pointers)알고리즘과 연동하여 많이 쓰입니다.
- 투 포인터(two pointers)알고리즘 : 1차원 배열이 있고, 이 배열에서 각자 다른 원소를 가리키는 2개의 포인터를 조작하며 원하는 값을 얻는 형태의 알고리즘
투 포인터 알고리즘은 부분 배열의 길이가 가변적 이기 때문에 부분 배열의 구간을 정할 2개의 포인터 변수가 필요한 반면, 슬라이딩 윈도우 알고리즘은 부분 배열의 길이를 고정적으로 잡기 때문에 포인터 변수가 2개일 필요가 없습니다.
즉, 고정적인 부분 배열의 크기를 나타내는 변수가 있다면 포인터 하나만 있어도 부분 배열의 크기를 알고 있기 때문에 각 배열의 끝이 어딘지 알 수 있습니다.
📌 관련 문제 풀이

슬라이딩 알고리즘에서 사용되는 N과 W는 모두 고정된 상수입니다.

예를들어, 8개의 숫자가 있는 배열이 존재하고 넓이가 3인 창문이 있다고 가정했을때 제일 왼쪽에 배치시켜서 왼쪽부터 한 칸씩 오른쪽으로 이동하는 방식으로 슬라이딩 알고리즘을 적용하여 창문의 범위에 해당하는 부분들의 구간합 등을 만들어 낼 수 있습니다.
인프런 알고리즘-최대매출

const n = 10; // N일 - 배열의 길이
const k = 3; // W 창문의 넓이
const arr = [12, 15, 11, 20, 25, 10, 20, 19, 13, 15]; // 1차원 고정배열
function solution(n, k, arr) {
let result = 0; // 길이 k의 부분 수열의 요소 전체 합의 최댓값
let sum = 0; // 특정 부분 수열의 전체 합
// 배열의 가장 왼쪽부터 k까지의 값의 합을 sum에 담음
for (let i = 0; i < k; i++) {
sum += arr[i];
}
result = sum;
// k는 고정적이므로 새롭게 갱신되는 arr[i]와 기존 arr[i - k]를 빼줌
for (let i = k; i < arr.length; i++) {
sum += arr[i] - arr[i - k];
// 최대 합을 비교해서 갱신
result = Math.max(result, sum);
}
return result;
}
console.log(solution(n, k, arr));
n이 3 이상일 때 가능한 타일 배치는( d[n] : 가로의 길이가 n일 때 배치 가능한 타일의 수 )d[3] = d[2] + d[1]로 표현할 수 있다.따라서 점화식은 아래와 같이 표현할 수 있습니다.
d[n] = d[n-1] + d[n-2]2x1개를 채우는데는 1개, 2x2을 채우는데는 2개, 2x3을 채우는데는 3개, 2x4를 채우는데는 5개, 2x5를 채우는데는 8개 이런식으로, 1, 2, 3, 5, 8, 13... 과 같이 피보나치 패턴으로 구해진다는 것을 알 수 있습니다.
10007로 나누지 않고 마지막에 arr에 넣은 값을 10007로 나눠서 출력하면 값이 너무 커져서 컴퓨터 내부에서 정상적인 계산이 이루어지지 않기 때문에 주의해야합니다.
const fs = require('fs');
let input = Number(fs.readFileSync('/dev/stdin').toString().trim());
let arr = [0, 1, 2];
for (let i = 3; i <= input; i++) {
arr[i] = (arr[i-1] + arr[i-2]) % 10007;
}
console.log(arr[input]);