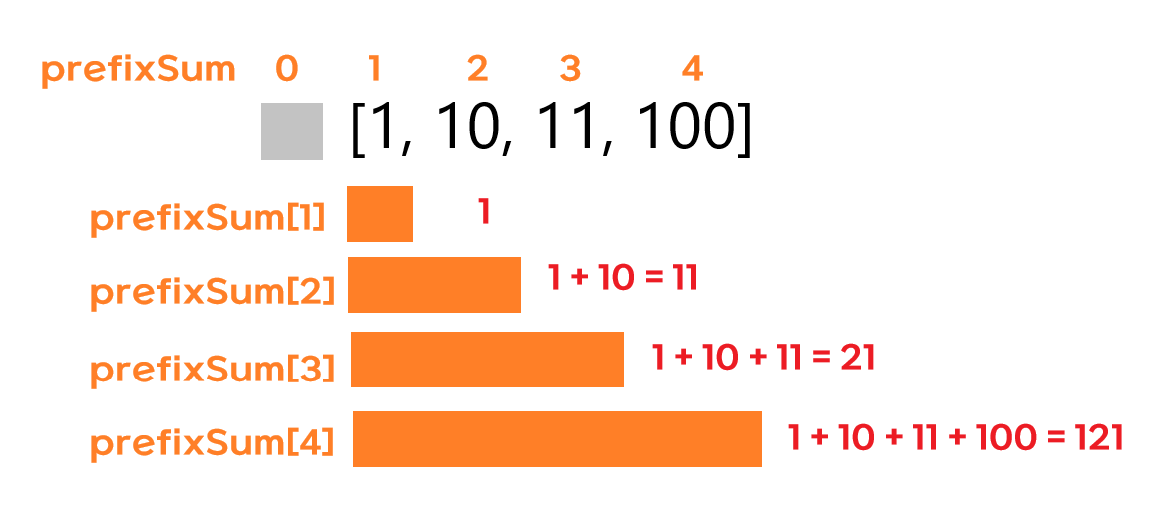누적합
누적합이란?
요소들의 누적된 합의 의미
어떠한 배열을 기반으로 앞에서부터 요소들의 누적된 합을 저장해 새로이 배열을 만들어서 이를 활용하는 것을 말한다.
흔히, 앞에서부터 더하는 prefix sum 과 뒤에서부터 더하는 suffix sum이 있다.
코딩테스트에는 주로 prefix sum이 대체적으로 많이 나오는 추세이다.
누적합을 만들땐 0번째에는 아무값도 담지 않고, 1번째부터 담아야한다.
보통 배열을 만들땐 0번째부터 시작하지만 prefix sum을 만들땐, 1번째부터 배열을 담아놔야 만들기가 쉽다.
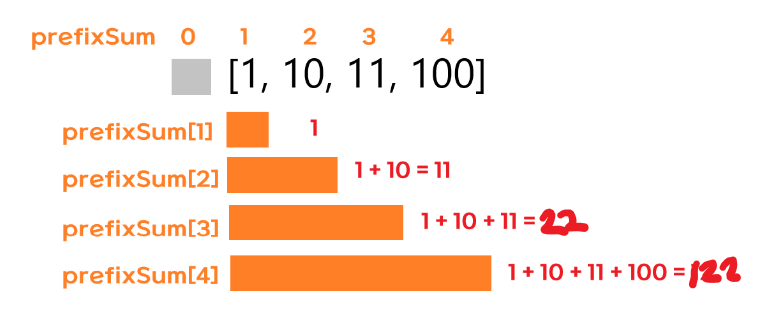
let arr = [1, 10, 11, 100];
//0번째 x, 첫번째 1, 두번째10, 세번째11, 네번째100prefix sum의 첫번째 요소는 arr의 첫번째 1 합한것, -> 1 = 1
두번째는 arr의 두번째 10까지 합한것, -> 1 + 10 = 11
세번째는 11까지 합한것, -> 1 + 10 + 11 = 21
네번째는 100까지 합한것 -> 1 + 10 + 11 + 100 = 121
앞에서부터 더한 것을 기반으로 배열을 만든다.
이렇게 더한 것을 어떠한 연산에 활용할 수 가 있다는 것이다.
누적합 예시문제
승철이는 뇌를 잃어버렸다. 학교에 갔더니 선생님이 자연수로 이루어진 N개의 카드를 주며 M개의 질문을 던진다. 그 질문은 나열한 카드중 A번째부터 B번째까지의 합을 구하는 것이다. 뇌를 잃어버렸기 때문에 승철이는 이 문제를 풀 수 없다. 문제를 풀 수 있는 프로그램을 작성해보자.
입력:
수의 개수 N, 합을 구해야 하는 횟수 M,
그 이후 N개의 수가 주어진다. 수는 100이하의 자연수.
그 이후 M개의 줄에는 합을 구해야 하는 구간 A, B가 주어진다.
출력:
M개의 줄에 A부터 B까지의 합을 구하라.
범위:
1 <= N <= 100,000
1 <= M <= 100,000
1 <= A <= B <= N
예제입력:
8 3
1 2 3 4 5 6 7 8
1 4
1 5
3 5예제출력:
10
15
12일차원 배열에서의 예제문제 풀이

이 예제문제는 구간합쿼리 문제이다.
특정한 구간을 정해 합이나 곱이나 어떠한 연산을 해서 구간에 대한 쿼리를 날리는 것을 구간쿼리 라고 한다.
1부터 5까지의 수를 누적합을 사용하여 psum이라는 배열을 만들었다고 가정해보자.
psum의 요소는 아래와 같을 것이다.
let psum = [1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5]
//[1, 3, 5, 10, 15]만약 요구사항에서 2부터 5까지의 합을 구하라 했다면,
이 구간의 합은 psum의 5번째요소 -psum 1번째요소 일 것이다.
psum = [1, 3, 6, 10, 15];
//15 - 1 = 14;
//2+3+4+5 = 14;만약 요구사항에서 2부터 3까지의 합을 구하라 했다고 해도,
3번째요소 - 1번째요소를 한 결과값과 같은 값이 나온다.
//6 - 1 = 5;
//2 + 3 = 5;누적합을 사용하면 매번 구간쿼리가 왔을때, 더할 필요없이 단순하게 - 연산만으로 문제 해결이 가능해진다.
누적합을 사용할 수 있는 배열이란?
배열의 요소가 정적인 배열에만 누적합을 사용할 수 있다.
요소가 변하지 않는 정적배열이라면 누적합을 사용할 수 있다.
구간쿼리 문제를 풀 때 2가지 알고리즘을 떠올릴 수 있어야 한다.
첫번째는 누적합과 두번째는 펜윅트리이다.
하지만, 배열의 요소가 중간에 바뀐다거나 동적배열인 경우엔 누적합 사용이 불가능하기 때문에 펜윅트리라는 알고리즘을 사용해야 한다.
누적합의 시간복잡도
누적합은 O(1)의 시간복잡도를 가진다.
누적합은 큰 시간복잡도를 줄일 수 있다.
만약 n을 10만번 반복하고, m을 10만번 반복하는 코드를 작성했다면
그 코드의 시간복잡도는 100억이 된다.
하지만, 누적합으로 간단한 - 만을 사용하여 풀게 된다면 O(1)의 상수시간 시간복잡도를 가진다.
따라서, 10만 * 10만이 아니라 10만 곱하기 1로 줄일 수 있다.
누적합을 만드는 방법
누적합을 만들땐, 첫번째 요소의 값으로 배열의 첫번째 합을 받기때문에
1부터 시작해야한다. 만약 i가 0부터 시작하게 된다면 배열의 인덱스가 0부터 시작하기 때문에 참조할 수 없는 오류가 발생한다.
//예시
for(let i = 1; i <= n; i++) {
psum[i] = psum[i - 1] + arr[i];
}
for(let i = 0; i < m; i++) {
count = psum[c] - psum[b - 1]
}
return 0;만들때마다 더해서 만드는 방법도 있지만, 더 효율적인 방법이 있다.
psum첫번째 요소를 기반으로 psum의 두번째요소는 psum첫번째요소 + arr의 현재요소값을 요소로 가지게 된다.
마찬가지로,
psum[3]은 psum[2] + arr[3]을 더한 값 이러한 순환 과정을 이해하고 코드로 만들어보면 쉽게 누적합을 구현할 수 있게 된다.
참고 자료
https://www.youtube.com/watch?v=906Kko5nZhE
https://jindory.tistory.com/m/entry/Javascript-%EB%B0%B0%EC%97%B4-%EB%88%84%EC%A0%81%EA%B0%92-%EB%A7%8C%EB%93%A4%EA%B8%B0