📌 정렬 알고리즘
정렬 알고리즘이란?
특정 원소들을 번호순이나 사전 순서와 같이 일정한 순서대로 열거하는 알고리즘,
데이터를 기준에 맞게 순서대로 배열하는 작업
정렬 알고리즘이 중요한 이유
정렬 알고리즘은 컴퓨터 분야에서 중요시되는 문제 중 하나이며, 탐색에 용이한 특징을 가지고 있다.

정렬되지 않은 데이터에서 원하는 값을 찾아야 할 경우, 순차탐색과 이진탐색의 차이점을 통해서 알 수 있다.
- 만약 43억개 중 특정 값을 찾아야할 경우 순차탐색은 최악의 경우 43억번 탐색을 해야하지만 이진탐색의 경우 32회만으로 탐색이 가능해진다.
이렇듯 정렬 알고리즘은 프로그래밍과 알고리즘 이해에 많은 도움이 된다.
ex. for문 & if문, 재귀 분할정복, 힙 자료구조, 시간복잡도 등등
📌 버블 정렬(Bubble Sort)

- 인접한 두개의 요소를 비교해가면서 큰 값은 뒤로, 작은 값은 앞으로 보내면서 정렬을 진행
- 한번 돌때마다 마지막 요소가 정렬되는 것이 마치 거품이 올라오는 것처럼 보여서 버블 정렬이라고 부른다.
//버블 정렬 알고리즘 구현예시
function bubbleSort(arr) {
let noSwaps;
for (let i = arr.length; i > 0; i--) {
noSwaps = true;
for (let j = 0; j < i - 1; j++) {
if (arr[j] > arr[j + 1]) {
let temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
noSwaps = false;
}
}
if (noSwaps) break;
}
return arr;
}- i라는 변수를 통해 배열의 마지막 지점에서 시작지점까지 순회하는 반복문을 만듭니다. (전체범위 반복)
- j라는 변수를 통해 시작점부터 i - 1 까지 순회하는 이중 반복문을 만듭니다. (첫번째 요소부터 정렬해야하는 마지막 요소까지 반복)
- 배열의 j번째 요소가 j + 1번째 요소보다 크면, 두 개의 위치를 바꿉니다. (Swap - 순서가 맞지않으면 교환)
- 만약 Inner Loop 에서 Swap이 발생하지 않는다면, 모두 정렬된 것이므로 반복문을 종료합니다.
- 정렬된 요소를 return 합니다.
버블정렬 특징과 시간복잡도
- 장점: 구현이 매우 간단하다.
- 단점: 순서에 맞지 않는 요소들의 교환이 자주 일어난다.
(하나의 요소가 가장 왼쪽에서 가장 오른쪽으로 교환되어야 할 경우) - 시간 복잡도: 최악 O(n^2), 평균 O(n^2), 최선 O(n)//이미 정렬된 상태일 경우(굉장히 드물다.)
📌 선택 정렬(Selection Sort)

- 전체 범위에서 차례대로 가장 작은 숫자를 탐색하고, 가장 왼쪽부터 차례대로 교환하는 방식
- 전체 범위를 돌면서 작은 숫자를 선택하여 정렬하는 것
//선택 정렬 알고리즘 구현 예시
const selectionSort = (arr) => {
for (let i = 0; i < arr.length - 1; i++) {
let min = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
if (min !== i) {
[arr[i], arr[min]] = [arr[min], arr[i]];
}
}
return arr;
};- 먼저 전체범위를 반복하고 첫번째 요소를 min이라는 변수에 저장합니다.
- 반복문을 통해 min을 다음요소들과 비교하면서 가장 작은 값을 min에 할당합니다.
- 만약 min이 최초에 저장한 값이 아니라면, 두 값을 swap 합니다.(구조분해 할당)
- arr의 모든 요소에 위 작업을 반복한 후 정렬된 배열을 리턴합니다.
선택정렬 특징과 시간복잡도
- 장점: 자료 이동 횟수가 미리 결정된다.
(가장 왼쪽에서 가장 오른쪽으로 모든 요소를 교환하지 않아도 됨) - 단점: 값이 같은 요소가 있다면 상대적인 위치가 변경될 수 있다.
(안정성 우려 - 같은 1이여도 첫번째1과 두번째1이 바뀔 수 있다.) - 시간 복잡도: 최악 O(n^2), 평균 O(n^2), 최선 O(n^2)
(전체 요소를 반복하면서 매번 전체 요소를 한번씩 다시 돌기때문에 On제곱의 시간복잡도를 가짐)
📌 삽입 정렬(Insertion Sort)
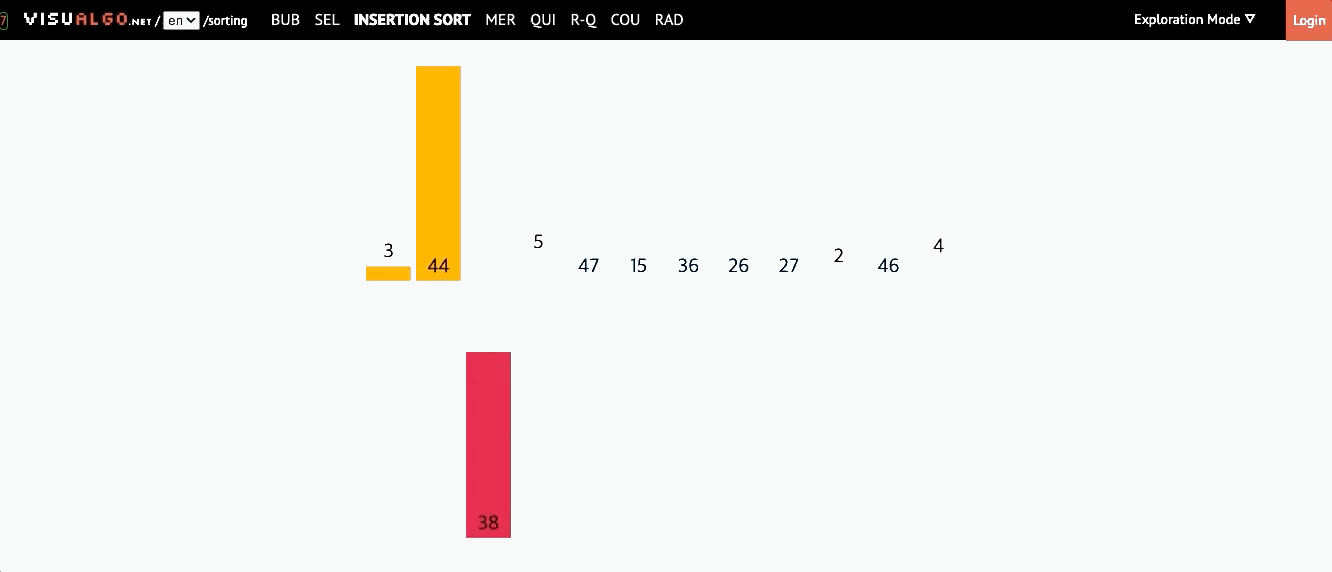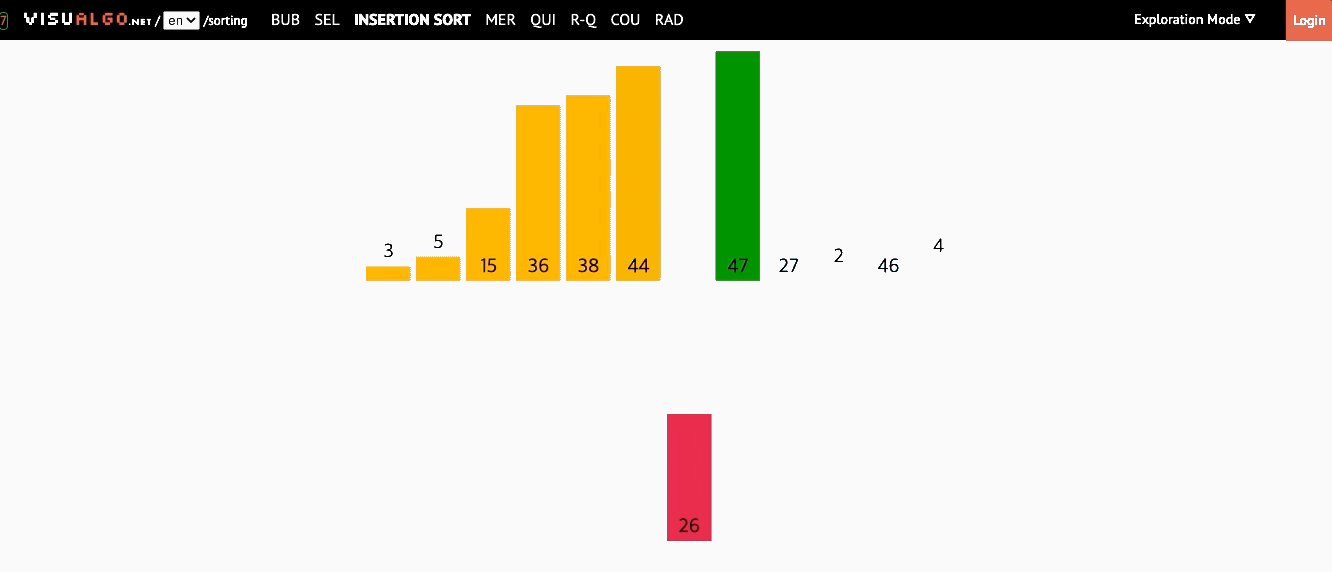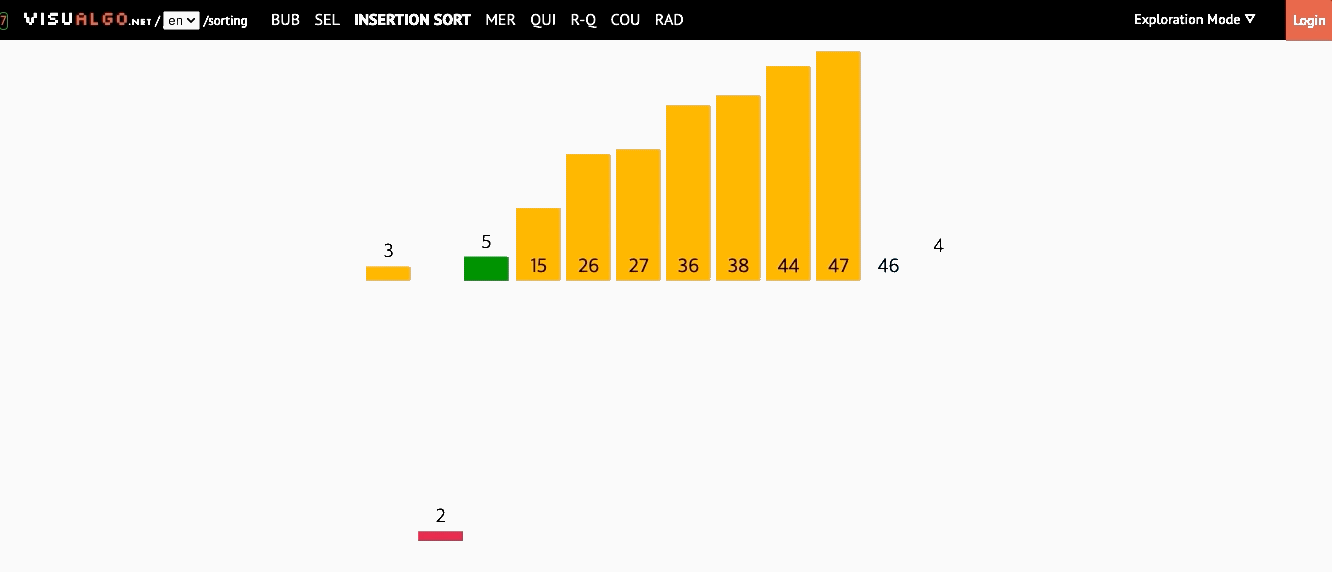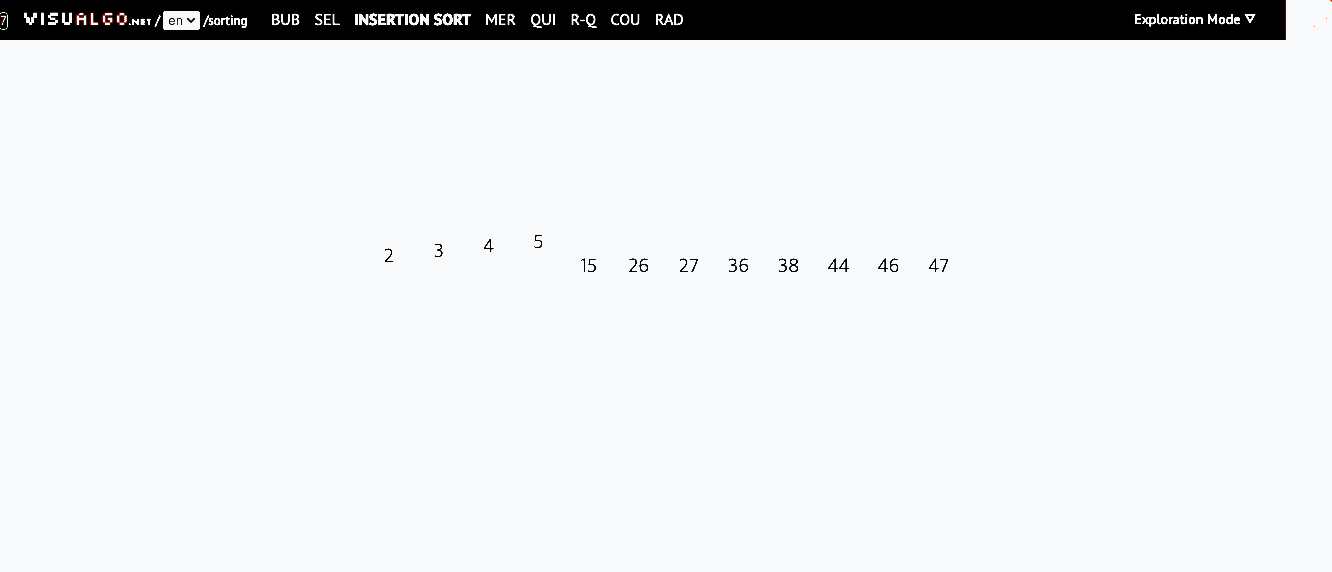
- 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열부분과 비교하여, 자신의 위치를 찾아 삽입하는 방식
- 이미 정렬된 배열에서 자기 자신의 위치를 찾아 삽입된다해서 삽입 정렬
function insertionSort(arr) {
for (let i = 1; i < arr.length; i++) {
let currentVal = arr[i];
let j;
for (j = i - 1; j >= 0 && arr[j] > currentVal; j--) {
arr[j + 1] = arr[j];
}
arr[j + 1] = currentVal;
}
return arr;
}- 먼저 전체범위를 반복한다.
- 아직 정렬되지 않은 배열에서 삽입될 i번째 정수를 변수에 저장한다.
- 이미 정렬된 부분부터 탐색하기 때문에 i - 1부터 삽입을 위한 위치 인덱스도 저장을 해준다.
- 이미 정렬된 배열에서 i번째 정수가 삽입될 위치를 탐색해 간다.
(이때 i번째 정수보다 큰 값이면 오른쪽으로 한칸씩 밀어준다. -교환작업) - 탐색이 완료되고 삽입될 위치에 i번째 정수를 삽입한다.
삽입정렬 특징과 시간복잡도
- 장점: 최선의 경우 O(n), 안정한 알고리즘, 이미 정렬이 많이 되어 있는 상황에서 유리하며 데이터 수가 적을수록 방식이 간단해서 유리하다.
- 단점: 요소가 너무 많으면 비교적 많은 이동을 해야하므로 성능이 좋지 않다.(삽입하려면 그 뒤에 있는 데이터들을 전부 밀어야하기 때문에 이동이 많이 발생한다.) //효율적이지는 못한 알고리즘
- 시간 복잡도: 최악 O(n^2), 평균 O(n^2), 최선 O(n)//이미 모든 데이터가 정렬되어 있는 경우
📌 병합 정렬(Merge Sort)
위에서 설명했던 정렬들보다 조금 더 효율적이지만 복잡한 정렬에 대해 알아보자.
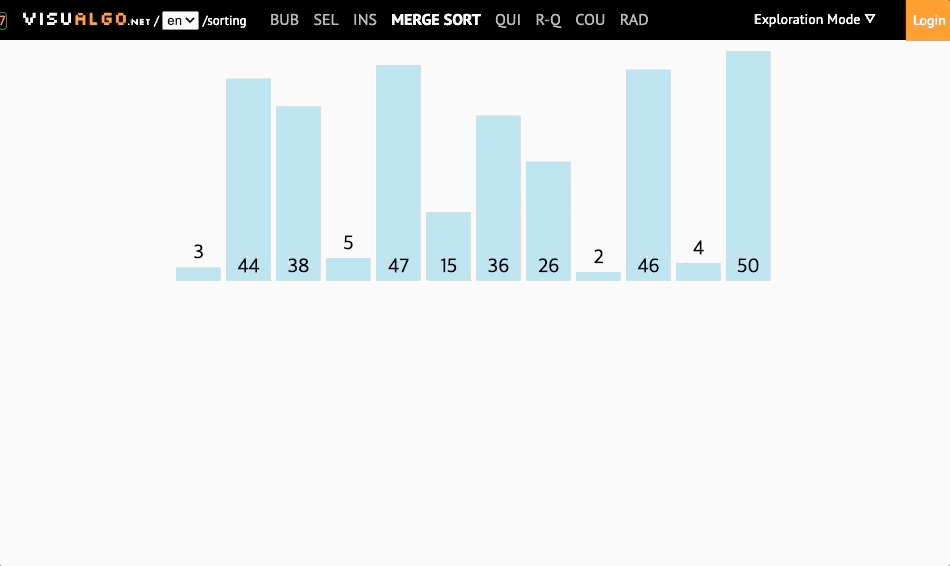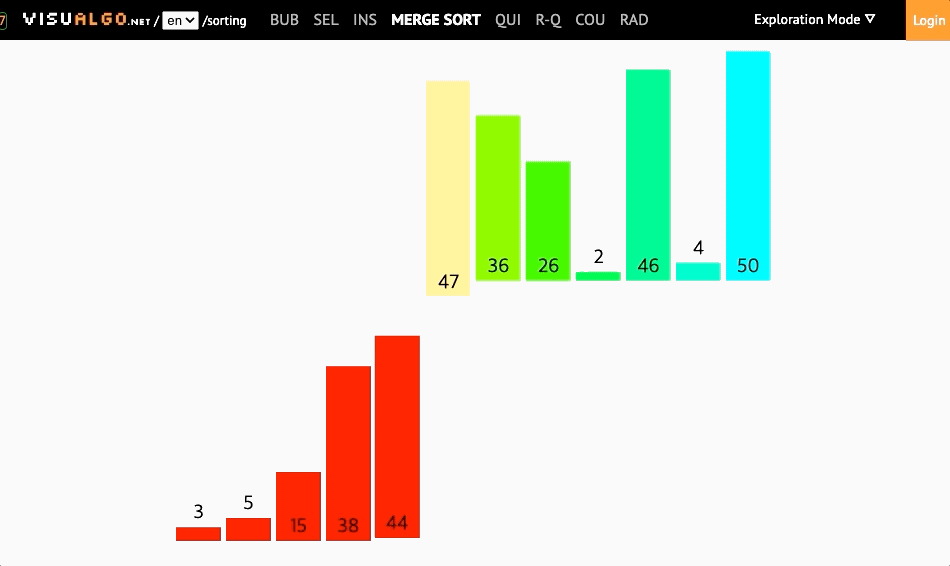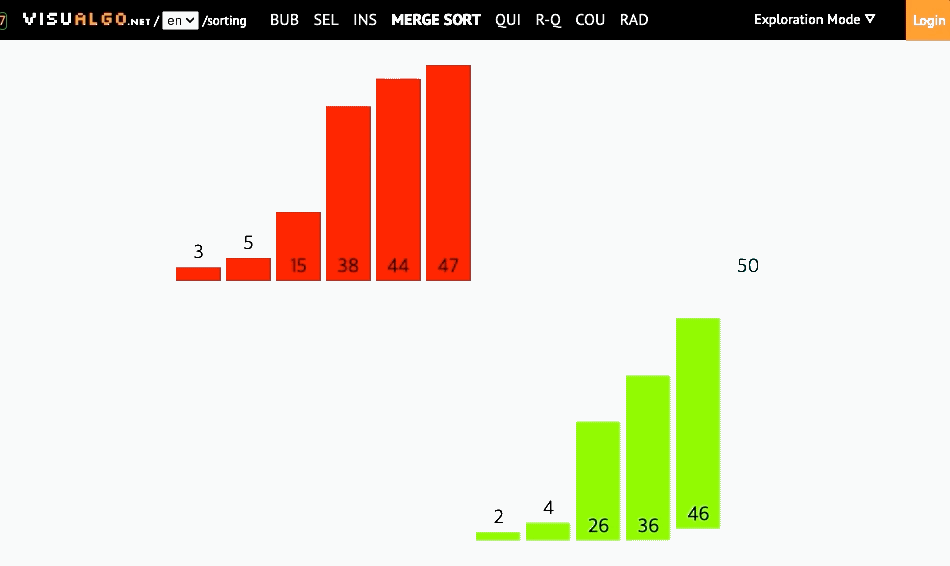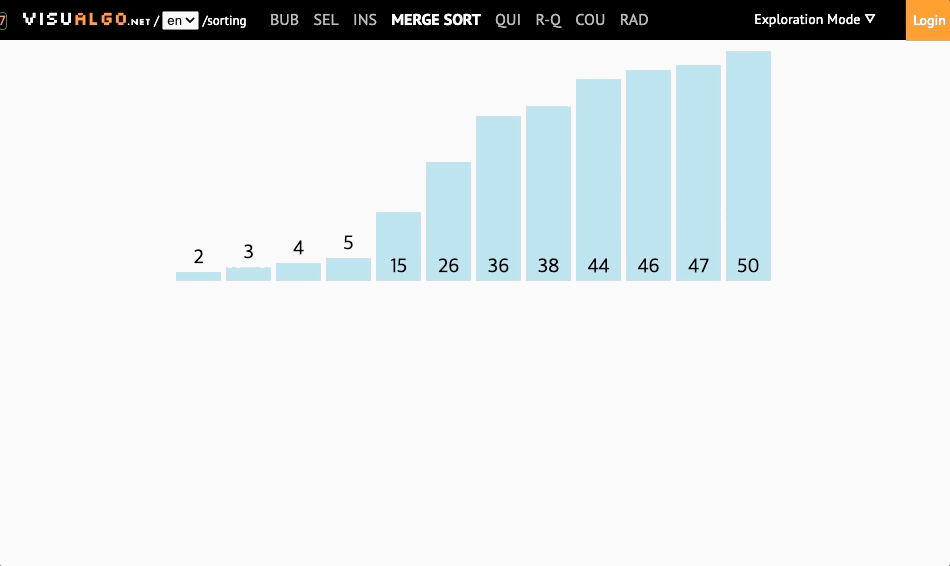
- 복잡하지만 효율적인 알고리즘 (분할 정복 알고리즘)
- 배열을 가운데 기준으로 분할한 뒤에 병합하여 정렬함
(배열이 더이상 쪼개지지 않을때까지 반으로 쪼갬 //원소가 하나남을때까지) - 재귀를 사용한 분할정복이라는 알고리즘 디자인기법에 근거하여 복잡한 문제를 복잡하지 않은 문제로 분할하여 정복하는 방식을 택함
- 병합정렬은 분할보다는 병합과정에서 정렬이 이루어진다.
function merge(array1, array2) {
const result = [];
let i = 0;
let j = 0;
while (i < array1.length && j < array2.length) {
if (array1[i] < array2[j]) {
result.push(array1[i]);
i++;
} else {
result.push(array2[j]);
j++;
}
}
if (i === array1.length) return result.concat(array2.slice(j));
if (j === array2.length) return result.concat(array1.slice(i));
}
function mergeSort(arr) {
if (arr.length <= 1) return arr;
let mid = Math.floor(arr.length / 2);
let left = mergeSort(arr.slice(0, mid)); // 재귀
let right = mergeSort(arr.slice(mid)); // 재귀
return merge(left, right); // 정렬된 두 배열을 정렬하여 합쳐주는 헬퍼 함수 사용
}
console.log(mergeSort([8, 3, 2, 7, 1, 5, 6, 4])); // [1,2,3,4,5,6,7,8]
병합정렬에서는 크게 두가지 과정을 볼 수 있다.
첫번째는 분할과정이고 두번째는 병합과정이다.
- 분할과정은 정말 쉽게 가운데 값을 통해서 분할을 한다.
- 분할될 요소가 하나 이상인지 확인하고 중간 인덱스를 뽑아준다.
- 재귀를 이용하여 분할하여 재귀가 다 돌고나면 두 영역을 병합시켜준다.
- 병합과정은 두개의 분할된 양쪽 배열에서 가장 작은 값을 하나씩 비교해서 더 작은 값을 먼저 넣는 방식으로 이루어진다.
- 영역별 인덱스와 병합한 결과를 담을 배열과 인덱스를 선언해준다.
- 병합할 두 영역의 데이터를 비교해준다.
- 비교후, 두 영역중 남은 숫자를 대입해주고 마지막으로 결과를 복사해주는 방식으로 동작한다.
병합정렬 특징과 시간복잡도
- 장점: 데이터 분포의 영향을 덜 받는다. //안정한 알고리즘
(퀵 정렬과는 달리 기준값을 설정하는 과정없이 중간에 둠으로써 입력데이터가 무엇이든 간에 정렬되는 시간을 동일하다고 볼 수 있게됨)
성능이 데이터 분포에 영향을 덜 받음,
Linked List를 이용하면 제자리 정렬이 가능 - 단점: 요소를 배열로 구성하면 임시 배열이 필요하다.
(정렬을 위한 추가 메모리가 필요해진다.) - 시간 복잡도: 최악,평균,최선 = O(n * logn)
- 파티션이 낱개가 될 때까지 쪼개야 하므로 n, 한번 호출당 검색해야할 데이터의 양이 절반씩 줄어드므로 logn를 가진다.
- 물리적으로 가운데 값을 파티션으로 나누므로 최악의 경우에도 O(nlogn)의 시간이 들게 된다.
📌 퀵 정렬(Quick Sort)

- 복잡하지만 효율적인 알고리즘
- 분할 정복 알고리즘
- 특정요소를 기준점(pivot)으로 잡고, 기준점보다 작은 요소는 왼쪽으로 기준점보다 큰 요소는 오른쪽으로 두고 왼쪽과 오른쪽을 각각 정복하는 방식
- 다른 정렬 알고리즘보다 효율적이고 빨라 퀵 정렬이라고 한다.
- 병합정렬과의 차이점은 병합정렬은 중앙을 기준으로 분할하기때문에 양쪽 개수가 거의 균등한 균등 분할이 일어나지만 퀵 정렬의 경우 임의의 피봇을 정하기 때문에 자신보다 작은 값이 많을 수도 큰 값이 많을 수도 있는 비균등 분할이 일어나게 된다.
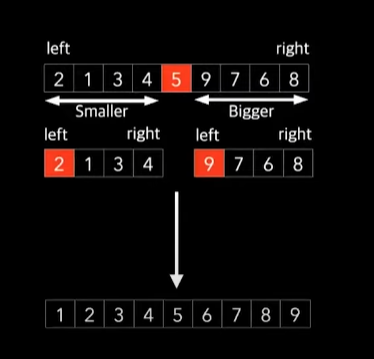
//피봇을 가장 왼쪽에둔 예시
- 피봇을 잡고 왼쪽엔 작은값, 오른쪽엔 큰값을 가지도록 정렬한다.
- 정렬한 후에 피봇을 기준으로 왼쪽과 오른쪽으로 분할하고, 각각 다시 퀵정렬을 사용하여 정복하는 방식
function pivot(arr, start = 0, end = arr.length - 1) {
const swap = (arr, idx1, idx2) => {
[arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]];
};
// 피봇이 항상 첫 번째 요소라고 가정
let pivot = arr[start];
let swapIdx = start;
for (let i = start + 1; i <= end; i++) {
if (pivot > arr[i]) {
swapIdx++;
swap(arr, swapIdx, i);
}
}
swap(arr, start, swapIdx);
return swapIdx;
}
console.log(pivot([4, 8, 2, 1, 5, 7, 6, 3]));
function quickSort(arr, left = 0, right = arr.length - 1) {
if (left < right) {
let pivotIndex = pivot(arr, left, right); // 위에서 정의한 헬퍼 함수 사용
// left
quickSort(arr, left, pivotIndex - 1);
// right
quickSort(arr, pivotIndex + 1, right);
}
return arr;
}- 병합정렬과 동일하게 우선 분할된 요소가 하나 이상인지 확인한 후 분할된 파티션의 첫 인덱스부터 마지막 인덱스까지의 파티션을 정렬하는 메서드를 호출한다.
(다음 분할을 위한 기준점도 반환해주어야 한다.) - 반환받은 기준점을 바탕으로 왼쪽 영역과 오른쪽 영역을 재귀호출한다.
- 파티션을 정렬하고 기준점을 반환해주는 메서드를 구현해야한다.
- 파티션에서 초기 피봇과 관련된 설정을 해주고 초기화된 low와 high가 교차되지 않을때까지 피봇보다 큰 값과 작은 값을 찾고 서로 교환해준다.
- 마지막으로 피봇과 high를 교환하고 high를 리턴한다.
퀵 정렬 특징과 시간복잡도
- 장점: 평균 실행시간이 다른 알고리즘보다 빠른 편이다.
(일반적으로 가장 빠른 정렬 알고리즘)
교환에 있어서 공간이 따로 필요없기 때문에 공간복잡도가 우수함 - 단점: Pivot에 따라서 성능차이가 심해진다.
불안정한 정렬 알고리즘
이미 정렬된 배열에 적용하면 최악의 시간복잡도가 나옴 - 시간 복잡도: 최악 O(n^2), 평균,최선 O(n * logn)
- 퀵 정렬은 피봇이 중간에 가까운 값을 찾을수록 성능이 좋아진다.
(피봇을 계속해서 제일 작은 값이나 제일 큰 값을 계속해서 찾게된다면 둘로 나뉘는 횟수가 n이되고 매 단계별 비교 연산의 횟수가 약 n이므로 O(n^2)까지 나올 수 있게된다.) - 피봇으로 중간에 가까운 값을 찾는다면 둘로 나뉘는 횟수가 logn, 매 단계별 비교연산의 횟수가 약 n이므로 O(nlogn)이 나옴
- 퀵 정렬은 피봇이 중간에 가까운 값을 찾을수록 성능이 좋아진다.
📌 자바스크립트에서의 sort
arr.sort([compareFunc]);원시타입을 정렬할때
- Dual Pivot Quick Sort를 사용한다. (피봇을 2개로 나눠서 정렬하는 알고리즘 = 구간이 3개로 나누어짐)
- 피봇을 하나만 쓰는 것보다 일반적으로 빠르다
Object타입을 정렬할때
- Tim Sort를 사용한다. (삽입정렬과 병합정렬의 하이브리드한 형태)
- Binary Insertion Sort를 사용 (삽입정렬 중에서도 2진삽입을 사용함)
- 2진삽입: 자기가 삽입될 곳을 찾을 때 이미 앞쪽에 정렬이 되어 있기때문에 이분탐색으로 자신의 위치를 찾을 수 있는 알고리즘
- 방식은 병합정렬과 같이 분할을 진행하다가 특정한 기준보다 작은 사이즈가 되면 분리를 멈춘후, 2진삽입정렬을 이용함, 그 다음 그 배열들을 가지고 특정 병합 조건에 맞게 병합함
- O(n * logn) 정렬 알고리즘의 단점을 최대한 극복한 알고리즘으로, Java와 Python에서도 사용된다.
📌 삽입정렬의 활용 문제

function solution(size, arr) {
let answer = [];
arr.forEach((x) => {
let pos = -1;
for (let i = 0; i < size; i++) {
if (x === answer[i]) pos = i;
}
if (pos === -1) {
answer.unshift(x);
if (answer.length > size) answer.pop();
}
else {
answer.splice(pos, 1);
answer.unshift(x);
}
})
return answer;
}
const arr = [1, 2, 3, 2, 6, 2, 3, 5, 7];
console.log(solution(5, arr));📌 정렬알고리즘 선택시 고려해야할 사항
1. 시간복잡도가 전부가 아니다.
- 상황에 맞는 알고리즘을 선택하는 것이 가장 좋음, 각각의 장단점이 있기때문
ex. 정렬 후 동일 키에 대한 상대적인 순서를 보장하고 싶은 경우
- 안정성이 보장된 알고리즘을 선택해야 함
- 안정성이 있는 알고리즘: 버블, 삽입, 병합
- 안정성이 보장되지 않은 알고리즘: 선택, 퀵(안정판이 존재하긴함), 힙
2. 공간복잡도를 고려해야 한다.
- 상황에 따라 메모리 사용량이 중요할 땐 공간복잡도를 고려해야함
- 1 : 버블, 삽입, 선택, 힙
- n : 병합
- logn : 퀵
- 이외에도 병합정렬과 퀵 정렬의 차이점 중 하나인 캐시와 관련된 지역성
- 키 값들의 분포 상태
- 데이터의 양
- 초기 데이터의 배열상태
- 사용 컴퓨터 시스템의 특성 등등...
참고자료
https://www.youtube.com/watch?v=ww6URL1l1ho&list=PLgXGHBqgT2TvpJ_p9L_yZKPifgdBOzdVH&index=128&t=283s
https://velog.io/@young_mason/dd
https://velog.io/@jangws/11.-%ED%80%B5-%EC%A0%95%EB%A0%ACQuick-Sort-JS
https://www.youtube.com/watch?v=8c-Q8anmJcM&list=PLgXGHBqgT2TvpJ_p9L_yZKPifgdBOzdVH&index=21
