[NLP] RNN (Recurrent Neural Net), gradient vanishing/exploding 현상과 long-term dependency 문제

nkw011·2022년 7월 18일

Natural Language Processing(NLP) 기초 내용, 실습, 논문 정리

목록 보기

2/15

1. RNN(Recurrent Neural Network)

sequence 데이터, timeseries 데이터를 처리하기 위한 모델. 핵심은 과거의 정보를 기억하고 이를 활용한다는 것이다. sequence 데이터, timeseries 데이터가 아니더라도 이전 정보(과거 정보)를 기억해 활용해야하는 데이터라면 RNN을 사용해 처리하는 것을 고려해봐도 좋을 것 같다. RNN을 이용해 처리할 수 있는 데이터를 대표적으로 sequence 데이터, timeseries 데이터를 꼽는 이유는 해당 데이터가 이전 정보를 활용해서 예측을 진행해야하는 경우가 많기 때문이다.

RNN이 과거의 정보를 기억할 수 있는 이유는 FFNN, CNN과 달리 모델 내부에서 계산된 결과값이 다시 다음 계산의 입력으로 들어가는 재귀적인(Recurrent) 특성이 있기 때문이다. RNN의 구조를 살펴보면서 이전에 계산된 결과가 다시 어떻게 활용이 되는지 살펴보자.

기본 구조

$x$ 는 입력층의 입력 벡터, $y$ 는 출력층의 출력 벡터이다. 파란 박스는 입력층과 출력층 사이에 존재하는 은닉층을 간단하게 표시한 것이다.

RNN도 기본적으로 입력을 이용해 출력값을 만드는 것은 똑같다.

입력을 $x_t$ , 출력을 $y_t$ 라고 적은 이유는 입력 데이터를 sequence 데이터로 가정했기 때문이다.
입력으로 들어오는 sequence 데이터의 길이를 $n$ 이라고 했을 때, $t$ 번째 데이터를 처리하는 것이라고 볼 수 있다.
일반적으로 sequence의 첫번째 원소를 1번째 시점(timestep)에 입력으로 들어오는 데이터, 두번째 원소를 2번째 시점(timestep)에 입력으로 들어오는 데이터라고 부른다. 이는 RNN이 sequence 데이터의 원소를 순서대로(시간 순대로) 처리하는 것에 기인한다. 따라서 $x_t$ 는 $t$ 시점에 들어오는 데이터라고 부르며 $t$ 시점을 기준으로 $x_{t-1}$ 을 이전 시점의 데이터, $x_{t+1}$ 을 다음 시점의 데이터라고 부른다. 순서를 시점으로 바꿔서 부른다고 생각하면 편하다.

하지만 다른 부분도 하나 존재하는데 바로 은닉층에 존재하는 화살표이다.

해당 화살표는 현재 시점의 은닉층의 결과값이 다음 시점 은닉층의 입력으로 들어가는 것을 뜻한다. 이렇게 전달되는 값을 은닉 상태(hidden state)∙은닉 상태 벡터(hidden state vector)라고 부르며 결국 다음 시점에 은닉층으로 들어오는 입력은 다음 시점의 입력 벡터와 현재 시점의 은닉 상태 벡터 총 2가지가 들어간다.

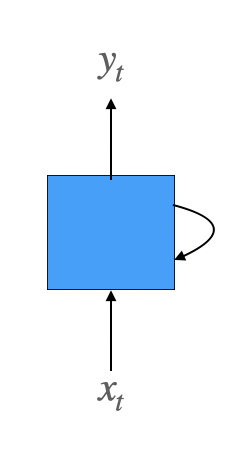
펼쳐서 보면 더 구조를 이해하기 쉽다.

각 시점마다 은닉층으로 현재 시점의 입력 벡터, 이전 시점의 은닉 상태 벡터가 들어오며 sequence 데이터를 모두 읽을 때까지 해당 구조가 반복되는 것을 알 수 있다.

은닉 상태 벡터를 $h$ 로 표시했다. 첫번째 시점에서는 이전 시점에 생산된 은닉 상태 벡터가 없기 때문에 $h_0$ 라는 일종의 더미값을 준 것이라고 보면 된다.
그림으로 인해 헷갈릴 수 있는데 여기서 주의할 점은 각 시점마다 다른 모델이 사용되는 것이 아니다. 동일한 모델(동일한 학습 파라미터)이 사용되는 것이며 이해를 위해 하나의 모델을 각 시점마다 반복된 형태로 그려놓은 것으로 보면된다.

따라서 은닉층에서는 이전 시점의 은닉 상태 벡터가 들어오고 이를 이용해 다시 현재 시점의 은닉 상태 벡터를 만들기 때문에 은닉층이 일종의 메모리 역할을 수행한다고 볼 수 있으며 이를 통해 이전 정보를 기억할 수있게된다.

은닉 상태 벡터에 정보가 저장이 된다고 볼 수 있다.

어떤 방식으로 은닉 상태 벡터를 활용하는지 살펴 보자. (이제부터 입력 벡터를 input vector, 은닉 상태 벡터를 hidden state vector, 출력 벡터를 output vector로 표기하겠다.)

hidden state vector(은닉 상태 벡터) 만들기

현재 시점의 hidden state vector를 만들기 위해 2가지 벡터가 필요하다고 했다.

$x_t$ : 현재 시점의 input vector
$h_{t-1}$ : 이전 시점의 hidden state vector

RNN 모델에서 사용되는 파라미터를 $W$ 로 설정하고 이를 활용해 계산하는 함수를 $f_W$ 라고 하겠다.

현재 시점의 hidden state vector는 다음과 같이 계산이 된다.

$h_t = f_W(h_{t-1}, x_t)$

이를 좀 더 자세히 풀어보면 다음과 같다.

$h_t = tanh(W[x_t, h_{t-1}])$ , ( $[x_t, h_{t-1}]$ 은 두 벡터를 concatenation한 것을 뜻한다. )

hidden state vector를 2차원 벡터, input vector를 3차원이라고 가정했을 때 $W[x_t, h_{t-1}]$ 에서 일어나는 일을 그림으로 살펴보면 다음과 같다.

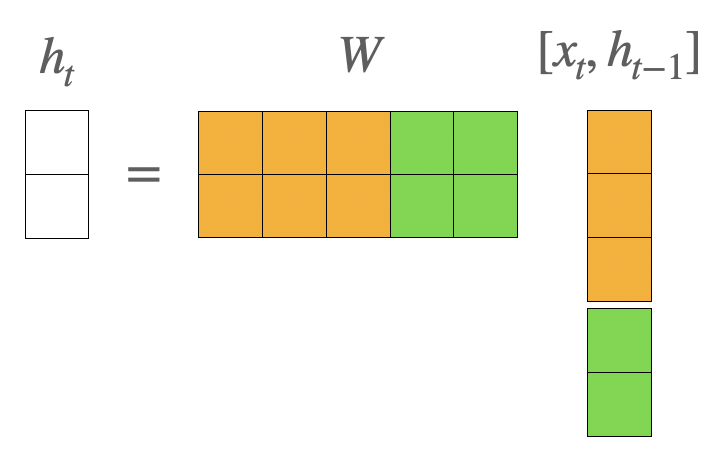
$W$ 의 행벡터가 concatenation한 vector와 내적 연산을 하여 현재 시점의 hidden state vector를 만드는 것을 알 수 있다..

$h$ 가 2차원 벡터이고 $[x,h]$ 가 5차원 벡터이기 때문에 $W: 2 \times 5$ 행렬이 된다.

위 그림을 더 자세히 살펴보면 $W$ 의 1~3번째 열까지는 input vector와 내적 계산이 되고, 4~5번째 열까지는 hidden state vector와 내적 계산이 되어 두 계산 결과가 합해지는 것으로 볼 수있다.

따라서 W를 2개의 행렬로 분리해 다음과 같은 방법으로 표기를 더 많이 한다.

$h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t)$
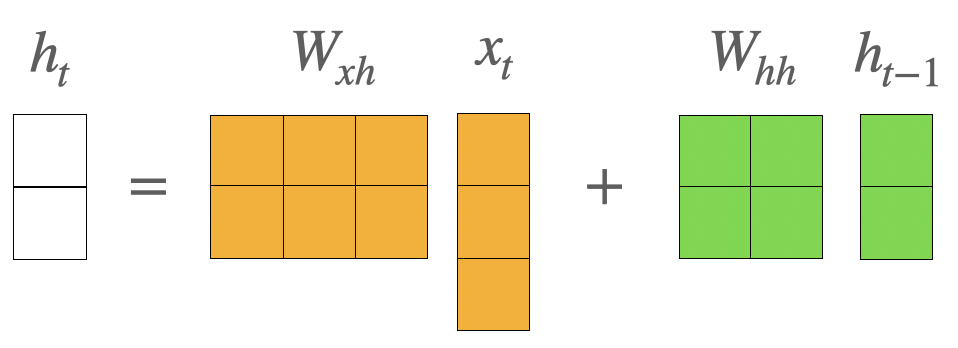
$W_{hh}: 2 \times 2$ 행렬, 결국 $h_{t-1} \rightarrow h_t$ 로 선형변환한다고 볼 수 있다.
$W_{xh}: 2 \times 3$ 행렬, 결국 $x_t \rightarrow h_t$ 로 선형변환한다고 볼 수 있다.

두 행렬 곱의 합을 통해 나온 결과가 activation fucntion으로 사용되는 non-linear function인 $tanh$ 를 통과해서 현재 시점의 hidden state vector인 $h_t$ 가 만들어진다.

(bias term은 따로 표기하지 않았다.)

output vector(출력 벡터) 만들기

현재 시점의 output vector로 hidden state vector를 그대로 활용하는 경우도 있지만 보통 hidden state vector를 다시 한 번 선형변환을 해서 사용한다.

$y_t = f(W_oh_t)$

$f$ 는 non-linear function으로 상황에 따라 적절한 것을 적용하면 된다. 이진 분류 시에는 cross-entropy 함수를 적용할 수 있고 다중 분류 시에는 softmax 함수를 사용할 수 있다. (bias term은 따로 표기하지 않았다.)

2. RNN의 여러 형태

앞서 RNN이 sequence 데이터, timeseries 데이터에 자주 쓰인다고 언급했다.(이전 정보를 기억해야하는 데이터라면 어떤 형태이던지 상관이 없지만…)

입력이 sequence의 형태의 데이터로 들어오다 보니 출력 역시 sequence 형태의 데이터가 된다.

RNN은 입력과 출력의 sequence 길이에 따라 여러 형태로 나눌 수 있다.

one-to-one

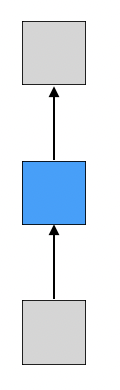
일반적인 Neural Network와 구조가 동일하다.

한 번에 입력을 받고 한 번에 출력하기 때문에 (non-sequence to non-sequence로 볼 수 있다.)

one-to-many

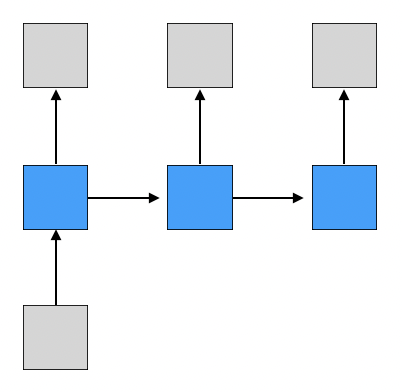
한 번에 입력을 받고 sequence 데이터를 출력하는 형태이다. (non-sequence to sequence)

RNN은 매 시점마다 입력을 받기 때문에 구현할 때 두번째 시점부터는 더미 데이터를 입력으로 넣어주어야한다.

대표적으로 image captioning이 존재한다.

image captioning: 주어진 image에 대한 설명글을 만드는 작업

many-to-one

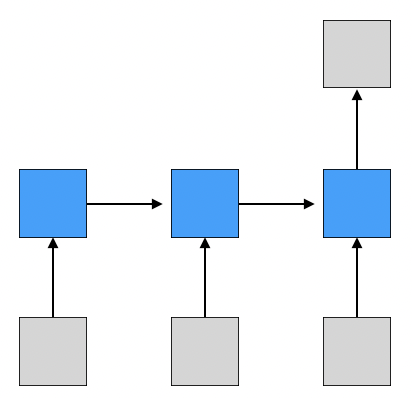
sequence를 입력 받고 하나의 값을 출력하는 형태이다.

대표적으로 sentiment classification이 존재한다.

sentiment classification: 감정 분류(positive or negative)

many-to-many

sequence를 입력 받고 sequence를 출력하는 형태이다.

many-to-many는 다시 2가지로 분류할 수 있다.

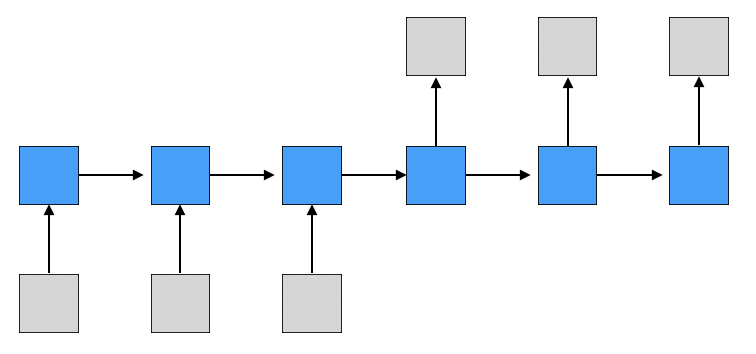
첫번째 형태는 입력 문장을 모두 읽고 나서 출력을 하는 형태이다. (출력할 때는 입력 값이 들어오지 않는다.)

대표적으로 machine translation이 존재한다.

machine translation: 기계 번역

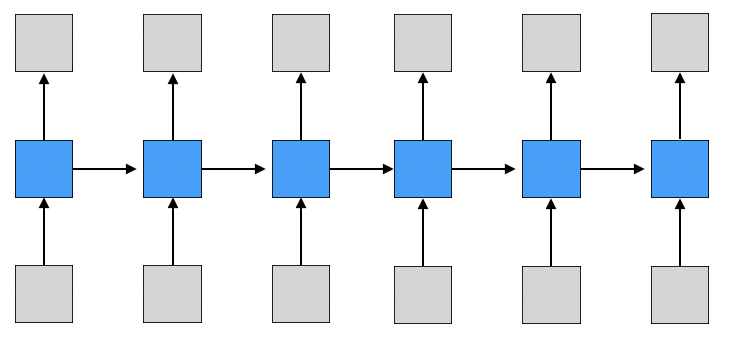
두번째 형태는 매 시점마다 입력이 들어오고 입력이 주어질 때마다 출력을 내보내는 형태이다.

대표적으로 video classification of frame level이 존재한다.

3. BPTT (Backpropagation through time)

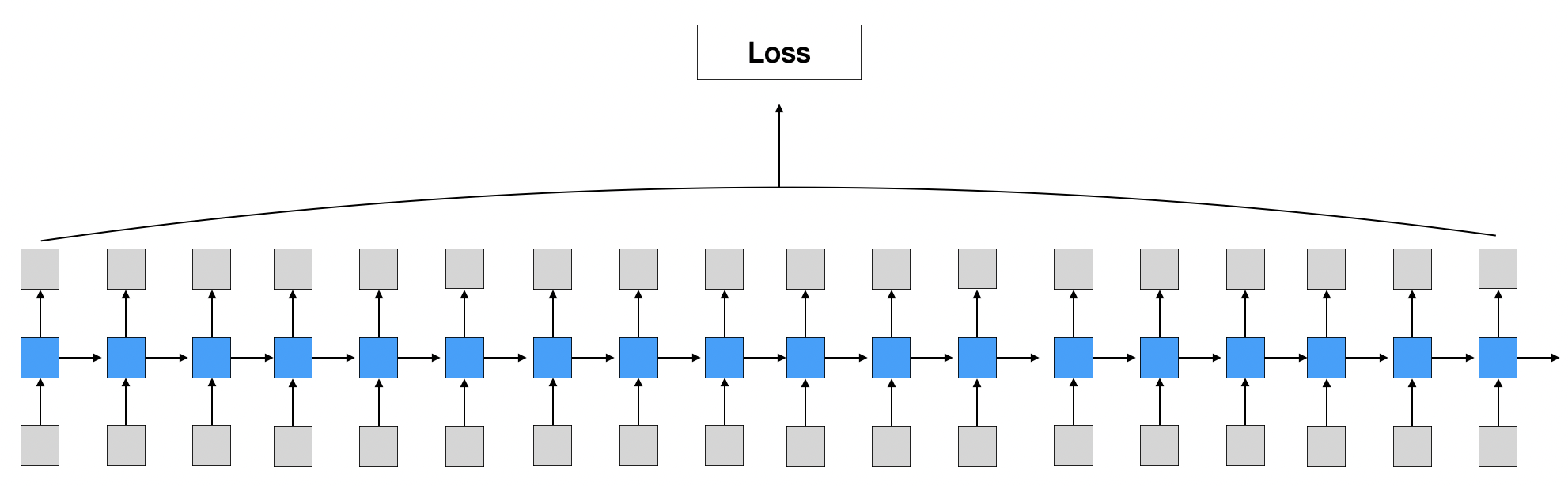
RNN 구조의 특성상 전체 sequence를 모두 읽은 이후 출력값을 계산하고 이에 따라 역전파가 이루어지는 형태이기 때문에 sequence가 많거나 길수록 시간이 오래 걸린다.

시간이 오래 걸리는 이유는 각 시점에서 gradient를 계산할 때 이전 모든 시점까지 gradient가 전달되어 계산되어져야하기 때문이다.
자세한 내용은 참고를 확인하면 역전파 계산과 함께 자세한 수식을 살펴볼 수 있다.

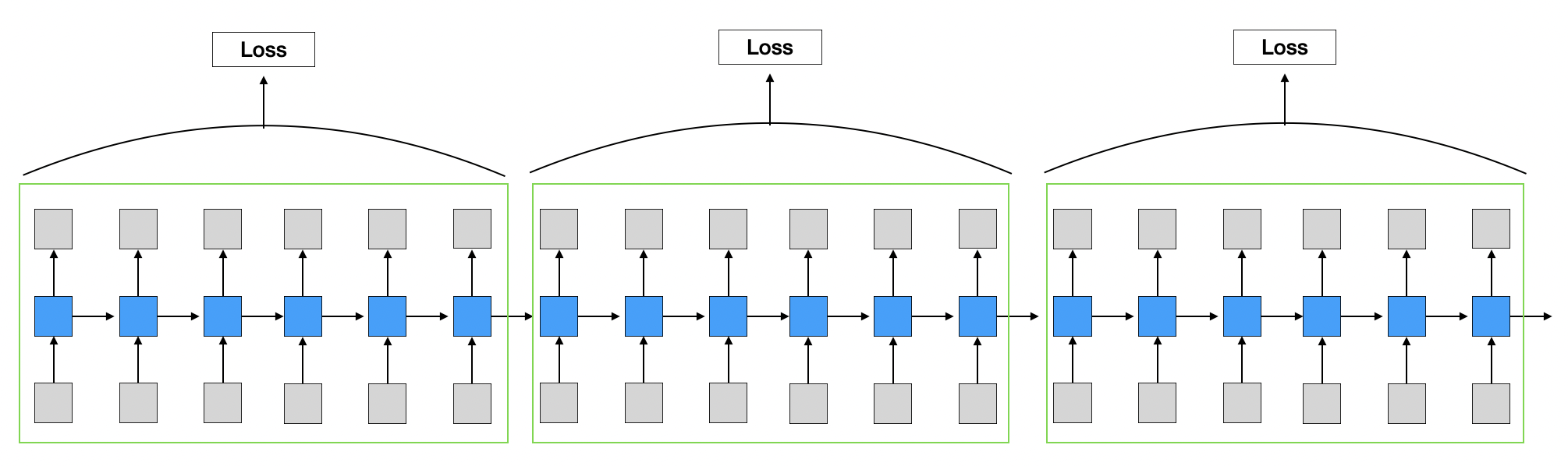
따라서 sequence를 일정 단위로 나누어 역전파를 수행한다.

순전파할 때는 일정 단위에 상관에 없이 이전 시점의 hidden state vector가 다음 시점으로 들어가는 형태로 연속적으로 수행된다.
역전파할 때는 일정 단위로 끊어서 계산이 수행된다.

4. Vanishing/Exploding Gradient Problem in RNN

RNN에서 일어나는 역전파 과정을 자세히 살펴보면 동일한 행렬( $W_{hh})$ 이 반복적으로 곱해지는 것을 알 수 있다.

같은 값이 계속해서 곱해지기 때문에 등비수열의 효과를 일으키는데 이 때 행렬의 특잇값이 1보다 크면 gradient가 지수적으로 증가하고 1보다 작으면 gradient가 지수적으로 작아질 수가 있다.

모델 학습은 모델 파라미터에 계산된 gradient를 적용하여 갱신하는 형태로 이루어지기 때문에 gradient가 지수적으로 증가하게되면 오버플로우 현상을 일으킬 수 있고 반대로 gradient가 지수적으로 작아지게되면 gradient가 0이 되어 모델 파라미터가 갱신이 되지 않는 현상이 발생할 수 있다. 이를 gradinet exploding(기울기 폭발), gradient vanishing(기울기 소실) 현상이라고 한다.

이런 구조적인 특성 외에도 RNN에 사용되는 $tanh$ 함수 또한 gradient vanishing 현상에 영향을 줄 수 있다. ( $tanh$ 함수의 기울기 최댓값이 1 이기 때문이다.)

따라서 sequence의 길이가 길수록 동일한 행렬( $W_{hh})$ 이 반복적으로 곱해지기 때문에 gradient exploding/vanishing 현상에 크게 영향을 받아 모델 학습이 이루어지지 않기 때문에 long-term dependency problem이 발생한다는 단점이 존재한다. 이는 결국 sequence의 길이가 길수록 RNN이 기억할 수 있는 정보가 많지 않게 된다는 것을 의미한다. (기억력에 영향을 준다.)

Long-Term Dependency Problem

다음과 같은 예시 문장이 있다고 가정해보자.

“영국으로 축구 여행을 떠났어. 첫째날에는 북런던에 있는 토트넘의 경기를 봤어. 둘째날에는 맨체스터에 있는 맨체스터 유나이티드 경기를 봤어. 셋째날에는 다시 런던으로 가서 첼시 경기를 봤어. 일주일 여행을 마친뒤 귀국해서 친구들과 얘기를 나눴는데 친구가 첫째날에 어떤 경기를 봤냐고 물어보는거야. 첫째날에 어떤 구단의 경기를 봤냐면 ? 구단의 경기를 봤어.”

‘?’ 위치에 들어가야할 적절한 말은 ‘토트넘’이다. ‘토트넘’의 위치와 ‘?’ 위치는 멀리 떨어져있지만(long term) 서로 연관(의존성, dependency)이 되어있다. RNN은 sequence의 길이가 길수록 gradient exploding 또는 gradient vanishing 현상으로 인해 매우 긴 문장 또는 문단 사이의 정보를 온전히 기억하지 못하고 정보를 소실할 수 있다.

이러한 문제를 long-term dependency problem이라고 한다.