[algorithm] 0-1 BFS

소개

0-1 BFS는 가중치가 0, 1로 주어진 그래프에서 최단경로를 찾아낼 수 있는 알고리즘입니다. 최단경로 알고리즘에는 다익스트라 알고리즘을 사용할 수 있지만, 시간 복잡도가 $O({E} log{E})$ 또는 $O({E}log{V})$인 반면에, 0-1 BFS는 $O(V + E)$의 시간 복잡도로 문제를 해결할 수 있습니다.

일반적인 BFS 탐색과 동일하지만, 가중치가 0인 정점이 존재하기 때문에 실제로 정점의 방문 횟수가 더 많더라도 가중치가 더 낮은 경우를 고려해야합니다. 그렇기 때문에 결과 값이 방문 횟수의 최소가 아닌 가중치의 최소인 경우를 찾기 위해서는 가중치가 낮은 경로부터 탐색해야합니다.

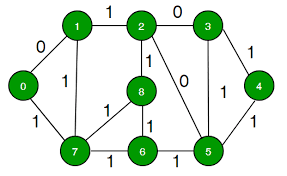
정점 1에서 정점 2로의 이동 = 방문 횟수 1, 가중치 1
정점 1에서 정점 3, 4를 거쳐 정점 2로의 이동 = 방문 횟수 3, 가중치 0

가중치가 낮은 정점으로의 이동을 높은 우선 순위로 해야하기 때문에, 덱의 가장 앞단(front)에 삽입합니다. BFS와 동일하게 간선의 갯수(E)만큼 탐색을 하게되고, 정점의 갯수(V)만큼 중복없이 방문하기 때문에 시간 복잡도는 $O(V + E)$로 동일합니다.

예제

https://www.acmicpc.net/problem/13549

import java.io.*;
import java.util.Arrays;
import java.util.LinkedList;

public class Main {

    public static int[] check;

    public static void main(String[] args) throws IOException {
        try (BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
             BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out))) {
            String[] s = reader.readLine().split(" ");
            int n = Integer.parseInt(s[0]);
            int k = Integer.parseInt(s[1]);
            check = new int[100001];
            Arrays.fill(check, -1);

            bfs(n, k);
            writer.write(check[k] + "");
        }
    }

    public static void bfs(int n, int k) {
        LinkedList<Integer> queue = new LinkedList<>(); // deque
        queue.offer(n);
        check[n] = 0;

        while (!queue.isEmpty()) {
            int position = queue.poll();

            if (position == k) {
                return;
            }

            if (position * 2 <= 100000 && check[position * 2] == -1) {
                queue.addFirst(position * 2); // 높은 우선순위
                check[position * 2] = check[position];
            }

            if (position > 0 && check[position - 1] == -1) {
                queue.offer(position - 1);
                check[position - 1] = check[position] + 1;
            }

            if (position < 100000 && check[position + 1] == -1) {
                queue.offer(position + 1);
                check[position + 1] = check[position] + 1;
            }
        }
    }

}

현재 정점(x)에서 2배만큼의 정점(2x)으로 이동하는 가중치는 0입니다. 다른 정점으로의 이동(-1 or +1)보다 가중치가 낮으므로 우선 순위가 높아야하기 때문에 덱의 가장 앞단(front)에 삽입하여 문제를 해결할 수 있습니다.

https://www.acmicpc.net/problem/1261

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;

public class Main {

    public static int[][] graph;

    public static int[] dx = {-1, 0, 1, 0};

    public static int[] dy = {0, 1, 0, -1};

    public static void main(String[] args) throws IOException {
        try (BufferedReader reader = new BufferedReader(new InputStreamReader(System.in))) {
            String[] s = reader.readLine().split(" ");
            int n = Integer.parseInt(s[0]);
            int m = Integer.parseInt(s[1]);
            graph = new int[m][n];

            for (int i = 0; i < m; i++) {
                String line = reader.readLine();
                for (int j = 0; j < n; j++) {
                    graph[i][j] = Character.getNumericValue(line.charAt(j));
                }
            }

            bfs();
        }
    }

    public static void bfs() {
        LinkedList<int[]> queue = new LinkedList<>(); // deque
        queue.offer(new int[]{0, 0, 0});
        graph[0][0] = -1;

        while (!queue.isEmpty()) {
            int[] poll = queue.poll();
            int x = poll[0];
            int y = poll[1];
            int c = poll[2];

            if (x == graph.length - 1 && y == graph[0].length - 1) {
                System.out.println(c);
                return;
            }

            for (int i = 0; i < dx.length; i++) {
                int nx = x + dx[i];
                int ny = y + dy[i];

                if (nx < 0 || ny < 0 || nx >= graph.length || ny >= graph[0].length) {
                    continue;
                }

                if (graph[nx][ny] == 0) { // 방
                    queue.addFirst(new int[]{nx, ny, c}); // 높은 우선순위
                } else if (graph[nx][ny] == 1) { // 벽
                    queue.offer(new int[]{nx, ny, c + 1});
                }

                graph[nx][ny] = -1; // 방문 처리
            }
        }
    }

}

벽(1)을 부수고 이동하는 경우는 가중치가 1만큼 증가하지만 방(0)으로 이동하는 경우는 가중치는 0입니다. 방으로 이동하는 것이 벽으로 이동하는 것보다 가중치가 낮으므로 우선 순위가 높아야하기 때문에 덱의 가장 앞단(front)에 삽입하여 문제를 해결할 수 있습니다.